Duocylinder (EntityTopic, 14)
From Hi.gher. Space
A duocylinder is the Cartesian product of two circles, and is therefore the square of the circle. It is also the limit of the set of m,n-duoprisms as m and n tend to infinity.
Equations
- Variables:
a ⇒ radius of the circle in the xy plane
b ⇒ radius of the circle in the zw plane
- All points (x, y, z, w) that lie on the sole 2D face of a duocylinder will satisfy the following equations:
x2 + y2 = a2
z2 + w2 = b2
- A duocylinder has two cells which meet at the 2D face. These are given respectively by the systems of equations:
- x2 + y2 = a2; z2 + w2 ≤ b2
- x2 + y2 ≤ a2; z2 + w2 = b2
- Each of these bounding volumes are topologically equivalent to the inside of a 3D torus. The set of points (w,x,y,z) that satisfy either the first or the second set of equations constitute the surface of the duocylinder.
- The hypervolumes of a duocylinder are given by:
total surface area = 4π2ab
surcell volume = 2π2ab(a + b)
bulk = π2a2b2
- The realmic cross-sections (n) of a duocylinder are cylinders of varying heights.
Net
The net of a duocylinder is two touching cylinders which have the length equal 2πr.
Cross-sections
Blue disk-first:
 Red disk-first:
Red disk-first:
 Face-first:
Face-first:

Projection
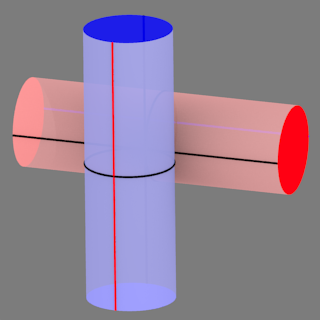
The perspective projection of a duocylinder is the following shape. The purple part is one cell, and the black part is the other cell.
In a parallel projection, both cells collapse to cylinders, one capped and one uncapped, resulting in a single cylinder being observed as the projection.
| Notable Tetrashapes | |
| Regular: | pyrochoron • aerochoron • geochoron • xylochoron • hydrochoron • cosmochoron |
| Powertopes: | triangular octagoltriate • square octagoltriate • hexagonal octagoltriate • octagonal octagoltriate |
| Circular: | glome • cubinder • duocylinder • spherinder • sphone • cylindrone • dicone • coninder |
| Torii: | tiger • torisphere • spheritorus • torinder • ditorus |
| 13. 31 Spherinder | 14. 22 Duocylinder | 15. 211 Cubinder |
| List of tapertopes | ||
| 5a. (II)II Cubinder | 5b. ((II)II) Spheritorus | 6a. (II)(II) Duocylinder | 6b. ((II)(II)) Tiger | 7a. (III)I Spherinder | 7b. ((III)I) Torisphere |
| List of toratopes | |||||
| 27. (<(II)I>I) Biconic crind | 28. [(II)(II)] Duocylinder | 29. <(II)(II)> Duocircular tegum |
| List of bracketopes | ||