Coninder (EntityTopic, 11)
From Hi.gher. Space
A coninder is a special case of a prism where the base is a cone. It is bounded by two cones, a cylinder and a cylindrogram.
Equations
- Variables:
r ⇒ radius of base of coninder
h ⇒ height of coninder
l ⇒ length of coninder
- The hypervolumes of a coninder are given by:
total edge length = 4πr + l
total surface area = 2πr(r + 2l + √(r2 + h2))
surcell volume = πr(2rh∕3 + l(r + √(r2 + h2)))
bulk = π∕3 · r2hl
- The realmic cross-sections (n) of a coninder are:
[!x,!y] ⇒ isosceles triangular prism of base length 2r, perpendicular height h and length l
[!z] ⇒ cylinder of radius (r − nr∕h) and height l
[!w] ⇒ cone of base radius r and height h
Cross-sections
Cylinder-first:
 Cone-first:
Cone-first:
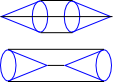
 Round face-first:
Round face-first:

Projections
The following is the parallel projection of the coninder:
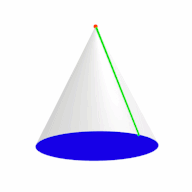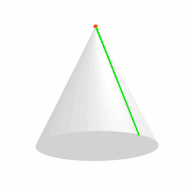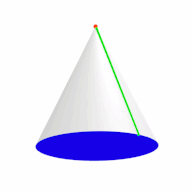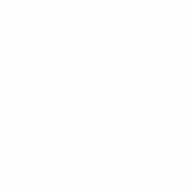
In perspective projection, the coninder can also appear as two concentric cones. Note that the frustum at the bottom is actually a cylinder:
The following are also perspective projections of the coninder. It shows the two cones and the cylinder, with the cylindrogram collapsed into a line:
Its edge-first projection into 3-space is a cylinder containing two cones joined apex to apex by an edge.
| Notable Tetrashapes | |
| Regular: | pyrochoron • aerochoron • geochoron • xylochoron • hydrochoron • cosmochoron |
| Powertopes: | triangular octagoltriate • square octagoltriate • hexagonal octagoltriate • octagonal octagoltriate |
| Circular: | glome • cubinder • duocylinder • spherinder • sphone • cylindrone • dicone • coninder |
| Torii: | tiger • torisphere • spheritorus • torinder • ditorus |
| 23. [11]2 Square dipyramid | 24. 121 Coninder | 25. 1[11]1 Square pyramid prism |
| List of tapertopes | ||