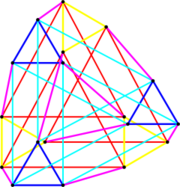
Triangular octagoltriate (EntityTopic, 11)
From Hi.gher. Space
The triangular octagoltriate is a powertope formed by taking the octagon of the triangle. It is therefore the convex hull of two ditriangular duoprisms, each being the duoprism of triangles of side 1 and 1+√2, oriented in opposite axes.
Cells
The triangular octagoltriate has the following cells:
- 6× prism of side 1+√2 and end equilateral triangle of side 1
- 9× antifrustoid of base rectangle of sides 1 and 1+√2 and unknown height
Faces
The triangular octagoltriate has the following faces:
- 6× equilateral triangle of side 1
- 18× rectangle of sides 1 and 1+√2
- 18× trapezium of base 1+√2, height √3 and apex ½√6+√3
Incidence matrix
Dual: (dual of triangular octagoltriate)
| # | TXID | Va | Ea | Eb | Ec | 3a | 4a | 4b | C1a | C2a | Type | Name |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Va | = point | ; | |||||||||
| 1 | Ea | 2 | = digon | ; edges on small triangles | ||||||||
| 2 | Eb | 2 | = digon | ; edges on large (internal) triangles | ||||||||
| 3 | Ec | 2 | = digon | ; edges joining small to large | ||||||||
| 4 | 3a | 3 | 3 | 0 | 0 | = triangle | ; small triangles | |||||
| 5 | 4a | 4 | 2 | 2 | 0 | = square | ; rectangles in prisms | |||||
| 6 | 4b | 4 | 1 | 1 | 2 | = square | ; trapeziums in antifrustoids | |||||
| 7 | C1a | 6 | 6 | 3 | 0 | 2 | 3 | 0 | = triangular prism | ; prisms | ||
| 8 | C2a | 8 | 4 | 4 | 4 | 0 | 2 | 4 | = cube | ; antifrustoids | ||
| 9 | H4.1a | 18 | 18 | 18 | 9 | 6 | 18 | 18 | 6 | 9 | = triangular octagoltriate | ; |
Usage as facets
This polytope does not currently appear as facets in any higher-dimensional polytopes in the database.
| Notable Tetrashapes | |
| Regular: | pyrochoron • aerochoron • geochoron • xylochoron • hydrochoron • cosmochoron |
| Powertopes: | triangular octagoltriate • square octagoltriate • hexagonal octagoltriate • octagonal octagoltriate |
| Circular: | glome • cubinder • duocylinder • spherinder • sphone • cylindrone • dicone • coninder |
| Torii: | tiger • torisphere • spheritorus • torinder • ditorus |