Xylochoron (EntityTopic, 12)
From Hi.gher. Space
The xylochoron, also known as the icositetrachoron and the 24-cell, is a very unique object with special properties that is matched by no other polytope in any dimension.
- It is the only regular, convex, self-dual polytope that isn't also a simplex, besides regular polygons in 2D. A self-dual polytope is one where if you reverse the order of its elements, you get the same polytope. In all other dimensions above 2D, the only self-dual polytopes are the n-simplices: the tetrahedron, pentachoron, etc.
- It is the only regular, tessellating polytope that isn't a hypercube or cross polytope, besides the triangle and hexagon in 2D. This means that you can stack 24-cells together to tile a 4D region of space with no gaps in between. The hypercubes have this property: squares tile 2D space, cubes tile 3D space, and tesseracts tile 4D space. In 3D, the rhombic dodecahedron also has this property, but it is not a regular polytope.
- Its closest equivalents in 3D are the rhombic dodecahedron and the cuboctahedron. However, unlike the rhombic dodecahedron which has faces that are not regular polygons, and the cuboctahedron which has two different types of regular polygons for its faces, the cells of the 24-cell are all identical, regular octahedra.
The xylochoron is also the rectified aerochoron.
coordinates
When constructed as a combination of a tesseract with 8 cubic pyramids, the coordinates of the xylochoron with side 2 are all premutations of:
(±1, ±1, ±1, ±1)
(±2, 0, 0, 0)
When constructed as a rectified aerochoron, the coordinates are all permuatrions of:
(±√2, ±√2, 0, 0)
Equations
- The hypervolumes of an icositetrahedron with side length l are given by:
total edge length = 96l
total surface area = 24√3 · l2
surcell volume = 8√2 · l3
bulk = 2l4
Projection
Vertex-first projection
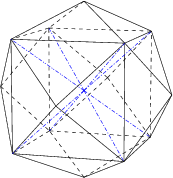
The vertex-first orthographic projection of the 24-cell has a rhombic dodecahedral envelope. The vertex is at the center of the envelope, and may be thought of as the "north pole" of the 24-cell. There are 6 octahedra (slightly flattened by the projection) packed around it in a cubic symmetry. These are the "northern cells". Each of the 12 faces of the rhombic dodecahedron corresponds with an octahedral cell viewed at from a 90-degree angle, hence they appear flat. These are the "equitorial cells". On the other "side" of these equitorial cells are another 6 cells arranged in cubic symmetry around the "south pole" vertex. These 6 cells would be hidden from view if a 4D viewer were looking at the 24-cell from this viewpoint. This makes a total of 24 cells.
The vertex-first perspective projection of the 24-cell has the same structure as described for the orthographic projection, except that due to foreshortening, its equitorial cells are not completely flat and so its envelope is a tetrakis hexahedron. The following diagram shows this perspective projection, with hidden cells omitted.
The blue edges lie inside the envelope, and meet at the “north pole” vertex.
Cell-first projection
The cell-first parallel projection of the 24-cell has a cuboctahedral envelope. The closest cell to the viewer lies in the center of this cuboctahedron, and its vertices touch the centers of the square faces of the cuboctahedron. Each triangular face of the central octahedron is in dual orientation with the triangular face of the cuboctahedron in the same octant. These pairs of triangles are actually opposite faces of octahedral cells, which appear in projection to be distorted to exactly fill the space between the central octahedron and the cuboctahedral envelope. There are 8 such pairs.
Furthermore, each square face of the cuboctahedron actually corresponds with an octahedral cell viewed at from a perpendicular angle, hence they appear as flat squares in projection. These 6 squares connect the outer half of the 24-cell containing the central octahedron and the 8 surrounding cells with another central octahedron and its 8 surrounding cells, which lie on the other side of the 24-cell in the 4th direction. Hence, there are 9 + 6 + 9 = 24 cells in total. These other 9 cells are hidden from view to a 4D viewer looking at the 24-cell from this viewpoint.
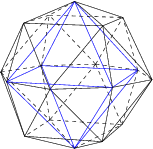
The cell-first perspective projection of the 24-cell has an envelope in the shape of a modified cuboctahedron, where the square faces are replaced by shallow pyramids. The layout of cells within the envelope are similar to that in the parallel projection. The following diagram shows this perspective projection, with hidden cells omitted:
The central cell is highlighted in blue. This is the cell closest to the 4D viewer.
Construction
One possible way to construct the icositetrachoron is by a process analogous to the construction of the rhombic dodecahedron in 3D. That is, by cutting a tesseract into 8 cubic pyramids and attaching them to the faces of a second, congruent tesseract. This construction is easiest to understand if one compares the cell-first projection of the tesseract and the vertex-first projections of the icositetrachoron.
Another construction is via the rectification of the hexadecachoron. This construction is easiest to understand if one compares the vertex-first projection of the hexadecachoron and the cell-first projection of the icositetrachoron.
Relation to other tetrashapes
If a 24-cell is truncated at a depth halfway to that which yields its dual, the bitruncated 24-cell is obtained. Since the 24-cell is self-dual, this bitruncate is cell-transitive.
If the vertices of a 24-cell inscribed in a 600-cell are removed from the 600-cell, the convex hull of the remaining vertices is the snub 24-cell. The snub 24-cell may also be obtained by truncating the 24-cell with the golden ratio such that icosahedral cells are formed in place of its 24 cells. Tetrahedral cells are introduced in the process.
The facet normals of the tesseract and the 16-cell, scaled to equal length, form the facet normals of the 24-cell.
If the 24-cell is bisected - halfway between one octahedral cell and the opposite cell - each half is the segmentotope K4.29, the octahedral semicupola.
Incidence matrix
Dual: Self-dual
| # | TXID | Va | Ea | 3a | C1a | Type | Name |
|---|---|---|---|---|---|---|---|
| 0 | Va | = point | ; | ||||
| 1 | Ea | 2 | = digon | ; | |||
| 2 | 3a | 3 | 3 | = triangle | ; | ||
| 3 | C1a | 6 | 12 | 8 | = octahedron | ; | |
| 4 | H4.1a | 24 | 96 | 96 | 24 | = xylochoron | ; |
Usage as facets
This polytope does not currently appear as facets in any higher-dimensional polytopes in the database.
| Notable Tetrashapes | |
| Regular: | pyrochoron • aerochoron • geochoron • xylochoron • hydrochoron • cosmochoron |
| Powertopes: | triangular octagoltriate • square octagoltriate • hexagonal octagoltriate • octagonal octagoltriate |
| Circular: | glome • cubinder • duocylinder • spherinder • sphone • cylindrone • dicone • coninder |
| Torii: | tiger • torisphere • spheritorus • torinder • ditorus |