Spherinder (EntityTopic, 14)
From Hi.gher. Space
A spherinder is a special case of the prism where the base is a sphere. It is bounded by two spheres and a 3-manifold formed by the extrusion of a sphere in 4-space.
Equations
- Variables:
r ⇒ radius of the spherinder
h ⇒ height of the spherinder
- All points (x, y, z, w) that lie on the surcell of a spherinder will satisfy the following equation:
Unknown
- The hypervolumes of a spherinder are given by:
total edge length = 0
total surface area = 8π · r2
surcell volume = 8π∕3 · r3 + 4π · r2h
bulk = 4π∕3 · r3h
- The realmic cross-sections (n) of a spherinder are:
[!x,!y,!z] ⇒ cylinder with radius (2rcos(πn/2)), height (h)
[!w] ⇒ sphere of radius (r)
Cross-sections
Round cell-first:Ball-first:
Face-first:
Projection
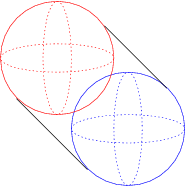
The spherical cylinder, or spherinder for short, is constructed by extruding a 3D sphere along the W-axis for a unit distance. The resulting shape is the best 4D analog of the 3D cylinder, having two spherical “lids” connected by an extended spherical volume. The following diagram shows a parallel projection of a spherinder.
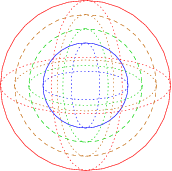
Unfortunately, because of the smoothness of the 3D spheres, a wire-diagram such as this one doesn't adequately show the internal structure of the spherinder. The following perspective projection diagram tries to better capture the structure of the center section of the spherinder:
This diagram requires explanation. The outer red sphere is the near end of the spherinder, and the inner blue sphere is the far end. The two intermediate spheres are cross sections of the 3D surface that connects these two ends. Although they appear as concentric spheres in the projection, they are actually disjoint spheres of the same size, displaced at different distances along the W-axis. One can imagine this diagram as being analogous to looking through one end of a 3D cylinder and seeing the circular lid at the other end. The cross sections of the circular tubing in between would appear as concentric circles of different sizes.
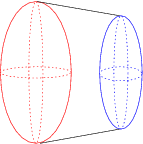
The next diagram shows the spherinder at an angle in a perspective projection, with its far end rotated part way toward the horizontal X-axis.
Here, we see that the red spherical end of the spherinder has been partially flattened into an ellipsoid. The blue end has “emerged” outside the red end, and has also been partly flattened into an ellipsoid. The uneven sizes indicate that the long axis of the spherinder is still partly rotated into the W-axis. Of course, the spherical ends of the spherinder aren't actually being flattened; they only appear that way because they are being viewed at from an angle.
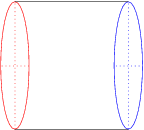
The last diagram below shows the spherinder rotated so that its long axis fully coincides with the X-axis.
As the reader can see, the dotted equitorial curves of the two spherical ends have flattened into intersecting straight lines. The two spherical ends have completely flattened into circles. Thus this projection of the spherinder is a 3D cylinder. Of course, in actuality the two ends are still as spherical as before; they appear as circles because they are being viewed at from a 90-degree angle.
The spherinder can cover a 2D area by rolling because every section perpendicular to its long axis is a 3D sphere. These constituent spheres can roll synchronously in two perpendicular directions.
| Notable Tetrashapes | |
| Regular: | pyrochoron • aerochoron • geochoron • xylochoron • hydrochoron • cosmochoron |
| Powertopes: | triangular octagoltriate • square octagoltriate • hexagonal octagoltriate • octagonal octagoltriate |
| Circular: | glome • cubinder • duocylinder • spherinder • sphone • cylindrone • dicone • coninder |
| Torii: | tiger • torisphere • spheritorus • torinder • ditorus |
| 12. 4 Glome | 13. 31 Spherinder | 14. 22 Duocylinder |
| List of tapertopes | ||
| 6a. (II)(II) Duocylinder | 6b. ((II)(II)) Tiger | 7a. (III)I Spherinder | 7b. ((III)I) Torisphere | 8a. ((II)I)I Torinder | 8b. (((II)I)I) Ditorus |
| List of toratopes | |||||
| 16. [<III>I] Octahedral prism | 17. [(III)I] Spherinder | 18. <[III]I> Cubic bipyramid |
| List of bracketopes | ||