Cubinder (EntityTopic, 14)
From Hi.gher. Space
m |
Icebreaker (Talk | contribs) |
||
| (15 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| + | <[#ontology [kind topic] [cats 4D Curved Rotatope]]> | ||
{{STS Shape | {{STS Shape | ||
| name=Cubinder | | name=Cubinder | ||
| dim=4 | | dim=4 | ||
| - | | elements= | + | | elements=4 [[cylinder]]s, 1 square hose, 4 [[circle]]s, 4 hoses, 4 circular edges, 0 |
| genus=0 | | genus=0 | ||
| ssc=[(xy)zw] | | ssc=[(xy)zw] | ||
| ssc2=++T2 | | ssc2=++T2 | ||
| - | | extra={{STS | + | | pv_square=<sup>π</sup>⁄<sub>4</sub> ≈ 0.7854 |
| - | | | + | | extra={{STS Tapertope |
| - | | notation=211 ( | + | | order=3, 0 |
| - | | index= | + | | notation=211 |
| + | | index=15 | ||
| + | }}{{STS Toratope | ||
| + | | expand=[[Cubinder|211]] | ||
| + | | notation=(II)II | ||
| + | | index=5a | ||
}}{{STS Bracketope | }}{{STS Bracketope | ||
| - | | index= | + | | index=13 |
| - | }}}} | + | | notation=[(II)II]}}}} |
| - | A '''cubinder''' is a special case of | + | A '''cubinder''' is a special case of a [[prism]] where the base is a [[cylinder]]. It is also the limiting shape of an n,4-[[duoprism]] as n approaches infinity. In other words, it is the [[Cartesian product]] of a [[circle]] and a [[square]]. |
== Equations == | == Equations == | ||
*Variables: | *Variables: | ||
<blockquote>''r'' ⇒ radius of the cubinder<br> | <blockquote>''r'' ⇒ radius of the cubinder<br> | ||
| - | '' | + | ''h'' ⇒ height of the cubinder along z and w axes</blockquote> |
| - | + | ||
*All points (''x'', ''y'', ''z'', ''w'') that lie on the [[surcell]] of a cubinder will satisfy the following equations: | *All points (''x'', ''y'', ''z'', ''w'') that lie on the [[surcell]] of a cubinder will satisfy the following equations: | ||
<blockquote>''x''<sup>2</sup> + ''y''<sup>2</sup> = ''r''<sup>2</sup> <br> | <blockquote>''x''<sup>2</sup> + ''y''<sup>2</sup> = ''r''<sup>2</sup> <br> | ||
| - | abs(''z'') ≤ '' | + | abs(''z'') ≤ ''h'' <br> |
| - | abs(''w'') ≤ '' | + | abs(''w'') ≤ ''h'' <br> |
-- or --<br> | -- or --<br> | ||
''x''<sup>2</sup> + ''y''<sup>2</sup> < ''r''<sup>2</sup> <br> | ''x''<sup>2</sup> + ''y''<sup>2</sup> < ''r''<sup>2</sup> <br> | ||
| - | abs(''z'') = '' | + | abs(''z'') = ''h'' <br> |
| - | abs(''w'') = '' | + | abs(''w'') = ''h'' <br> |
</blockquote> | </blockquote> | ||
*The [[hypervolume]]s of a cubinder are given by: | *The [[hypervolume]]s of a cubinder are given by: | ||
<blockquote>total edge length = 8π''r''<br> | <blockquote>total edge length = 8π''r''<br> | ||
| - | total surface area = 4π''r''(''r'' + '' | + | total surface area = 4π''r''(''r'' + 2''h'')<br> |
| - | surcell volume = 2π''r''('' | + | surcell volume = 2π''r''(''rh'' + ''h''<sup>2</sup>)<br> |
| - | bulk = π''r''<sup>2</sup>'' | + | bulk = π''r''<sup>2</sup>''h''<sup>2</sup></blockquote> |
*The [[realmic]] [[cross-section]]s (''n'') of a cubinder are: | *The [[realmic]] [[cross-section]]s (''n'') of a cubinder are: | ||
| - | <blockquote> | + | <blockquote>[!x,!y] ⇒ square cuboid<br> |
| + | [!z,!w] ⇒ cylinder | ||
| + | </blockquote> | ||
== Net == | == Net == | ||
| - | The net of a cubinder is a | + | The net of a cubinder is a square prism surrounded by four cylinders: |
| + | |||
| + | <blockquote><[#embed [hash 6XMAYS6F8E9MYP67GCF9YR0D79]]></blockquote> | ||
| + | |||
| + | == Cross-sections == | ||
| + | |||
| + | Round cell-first: | ||
| + | |||
| + | <[#embed [hash YZ41PJNVNNC6ACHMN7STTY61QZ]]> | ||
| + | |||
| + | Cylinder-first: | ||
| + | |||
| + | <[#embed [hash N15NMRF09MKWWPQWR9V1W4XHD4]]> | ||
| + | |||
| + | Disk-first: | ||
| + | |||
| + | <[#embed [hash 88YAG700KXXBGCSTG7Y7RHK54Z]]> | ||
| + | |||
| + | Round face-first: | ||
| + | |||
| + | <[#embed [hash A3SVTKKX03GYTKSFZTDCCZSV9G]]> | ||
| + | |||
| + | Edge-first: | ||
| + | |||
| + | <[#embed [hash SDQXJNECFXCGWFCWTHH089353M]]> | ||
| - | |||
== Projection == | == Projection == | ||
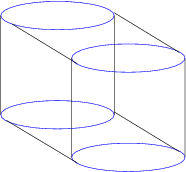
The cubical cylinder, or cubinder for short, is one of the ways to generalize the 3D cylinder to 4D. This object can be constructed by extruding a 3D cylinder along the W-axis by a unit distance. The following is a diagram of the cubinder in parallel projection: | The cubical cylinder, or cubinder for short, is one of the ways to generalize the 3D cylinder to 4D. This object can be constructed by extruding a 3D cylinder along the W-axis by a unit distance. The following is a diagram of the cubinder in parallel projection: | ||
| - | <blockquote> | + | <blockquote><[#embed [hash HPFYM7SBJ9FXM8ZQKM5ZYFB0CF]]></blockquote> |
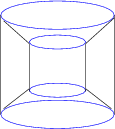
The following is a perspective projection of the cubinder: | The following is a perspective projection of the cubinder: | ||
| - | <blockquote> | + | <blockquote><[#embed [hash S9ZZWC7D8T80TW4DZ13GMAZVT9]]></blockquote> |
The inner cylinder is actually the same size as the outer cylinder, but appears smaller in perspective because it is farther away. Also, the upper and lower frustums connecting the inner cylinder to the outer cylinder are actually themselves regular cylinders; but they appear as frustums because they are being viewed at from an angle. | The inner cylinder is actually the same size as the outer cylinder, but appears smaller in perspective because it is farther away. Also, the upper and lower frustums connecting the inner cylinder to the outer cylinder are actually themselves regular cylinders; but they appear as frustums because they are being viewed at from an angle. | ||
| Line 59: | Line 89: | ||
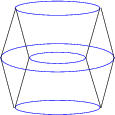
And the next diagram shows another perspective projection, this time with the cubinder rotated 45 degrees in the ZW plane. | And the next diagram shows another perspective projection, this time with the cubinder rotated 45 degrees in the ZW plane. | ||
| - | <blockquote> | + | <blockquote><[#embed [hash 27T4WXZCVFKM04SGXWJVPHHE1G]]></blockquote> |
Here, it is more apparent that the cubinder consists of four 3D cylinders joined at their circular ends. What is not so apparent, however, is that their round surfaces are joined by a square torus. This is the torus generated by rotating a square in the ZW plane (displaced in the Y direction by one unit) in the XY plane. One could also construct it by extruding the round part of the cylinder along the W-axis. | Here, it is more apparent that the cubinder consists of four 3D cylinders joined at their circular ends. What is not so apparent, however, is that their round surfaces are joined by a square torus. This is the torus generated by rotating a square in the ZW plane (displaced in the Y direction by one unit) in the XY plane. One could also construct it by extruding the round part of the cylinder along the W-axis. | ||
| Line 67: | Line 97: | ||
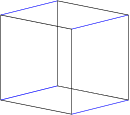
The reason for the cubinder's name is that one of its possible projections is the 3D cube: | The reason for the cubinder's name is that one of its possible projections is the 3D cube: | ||
| - | <blockquote> | + | <blockquote><[#embed [hash VH41MBR55AER66PBXH35GPNMMM]]></blockquote> |
The blue edges in the cube show where the 4 circular ends of the cylinders are. They have collapsed into a single line in the diagram because they are perpendicular to the direction of projection. | The blue edges in the cube show where the 4 circular ends of the cylinders are. They have collapsed into a single line in the diagram because they are perpendicular to the direction of projection. | ||
== Rolling == | == Rolling == | ||
| - | |||
There are 4 circular surfaces on the cubinder, on which it may roll. All 4 surfaces, however, can only rotate parallel to the same plane, and hence the cubinder can only cover the space of a line by rolling. (This may sound counterintuitive to our 3D-centered understanding of rotation, because the 4 cylinders are in 2 perpendicular pairs, and so have perpendicular central axes. In 3D, two perpendicular central axis define two different planes of rotation. However, in 4D, rotations don't happen around an axis, but around a plane. The perpendicular central axes of the cubinder are actually both perpendicular to the plane of rotation. As one can see from the diagrams above, all circular sections of the cubinder lie parallel to the same plane, and hence can only rotate in that plane.) | There are 4 circular surfaces on the cubinder, on which it may roll. All 4 surfaces, however, can only rotate parallel to the same plane, and hence the cubinder can only cover the space of a line by rolling. (This may sound counterintuitive to our 3D-centered understanding of rotation, because the 4 cylinders are in 2 perpendicular pairs, and so have perpendicular central axes. In 3D, two perpendicular central axis define two different planes of rotation. However, in 4D, rotations don't happen around an axis, but around a plane. The perpendicular central axes of the cubinder are actually both perpendicular to the plane of rotation. As one can see from the diagrams above, all circular sections of the cubinder lie parallel to the same plane, and hence can only rotate in that plane.) | ||
{{Tetrashapes}} | {{Tetrashapes}} | ||
| - | {{ | + | {{Tapertope Nav|14|15|16|22<br>Duocylinder|211<br>Cubinder|1111<br>Tesseract|chora}} |
| - | {{Bracketope Nav| | + | {{Toratope Nav A|4|5|6|IIII<br>Tesseract|(IIII)<br>Glome|(II)II<br>Cubinder|((II)II)<br>Spheritorus|(II)(II)<br>Duocylinder|((II)(II))<br>Tiger|chora}} |
| - | + | {{Bracketope Nav|12|13|14|(IIII)<br>Glome|[(II)II]<br>Cubinder|<(II)II><br>Dibicone|chora}} | |
| - | + | ||
Latest revision as of 10:12, 19 June 2018
A cubinder is a special case of a prism where the base is a cylinder. It is also the limiting shape of an n,4-duoprism as n approaches infinity. In other words, it is the Cartesian product of a circle and a square.
Equations
- Variables:
r ⇒ radius of the cubinder
h ⇒ height of the cubinder along z and w axes
- All points (x, y, z, w) that lie on the surcell of a cubinder will satisfy the following equations:
x2 + y2 = r2
abs(z) ≤ h
abs(w) ≤ h
-- or --
x2 + y2 < r2
abs(z) = h
abs(w) = h
- The hypervolumes of a cubinder are given by:
total edge length = 8πr
total surface area = 4πr(r + 2h)
surcell volume = 2πr(rh + h2)
bulk = πr2h2
- The realmic cross-sections (n) of a cubinder are:
[!x,!y] ⇒ square cuboid
[!z,!w] ⇒ cylinder
Net
The net of a cubinder is a square prism surrounded by four cylinders:
Cross-sections
Round cell-first:
Cylinder-first:
Disk-first:
Round face-first:
Edge-first:
Projection
The cubical cylinder, or cubinder for short, is one of the ways to generalize the 3D cylinder to 4D. This object can be constructed by extruding a 3D cylinder along the W-axis by a unit distance. The following is a diagram of the cubinder in parallel projection:
The following is a perspective projection of the cubinder:
The inner cylinder is actually the same size as the outer cylinder, but appears smaller in perspective because it is farther away. Also, the upper and lower frustums connecting the inner cylinder to the outer cylinder are actually themselves regular cylinders; but they appear as frustums because they are being viewed at from an angle.
And the next diagram shows another perspective projection, this time with the cubinder rotated 45 degrees in the ZW plane.
Here, it is more apparent that the cubinder consists of four 3D cylinders joined at their circular ends. What is not so apparent, however, is that their round surfaces are joined by a square torus. This is the torus generated by rotating a square in the ZW plane (displaced in the Y direction by one unit) in the XY plane. One could also construct it by extruding the round part of the cylinder along the W-axis.
These diagrams do not have hidden surfaces removed, so that the whole structure of the cubinder is more apparent. However, a 4D being looking at the cubinder would not see the entire structure simultaneously. The inner cylinder in the second diagram would not be visible, for example, and neither would the two inner cylinders in the second diagram.
The reason for the cubinder's name is that one of its possible projections is the 3D cube:
The blue edges in the cube show where the 4 circular ends of the cylinders are. They have collapsed into a single line in the diagram because they are perpendicular to the direction of projection.
Rolling
There are 4 circular surfaces on the cubinder, on which it may roll. All 4 surfaces, however, can only rotate parallel to the same plane, and hence the cubinder can only cover the space of a line by rolling. (This may sound counterintuitive to our 3D-centered understanding of rotation, because the 4 cylinders are in 2 perpendicular pairs, and so have perpendicular central axes. In 3D, two perpendicular central axis define two different planes of rotation. However, in 4D, rotations don't happen around an axis, but around a plane. The perpendicular central axes of the cubinder are actually both perpendicular to the plane of rotation. As one can see from the diagrams above, all circular sections of the cubinder lie parallel to the same plane, and hence can only rotate in that plane.)
| Notable Tetrashapes | |
| Regular: | pyrochoron • aerochoron • geochoron • xylochoron • hydrochoron • cosmochoron |
| Powertopes: | triangular octagoltriate • square octagoltriate • hexagonal octagoltriate • octagonal octagoltriate |
| Circular: | glome • cubinder • duocylinder • spherinder • sphone • cylindrone • dicone • coninder |
| Torii: | tiger • torisphere • spheritorus • torinder • ditorus |
| 14. 22 Duocylinder | 15. 211 Cubinder | 16. 1111 Tesseract |
| List of tapertopes | ||
| 4a. IIII Tesseract | 4b. (IIII) Glome | 5a. (II)II Cubinder | 5b. ((II)II) Spheritorus | 6a. (II)(II) Duocylinder | 6b. ((II)(II)) Tiger |
| List of toratopes | |||||
| 12. (IIII) Glome | 13. [(II)II] Cubinder | 14. <(II)II> Dibicone |
| List of bracketopes | ||