Glome (EntityTopic, 15)
From Hi.gher. Space
The glome, also known as the 3-sphere, is the 4-dimensional equivalent of a 3D sphere. It consists of a curved 3-manifold that forms circular intersections with planes, and spherical intersections with hyperplanes. The set of points midway between two antipodal points form a sphere, hence one may think of the glome as having a spherical "equator". Alternatively, one can think of the glome having two perpendicular circular equators - and no poles!
Sometimes, the word glome refers to the surface, while the solid 4-D object is called a gongol.
Its projection to 3-space is a sphere — or, more properly, a ball: the image of its bounding manifold covers all points in a ball twice, once for each hemi-glome.
Equations
- Variables:
r ⇒ radius of the glome
- All points (x, y, z, w) that lie on the surcell of a glome will satisfy the following equation:
x2 + y2 + z2 + w2 = r2
- The hypervolumes of a glome are given by:
total edge length = 0
total surface area = 0
surcell volume = 2π2 · r3
bulk = π2∕2 · r4
- The realmic cross-sections (n) of a glome are:
[!x,!y,!z,!w] ⇒ sphere of radius (rcos(πn/2))
Visualization
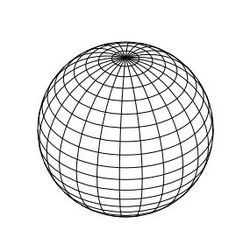
We can visualize the glome by looking at subdivisions of it. First, we'll show a subdivision of the sphere:
The first diagram above shows a wireframe subdivision; the second shows this subdivision projected into 2D with hidden surface removal performed.
There are two main subdivisions of the glome. The first is analogous to the second image above:
Here we can see the "pole" of the glome, the point in the middle near the top where all the curves converge, similar to the pole in the sphere diagram. In the sphere diagram, we have two types of curves: those of latitude, which are the circles that surround the pole without touching it, and those of longitude, which are the circles which go through the pole and come out the other side. In the glome subdivision, the curves of latitude become spheres surrounding the pole, getting bigger and bigger until they reach the projection envelope. The curves of longitude stay as one-dimensional curves, but spread out in two dimensions instead of one: they connect the pole to all points on the "spheres of latitude".
The second subdivision arranges the rind of the glome like that of a duocylinder:
In this subdivision, the two highlighted regions (yellow and magenta) are toruses. These toruses are actually analogous to the lines of latitude in the sphere subdivision. If you look hard enough, you can actually see one more torus between the yellow and purple ones, which has been squashed so much by the projection it looks more like a cylinder. This unmarked torus is actually the "toric equator", or toroquator. Similarly, there is a line running vertically down the center of the yellow torus, which is really a circle, and there is another circle just outside the projection envelope (thus invisible) but which would be almost in the center of the magenta torus. These two circles are actually the "poles", or toropoles of the glome - let's say the one in the yellow torus is the north toropole, and the other one, in the magenta torus, is the south toropole. The rind of the glome is traced out as the sweep of a torus moving from the north toropole, through the yellow torus, through the toroquator, through the magenta torus to the south toropole. At each toropole, the radius would be zero, thus degenerating into a circle, much like how a circle tracing out the surface of a sphere degenerates into a point at each pole.
| Notable Tetrashapes | |
| Regular: | pyrochoron • aerochoron • geochoron • xylochoron • hydrochoron • cosmochoron |
| Powertopes: | triangular octagoltriate • square octagoltriate • hexagonal octagoltriate • octagonal octagoltriate |
| Circular: | glome • cubinder • duocylinder • spherinder • sphone • cylindrone • dicone • coninder |
| Torii: | tiger • torisphere • spheritorus • torinder • ditorus |
| 11. 12 Tetrahedron | 12. 4 Glome | 13. 31 Spherinder |
| List of tapertopes | ||
| 3a. (II)I Cylinder | 3b. ((II)I) Torus | 4a. IIII Tesseract | 4b. (IIII) Glome | 5a. (II)II Cubinder | 5b. ((II)II) Spheritorus |
| List of toratopes | |||||
| 11. <IIII> Aerochoron | 12. (IIII) Glome | 13. [(II)II] Cubinder |
| List of bracketopes | ||