Conway symbol (InstanceTopic, 3)
From Hi.gher. Space
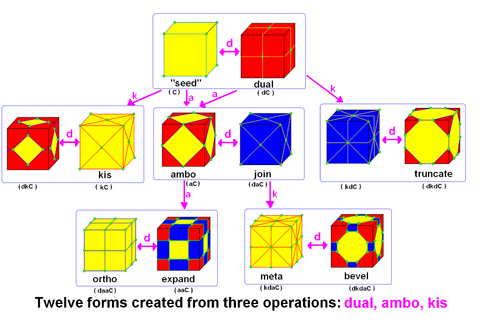
Conway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operators.
The seed polyhedra are the Platonic solids, represented by their first letter of their name (T, O, C, I, D); the prisms (Pn), antiprisms (An) and pyramids (Yn). Any convex polyhedron can serve as a seed, as long as the operations can be executed on it.
John Conway extended the idea of using operators, like truncation defined by Kepler, to build related polyhedra of the same symmetry. His descriptive operators that can generate all the Archimedean solids and Catalan solids from regular seeds. Applied in a series, these operators allows many higher order polyhedra to be generated.
Since all seed polyhedra can be made from Y3, the symbols T, O, C, I and D will not be used in STS templates. The compound symbols j, k, o, b, m, g will also not be used.
Operations on polyhedra
| Operator | Name | Alternate construction | vertices | edges | faces | Description |
|---|---|---|---|---|---|---|
| seed | v | e | f | seed form | ||
| d | dual | f | e | v | dual of the seed polyhedron - each vertex creates a new face | |
| a | ambo | e | 2e | 2+e | truncates to the edge midpoints, each vertex creates a new face. (rectification) | |
| j | join | da | e+2 | 2e | e | new kite-shaped faces are created in place of each edge. |
| t | truncate | 2e | 3e | e+2 | truncate all vertices. | |
| -- | -- | dt | e+2 | 3e | 2e | dual of truncation (bitruncation) |
| -- | -- | dk | 2e | 3e | e+2 | dual of kis |
| k | kis | dtd | e+2 | 3e | 2e | raises a pyramid on each face. |
| e | expand | 2e | 4e | 2e+2 | Each vertex creates a new face and each edge creates a new quadrilateral. (cantellation) | |
| o | ortho | de | 2e+2 | 4e | 2e | Each n-gon faces are divided into n quadrilaterals. |
| b | bevel | ta | 4e | 5e | 2e+2 | New faces are added in place of edges and vertices. |
| m | meta | db & kj | 2e+2 | 5e | 4e | n-gon faces are divided into 2n triangles |
| s | snub | 2e | 5e | 3e+2 | "expand and twist" - each vertex creates a new face and each edge creates two new triangles | |
| g | gyro | ds | 3e+2 | 5e | 2e | Each n-gon face is divided into n pentagons. |
Special forms
- The kis operator has a variation, kn, which only adds pyramids to n-sided faces.
- The truncate operator has a variation, tn, which only truncates order-n vertices.
The operators are applied like functions from right to left. For example:
- the dual of a tetrahedron is dT;
- the truncation of a cube is t3C or tC;
- the truncation of a cuboctahedron is t4aC or taC.
All operations are symmetry-preserving except twisting ones like s and g which lose reflection symmetry.
Examples
The cube can generate all the convex Octahedral symmetry uniform polyhedra. The first row generates the Archimedean solids and the second row the Catalan solids, the second row forms being duals of the first. Comparing each new polyhedron with the cube, each operation can be visually understood. (Two polyhedron forms don't have single operator names given by Conway.)
| Cube "seed" | ambo (Rectification) | truncate | bitruncate | expand (cantellation) | bevel (omnitruncation) | snub |
|---|---|---|---|---|---|---|
 C |  aC = djC |  tC = dkdC |  tdC = dkC |  eC = aaC = doC | 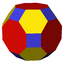 bC = taC = dmC = dkjC |  sC = dgC |
| dual | join | kis (vertex-bisect) | ortho (edge-bisect) | meta (full-bisect) | gyro | |
 dC | 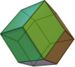 jC = daC | 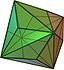 kdC = dtC |  kC = dtdC | 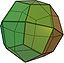 oC = deC | 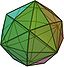 mC = dbC = kjC |  gC = dsC |
Generating regular seeds
All of the five regular polyhedra can be generated from the tetrahedron, Y3, with zero to two operators:
- T = Y3
- O = aY3 (Rectified tetrahedron)
- C = daY3 (dual to rectified tetrahedron)
- I = sY3 (snub tetrahedron)
- D = dsY3 (dual to snub tetrahedron)
Extensions to Conway's symbols
The above operations allow all of the semiregular polyhedrons and Catalan solids to be generated from regular polyhedrons. Combined many higher operations can be made, but many interesting higher order polyhedra require new operators to be constructed.
For example, geometric artist George W. Hart [1] create an operation he called a propellor, and another reflect to create mirror images of the rotated forms.
- p - "propellor" (A rotation operator that creates quadrilaterals at the vertices). This operation is self-dual: dpX=pdX.
- r - "reflect" - makes the mirror image of the seed; it has no effect unless the seed was made with s or p.
Geometric coordinates of derived forms
In general the seed polyhedron can be considered a tiling of a surface since the operators represent topological operations so the exact geometric positions of the vertices of the derived forms are not defined in general. A convex regular polyhedron seed can be considered a tiling on a sphere, and so the derived polyhedron can equally be assumed to be positioned on the surface of a sphere. Similar a regular tiling on a plane, such as a hexagonal tiling can be a seed tiling for derived tilings. Nonconvex polyhedra can become seeds if a related topological surface is defined to constrain the positions of the vertices. For example torus-shaped polyhedra can derived other polyhedra with point on the same torus surface.
 D | 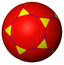 tD |  aD |  tdD |  dD |  eD |  teD |