Cosmochoron (EntityTopic, 12)
From Hi.gher. Space
(Add description, add section on relation to grand antiprism) |
Username5243 (Talk | contribs) (→Coordinates) |
||
| (19 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| + | <[#ontology [kind topic] [cats 4D Regular Polytope]]> | ||
{{STS Shape | {{STS Shape | ||
| dim=4 | | dim=4 | ||
| - | | elements=120, 720, 1200, 600 | + | | elements=120 [[Dodecahedron|dodecahedra]], 720 [[pentagon]]s, 1200 [[digon]]s, 600 [[point]]s |
| genus=0 | | genus=0 | ||
| ssc=<nowiki>{{</nowiki>G5<sup>3</sup>}<sup>4</sup>} | | ssc=<nowiki>{{</nowiki>G5<sup>3</sup>}<sup>4</sup>} | ||
| - | | extra={{STS Uniform polytope | + | | ssc2=Ks1 |
| + | | extra={{STS Polytope | ||
| + | | flayout={{FLD|dim=4|left=e3|erev|a5|end2|e3}} | ||
| + | | petrie=30, 60, 30, 60,<br>60, 60, 60, 60,<br>60, 30, 60, 30, 0 | ||
| + | | dual=[[Hydrochoron]] | ||
| + | | bowers=Hi | ||
| + | }}{{STS Uniform polytope | ||
| schlaefli={[[Pentagon|5,]][[Dodecahedron|3,]]3} | | schlaefli={[[Pentagon|5,]][[Dodecahedron|3,]]3} | ||
| + | | dynkin=x5o3o3o | ||
| vlayout=([[Pentagon|5]][[Dodecahedron|<sup>3</sup>]])<sup>4</sup> | | vlayout=([[Pentagon|5]][[Dodecahedron|<sup>3</sup>]])<sup>4</sup> | ||
| - | | vfigure=[[ | + | | vfigure=[[Tetrahedron]] |
| - | + | ||
| - | + | ||
| - | + | ||
}}}} | }}}} | ||
| - | The ''' | + | The '''cosmochoron''', also known as the '''hecatonicosachoron''' and the '''120-cell''', is a 4D polytope bounded by 120 [[dodecahedra]]. It is the highest dimensional analog of the [[pentagon]] and the dodecahedron. |
| - | + | Each dodecahedron in its [[net]] lies on a ring of ten dodecahedra along a [[great circle]] of the [[glome]]. There are four dodecahedra on such a ring between any dodecahedron and its antipodal dodecahedron. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ==Coordinates== | |
| - | < | + | The coordinates of the 120-cell with edge length 2/φ<sup>2</sup> are all permutations of coordinates and changes of sign of: |
| - | + | (2, 2, 0, 0)<br> | |
| - | + | (√5, 1, 1, 1)<br> | |
| - | + | (φ, φ, φ, 2-φ)<br> | |
| - | + | (φ+1, φ−1, φ−1, φ−1)<br> | |
| - | + | ||
| - | + | Together with all even permutations of coordinates and all changes of sign of: | |
| - | + | ||
| - | + | (φ+1, 2-φ, 1, 0)<br> | |
| - | + | (√5, φ−1, φ, 0)<br> | |
| + | (2, 1, φ, φ−1)<br> | ||
| - | + | == Equations == | |
| + | *The [[hypervolume]]s of a cosmochoron with side length ''l'' are given by: | ||
| + | <blockquote>total edge length = 1200''l''<br> | ||
| + | total surface area = 180√(25 + 10√5) {{DotHV}}<br> | ||
| + | surcell volume = 30(15 + 7√5) {{DotHV|3}}<br> | ||
| + | bulk = {{Over|15|4}}(105 + 47√5) {{DotHV|4}}</blockquote> | ||
| - | == | + | == Projection == |
| + | <[#embed [hash XN0PP2G3K4HZT6489B2ZYT8D15]]> <[#embed [hash NK06P7XH2G01YTY3EYK0T5BGDQ]]> | ||
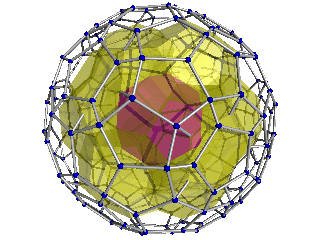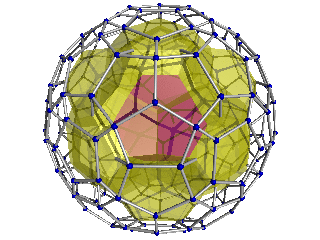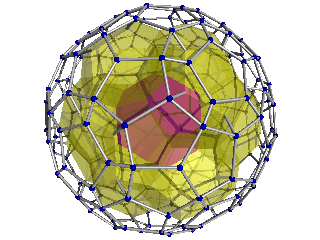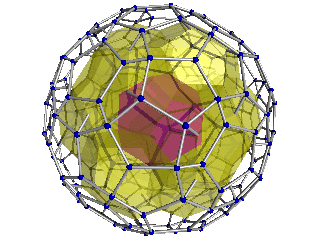
| - | + | Here are two perspective projections of the hecatonicosachoron into 3D. The highlighted center cell is closest to the 4D viewpoint. It is surrounded by 12 [[dodecahedra]] in a second layer. The right-hand image also shows the third layer of 32 dodecahedra. After this is a fourth layer of 30 dodecahedra lying on the spherical "equator", followed by three more layers mirroring the three layers seen here (not seen here, because they lie on the 4D "back" of the shape). | |
| - | + | Note that only the projection is rotating; the 4D shape itself is not. | |
| - | + | <[#polytope [id 40]]> | |
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
{{Tetrashapes}} | {{Tetrashapes}} | ||
| - | |||
| - | |||
Latest revision as of 15:34, 26 March 2017
The cosmochoron, also known as the hecatonicosachoron and the 120-cell, is a 4D polytope bounded by 120 dodecahedra. It is the highest dimensional analog of the pentagon and the dodecahedron.
Each dodecahedron in its net lies on a ring of ten dodecahedra along a great circle of the glome. There are four dodecahedra on such a ring between any dodecahedron and its antipodal dodecahedron.
Coordinates
The coordinates of the 120-cell with edge length 2/φ2 are all permutations of coordinates and changes of sign of:
(2, 2, 0, 0)
(√5, 1, 1, 1)
(φ, φ, φ, 2-φ)
(φ+1, φ−1, φ−1, φ−1)
Together with all even permutations of coordinates and all changes of sign of:
(φ+1, 2-φ, 1, 0)
(√5, φ−1, φ, 0)
(2, 1, φ, φ−1)
Equations
- The hypervolumes of a cosmochoron with side length l are given by:
total edge length = 1200l
total surface area = 180√(25 + 10√5) · l2
surcell volume = 30(15 + 7√5) · l3
bulk = 15∕4(105 + 47√5) · l4
Projection
Here are two perspective projections of the hecatonicosachoron into 3D. The highlighted center cell is closest to the 4D viewpoint. It is surrounded by 12 dodecahedra in a second layer. The right-hand image also shows the third layer of 32 dodecahedra. After this is a fourth layer of 30 dodecahedra lying on the spherical "equator", followed by three more layers mirroring the three layers seen here (not seen here, because they lie on the 4D "back" of the shape).
Note that only the projection is rotating; the 4D shape itself is not.
Incidence matrix
Dual: hydrochoron
| # | TXID | Va | Ea | 5a | C1a | Type | Name |
|---|---|---|---|---|---|---|---|
| 0 | Va | = point | ; | ||||
| 1 | Ea | 2 | = digon | ; | |||
| 2 | 5a | 5 | 5 | = pentagon | ; | ||
| 3 | C1a | 20 | 30 | 12 | = dodecahedron | ; | |
| 4 | H4.1a | 600 | 1200 | 720 | 120 | = cosmochoron | ; |
Usage as facets
This polytope does not currently appear as facets in any higher-dimensional polytopes in the database.
| Notable Tetrashapes | |
| Regular: | pyrochoron • aerochoron • geochoron • xylochoron • hydrochoron • cosmochoron |
| Powertopes: | triangular octagoltriate • square octagoltriate • hexagonal octagoltriate • octagonal octagoltriate |
| Circular: | glome • cubinder • duocylinder • spherinder • sphone • cylindrone • dicone • coninder |
| Torii: | tiger • torisphere • spheritorus • torinder • ditorus |