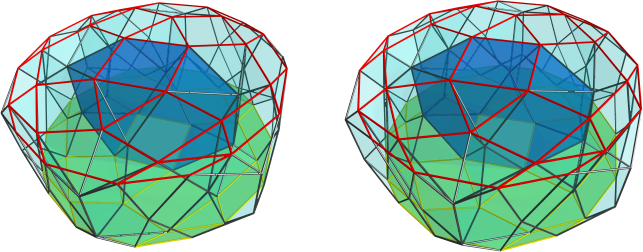Castellated rhodoperihedral prism (EntityTopic, 15)
From Hi.gher. Space
The castellated rhodoperihedral prism is a bilbirothawroid discovered on February 4, 2014 by quickfur and confirmed by Klitzing.[1] Although it is not strictly a prism (as it's not the Cartesian product of a base shape with a digon) it is so named as it has similar structure to "real" prisms of uniform polyhedra.
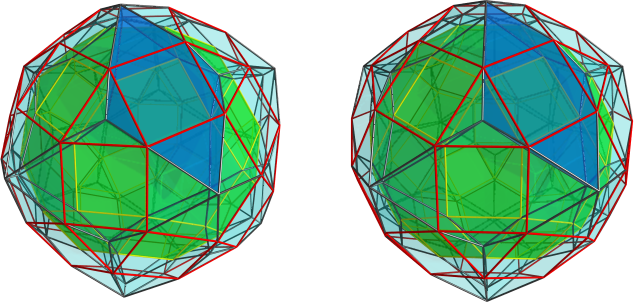
Its cells are two rhodoperihedra, 24 pentagonal pyramids, 40 tetrahedra and 30 bilunabirotundae (bilbiro). The rhodoperihedra form the "ends" of the prism, and are orthogonal to the bilbiro, which form the "sides" of the prism.
Its faces are 40 "end" triangles (x3o), 60 "end" squares (x2x), 24 "end" pentagons (o5x), 120 "lune-facing side" triangles (xo&#x), 120 "rotunda-facing side" triangles (xo&#x) and 60 "side" pentagons (ooooo3ooooo5ooooo&#xt).
It has 120 + 120 + 120 + 120 + 12 = 492 edges and 120 + 24 + 20 = 164 vertices.
Equations
- The hypervolumes of a castellated rhodoperihedral prism with side length l are given by:
total edge length = 492l
total surface area = (60 + 70√3 + 21√(25+10√5)) · l2
surcell volume = 1∕3 · (60φ2 + 197φ + 74 + 10√2) · l3
bulk = Unknown
Projections
Centered on a rhodoperihedron:
Centered on a bilunabirotunda (J91):
Coordinates
The Cartesian coordinates of the castellated rhodoperihedral prism are:
| Top and bottom x5o3x | Two φ2-scaled icosahedra | φ-scaled dodecahedron |
|---|---|---|
|
|
|
where φ=(1+√5)/2 is the Golden Ratio.
Incidence matrix
Dual: D4.3.1 dual
| # | TXID | Va | Vb | Vc | Ea | Eb | Ec | Ed | Ee | 3a | 4a | 5a | 3b | 3c | 5b | C1a | C2a | C3a | C4a | Type | Name |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Va | = point | ; | ||||||||||||||||||
| 1 | Vb | = point | ; | ||||||||||||||||||
| 2 | Vc | = point | ; | ||||||||||||||||||
| 3 | Ea | 2 | 0 | 0 | = digon | ; | |||||||||||||||
| 4 | Eb | 2 | 0 | 0 | = digon | ; | |||||||||||||||
| 5 | Ec | 1 | 1 | 0 | = digon | ; | |||||||||||||||
| 6 | Ed | 1 | 0 | 1 | = digon | ; | |||||||||||||||
| 7 | Ee | 0 | 2 | 0 | = digon | ; | |||||||||||||||
| 8 | 3a | 3 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | = triangle | ; | ||||||||||
| 9 | 4a | 4 | 0 | 0 | 2 | 2 | 0 | 0 | 0 | = square | ; | ||||||||||
| 10 | 5a | 5 | 0 | 0 | 0 | 5 | 0 | 0 | 0 | = pentagon | ; | ||||||||||
| 11 | 3b | 2 | 1 | 0 | 0 | 1 | 2 | 0 | 0 | = triangle | ; | ||||||||||
| 12 | 3c | 2 | 0 | 1 | 1 | 0 | 0 | 2 | 0 | = triangle | ; | ||||||||||
| 13 | 5b | 2 | 2 | 1 | 0 | 0 | 2 | 2 | 1 | = pentagon | ; | ||||||||||
| 14 | C1a | 60 | 0 | 0 | 60 | 60 | 0 | 0 | 0 | 20 | 30 | 12 | 0 | 0 | 0 | = rhodoperihedron | ; | ||||
| 15 | C2a | 5 | 1 | 0 | 0 | 5 | 5 | 0 | 0 | 0 | 0 | 1 | 5 | 0 | 0 | = pentagonal pyramid | ; | ||||
| 16 | C3a | 3 | 0 | 1 | 3 | 0 | 0 | 3 | 0 | 1 | 0 | 0 | 0 | 3 | 0 | = tetrahedron | ; | ||||
| 17 | C4a | 8 | 4 | 2 | 4 | 4 | 8 | 8 | 2 | 0 | 2 | 0 | 4 | 4 | 4 | = bilunabirotunda | ; | ||||
| 18 | H4.1a | 120 | 24 | 20 | 120 | 120 | 120 | 120 | 12 | 40 | 60 | 24 | 120 | 120 | 60 | 2 | 24 | 40 | 30 | = castellated rhodoperihedral prism | ; |
Usage as facets
This polytope does not currently appear as facets in any higher-dimensional polytopes in the database.
Software models
| Notable Tetrashapes | |
| Regular: | pyrochoron • aerochoron • geochoron • xylochoron • hydrochoron • cosmochoron |
| Powertopes: | triangular octagoltriate • square octagoltriate • hexagonal octagoltriate • octagonal octagoltriate |
| Circular: | glome • cubinder • duocylinder • spherinder • sphone • cylindrone • dicone • coninder |
| Torii: | tiger • torisphere • spheritorus • torinder • ditorus |