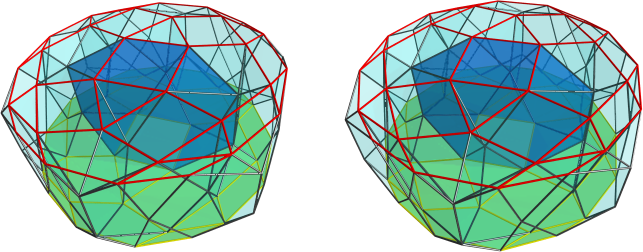Castellated rhodoperihedral prism (EntityTopic, 15)

From Hi.gher. Space

(Difference between revisions)
(created page)
m (CJ->BT)
 
(15 intermediate revisions not shown)
Line 1: Line 1:
-
<[#ontology [kind topic] [cats 4D Polytope]]>
+
<[#ontology [kind topic] [cats 4D Bilbirothawroid]]>
{{STS Shape
{{STS Shape
| dim=4
| dim=4
Line 6: Line 6:
| extra={{STS Polytope
| extra={{STS Polytope
}}}}
}}}}
-
 
+
The '''castellated rhodoperihedral prism''' is a [[bilbirothawroid]] discovered on February 4, 2014 by [[quickfur]] and confirmed by [[Klitzing]].[http://teamikaria.com/hddb/forum/viewtopic.php?p=20029#p20029] Although it is not strictly a [[prism]] (as it's not the [[Cartesian product]] of a base shape with a [[digon]]) it is so named as it has similar structure to "real" prisms of [[uniform polyhedra]].
-
The '''castellated rhodoperihedral prism''' is a [[crown jewel]] [[CRF polychoron]] discovered on February 4, 2014 by [[quickfur]] and confirmed by [[Klitzing]].[http://teamikaria.com/hddb/forum/viewtopic.php?p=20029#p20029] Although it is not strictly a [[prism]] (as it's not the [[Cartesian product]] of a base shape with a [[digon]]) it is so named as it has similar structure to "real" prisms of [[uniform polyhedra]].
+
Its cells are two [[rhodoperihedra]], 24 [[pentagonal pyramid]]s, 40 [[tetrahedra]] and 30 [[bilunabirotunda]]e (bilbiro). The rhodoperihedra form the "ends" of the prism, and are orthogonal to the bilbiro, which form the "sides" of the prism.
Its cells are two [[rhodoperihedra]], 24 [[pentagonal pyramid]]s, 40 [[tetrahedra]] and 30 [[bilunabirotunda]]e (bilbiro). The rhodoperihedra form the "ends" of the prism, and are orthogonal to the bilbiro, which form the "sides" of the prism.
Line 19: Line 18:
<blockquote>total edge length = 492''l''<br />
<blockquote>total edge length = 492''l''<br />
total surface area = (60 + 70√3 + 21√(25+10√5)) {{DotHV}}<br />
total surface area = (60 + 70√3 + 21√(25+10√5)) {{DotHV}}<br />
-
surcell volume = ''Unknown''<br />
+
surcell volume = {{Over|1|3}} &middot; (60φ<sup>2</sup> + 197φ + 74 + 10√2) {{DotHV|3}}<br />
bulk = ''Unknown''</blockquote>
bulk = ''Unknown''</blockquote>
-
{{Trishapes}}
+
== Projections ==
 +
Centered on a rhodoperihedron:
 +
 
 +
<[#embed [hash 08KY0A0ECHJZGX6MRP0ZPA10PQ]]>
 +
 
 +
Centered on a bilunabirotunda (J91):
 +
 
 +
<[#embed [hash T1GNP1B9G1V9T3MMEFSXY2B5G4]]>
 +
 
 +
== Coordinates ==
 +
The Cartesian coordinates of the castellated rhodoperihedral prism are:
 +
 
 +
{| class='wikitable'
 +
!Top and bottom x5o3x
 +
!Two &phi;<sup>2</sup>-scaled icosahedra
 +
!&phi;-scaled dodecahedron
 +
|-
 +
|
 +
:(±1, ±1, ±&phi;<sup>3</sup>, ±&phi;)
 +
:(±1, ±&phi;<sup>3</sup>, ±1, ±&phi;)
 +
:(±&phi;<sup>3</sup>, ±1, ±1, ±&phi;)
 +
:(±0, ±&phi;<sup>2</sup>, ±&phi;√5, ±&phi;)
 +
:(±&phi;<sup>2</sup>, ±&phi;√5, 0, ±&phi;)
 +
:(±&phi;√5, 0, ±&phi;<sup>2</sup>, ±&phi;)
 +
:(±&phi;, ±2&phi;, ±&phi;<sup>2</sup>, ±&phi;)
 +
:(±2&phi;, ±&phi;<sup>2</sup>, ±&phi;, ±&phi;)
 +
:(±&phi;<sup>2</sup>, ±&phi;, ±2&phi;, ±&phi;)
 +
|
 +
:(0, ±&phi;<sup>3</sup>, ±&phi;<sup>2</sup>, ±1)
 +
:(±&phi;<sup>3</sup>, ±&phi;<sup>2</sup>, 0, ±1)
 +
:(±&phi;<sup>2</sup>, 0, ±&phi;<sup>3</sup>, ±1)
 +
|
 +
:(±&phi;<sup>2</sup>, ±&phi;<sup>2</sup>, ±&phi;<sup>2</sup>, 0)
 +
:(±&phi;, ±&phi;<sup>3</sup>, 0, 0)
 +
:(±&phi;<sup>3</sup>, 0, ±&phi;, 0)
 +
:(0, ±&phi;, ±&phi;<sup>3</sup>, 0)
 +
|}
 +
 
 +
where &phi;=(1+√5)/2 is the Golden Ratio.
 +
 
 +
<[#polytope [id 71]]>
 +
 
 +
== Software models ==
 +
*[[Stella4D]] [http://hddb.teamikaria.com/dl/6SM4R1M4A1SGPDBVFMXW8740P6.off .off file]
 +
*[[Polyview]] [http://hddb.teamikaria.com/dl/XBNNJ2DBT0KSWT99BKPG08W49A.def .def file]
 +
 
 +
{{Tetrashapes}}

Latest revision as of 15:32, 1 March 2014

The castellated rhodoperihedral prism is a bilbirothawroid discovered on February 4, 2014 by quickfur and confirmed by Klitzing.[1] Although it is not strictly a prism (as it's not the Cartesian product of a base shape with a digon) it is so named as it has similar structure to "real" prisms of uniform polyhedra.

Its cells are two rhodoperihedra, 24 pentagonal pyramids, 40 tetrahedra and 30 bilunabirotundae (bilbiro). The rhodoperihedra form the "ends" of the prism, and are orthogonal to the bilbiro, which form the "sides" of the prism.

Its faces are 40 "end" triangles (x3o), 60 "end" squares (x2x), 24 "end" pentagons (o5x), 120 "lune-facing side" triangles (xo&#x), 120 "rotunda-facing side" triangles (xo&#x) and 60 "side" pentagons (ooooo3ooooo5ooooo&#xt).

It has 120 + 120 + 120 + 120 + 12 = 492 edges and 120 + 24 + 20 = 164 vertices.

Equations

  • The hypervolumes of a castellated rhodoperihedral prism with side length l are given by:
total edge length = 492l
total surface area = (60 + 70√3 + 21√(25+10√5)) · l2
surcell volume = 1∕3 · (60φ2 + 197φ + 74 + 10√2) · l3
bulk = Unknown

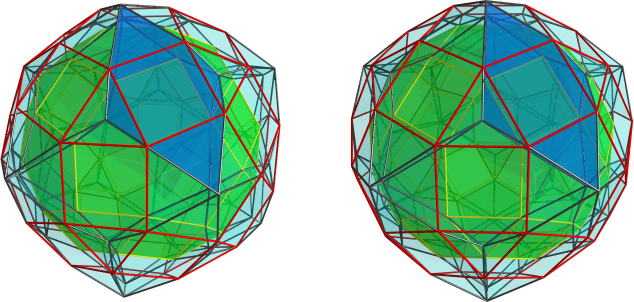
Projections

Centered on a rhodoperihedron:

(image)

Centered on a bilunabirotunda (J91):

(image)

Coordinates

The Cartesian coordinates of the castellated rhodoperihedral prism are:

Top and bottom x5o3x Two φ2-scaled icosahedra φ-scaled dodecahedron
(±1, ±1, ±φ3, ±φ)
(±1, ±φ3, ±1, ±φ)
(±φ3, ±1, ±1, ±φ)
(±0, ±φ2, ±φ√5, ±φ)
(±φ2, ±φ√5, 0, ±φ)
(±φ√5, 0, ±φ2, ±φ)
(±φ, ±2φ, ±φ2, ±φ)
(±2φ, ±φ2, ±φ, ±φ)
(±φ2, ±φ, ±2φ, ±φ)
(0, ±φ3, ±φ2, ±1)
(±φ3, ±φ2, 0, ±1)
(±φ2, 0, ±φ3, ±1)
(±φ2, ±φ2, ±φ2, 0)
(±φ, ±φ3, 0, 0)
(±φ3, 0, ±φ, 0)
(0, ±φ, ±φ3, 0)

where φ=(1+√5)/2 is the Golden Ratio.

Incidence matrix

Dual: D4.3.1 dual

#TXIDVaVbVcEaEbEcEdEe3a4a5a3b3c5bC1aC2aC3aC4aTypeName
0 Va = point ;
1 Vb = point ;
2 Vc = point ;
3 Ea 200 = digon ;
4 Eb 200 = digon ;
5 Ec 110 = digon ;
6 Ed 101 = digon ;
7 Ee 020 = digon ;
8 3a 30030000 = triangle ;
9 4a 40022000 = square ;
10 5a 50005000 = pentagon ;
11 3b 21001200 = triangle ;
12 3c 20110020 = triangle ;
13 5b 22100221 = pentagon ;
14 C1a 60006060000203012000 = rhodoperihedron ;
15 C2a 51005500001500 = pentagonal pyramid ;
16 C3a 30130030100030 = tetrahedron ;
17 C4a 84244882020444 = bilunabirotunda ;
18 H4.1a 120242012012012012012406024120120602244030 = castellated rhodoperihedral prism ;

Usage as facets

This polytope does not currently appear as facets in any higher-dimensional polytopes in the database.

Software models


Notable Tetrashapes
Regular: pyrochoron • aerochoron • geochoron • xylochoron • hydrochoron • cosmochoron
Powertopes: triangular octagoltriate • square octagoltriate • hexagonal octagoltriate • octagonal octagoltriate
Circular: glome • cubinder • duocylinder • spherinder • sphone • cylindrone • dicone • coninder
Torii: tiger • torisphere • spheritorus • torinder • ditorus
Retrieved from "http://hi.gher.space/wiki/Castellated_rhodoperihedral_prism"