Dicone (EntityTopic, 11)
From Hi.gher. Space
(Redirected from Rotope 38)
A dicone is a special case of a pyramid where the base is a cone. It is also a special case of a dipyramid where the base is a circle. It is bounded by two cones and an arrinder. Its faces are a circle and two curved-cone-surfaces.
Equations
- Variables:
r ⇒ radius of base of dicone
h ⇒ height of dicone
- The hypervolumes of a dicone are given by: (the red equations are thought to be inaccurate and need revising!)
total edge length = 2πr + h
total surface area = πr(r + 2√(r2 + h2))
surcell volume = πrh∕3 · (2r + √(r2 + h2))
bulk = π∕12 · r2h2
- The realmic cross-sections (n) of a dicone are:
Unknown
Cross-sections
Disk-first:
 Edge-first:
Edge-first:
 Cone-first:
Cone-first:

Projection
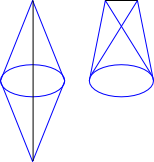
The following are the two possible types of parallel projections for a dicone:
The nappe-first parallel projection of the dicone into 3-space is a tetrahedron.
| Notable Tetrashapes | |
| Regular: | pyrochoron • aerochoron • geochoron • xylochoron • hydrochoron • cosmochoron |
| Powertopes: | triangular octagoltriate • square octagoltriate • hexagonal octagoltriate • octagonal octagoltriate |
| Circular: | glome • cubinder • duocylinder • spherinder • sphone • cylindrone • dicone • coninder |
| Torii: | tiger • torisphere • spheritorus • torinder • ditorus |
| 21. 1111 Triangular diprism | 22. 22 Dicone | 23. [11]2 Square dipyramid |
| List of tapertopes | ||