Tridiminished icosahedron (EntityTopic, 10)
From Hi.gher. Space
(Difference between revisions)
m (add symmetry group and Bowers acronym) |
(add relationship with J83) |
||
| Line 12: | Line 12: | ||
}}}} | }}}} | ||
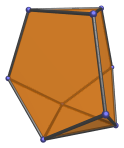
The '''tridiminished icosahedron''', abbreviated '''TDI''', is the 63rd [[Johnson solid]], J63. It suddenly became important when the [[bixylodiminished hydrochoron]] was discovered. It is the only CRF 3D member of the family of [[ursatope]]s, and appears as cells in the majority of the higher-dimensional ones. | The '''tridiminished icosahedron''', abbreviated '''TDI''', is the 63rd [[Johnson solid]], J63. It suddenly became important when the [[bixylodiminished hydrochoron]] was discovered. It is the only CRF 3D member of the family of [[ursatope]]s, and appears as cells in the majority of the higher-dimensional ones. | ||
| + | |||
| + | == Relationship with J83 == | ||
| + | It turns out that J83 is a kind of Stott expansion of J63. See the [[tridiminished rhodoperihedron]] page for the visualisation. | ||
== Equations == | == Equations == | ||
Revision as of 01:08, 12 March 2016
The tridiminished icosahedron, abbreviated TDI, is the 63rd Johnson solid, J63. It suddenly became important when the bixylodiminished hydrochoron was discovered. It is the only CRF 3D member of the family of ursatopes, and appears as cells in the majority of the higher-dimensional ones.
Relationship with J83
It turns out that J83 is a kind of Stott expansion of J63. See the tridiminished rhodoperihedron page for the visualisation.
Equations
- The hypervolumes of a tridiminished icosahedron with side length l are given by:
total edge length = 15l
surface area = 1∕4 · (3√(25+10√5) + 5√3) · l2
volume = (15+7√5)∕24 · l3
Incidence matrix
Dual: J63 dual
| # | TXID | Va | Vb | Vc | Ea | Eb | Ec | Ed | 3a | 5a | 3b | 3c | Type | Name |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Va | = point | ; top vertices | |||||||||||
| 1 | Vb | = point | ; mid vertices | |||||||||||
| 2 | Vc | = point | ; bot vertices | |||||||||||
| 3 | Ea | 2 | 0 | 0 | = digon | ; top to pen | ||||||||
| 4 | Eb | 1 | 1 | 0 | = digon | ; pen to pen | ||||||||
| 5 | Ec | 0 | 1 | 1 | = digon | ; pen to lat | ||||||||
| 6 | Ed | 0 | 0 | 2 | = digon | ; lat to bot | ||||||||
| 7 | 3a | 3 | 0 | 0 | 3 | 0 | 0 | 0 | = triangle | ; top | ||||
| 8 | 5a | 2 | 2 | 1 | 1 | 2 | 2 | 0 | = pentagon | ; pen | ||||
| 9 | 3b | 0 | 1 | 2 | 0 | 0 | 2 | 1 | = triangle | ; lat | ||||
| 10 | 3c | 0 | 0 | 3 | 0 | 0 | 0 | 3 | = triangle | ; bot | ||||
| 11 | C1a | 3 | 3 | 3 | 3 | 3 | 6 | 3 | 1 | 3 | 3 | 1 | = tridiminished icosahedron | ; |
Usage as facets
- 48× 1-facets of a bixylodiminished hydrochoron
- 96× 1-facets of a rectified snub demitesseract
- 96× 1-facets of a truncated snub demitesseract
- 32× 1-facets of a D4.11
- 12× 1-facets of a D4.7
| Notable Trishapes | |
| Regular: | tetrahedron • cube • octahedron • dodecahedron • icosahedron |
| Direct truncates: | tetrahedral truncate • cubic truncate • octahedral truncate • dodecahedral truncate • icosahedral truncate |
| Mesotruncates: | stauromesohedron • stauroperihedron • stauropantohedron • rhodomesohedron • rhodoperihedron • rhodopantohedron |
| Snubs: | snub staurohedron • snub rhodohedron |
| Curved: | sphere • torus • cylinder • cone • frustum • crind |