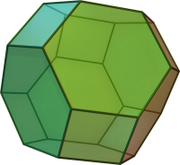
Octahedral truncate (EntityTopic, 11)
From Hi.gher. Space
The octahedral truncate is a particular uniform polyhedron. It is special because it is one of only five regular-faced convex polyhedra that can tile the realm (the others being the cube, triangular prism, hexagonal prism and gyrobifastigium).
Incidence matrix
Dual: tetrakis hexahedron
| # | TXID | Va | Ea | Eb | 4a | 6a | Type | Name |
|---|---|---|---|---|---|---|---|---|
| 0 | Va | = point | ; | |||||
| 1 | Ea | 2 | = digon | ; | ||||
| 2 | Eb | 2 | = digon | ; | ||||
| 3 | 4a | 4 | 0 | 4 | = square | ; | ||
| 4 | 6a | 6 | 3 | 3 | = hexagon | ; | ||
| 5 | C1a | 24 | 12 | 24 | 6 | 8 | = truncated octahedron | ; |
Usage as facets
This polytope does not currently appear as facets in any higher-dimensional polytopes in the database.
| Notable Trishapes | |
| Regular: | tetrahedron • cube • octahedron • dodecahedron • icosahedron |
| Direct truncates: | tetrahedral truncate • cubic truncate • octahedral truncate • dodecahedral truncate • icosahedral truncate |
| Mesotruncates: | stauromesohedron • stauroperihedron • stauropantohedron • rhodomesohedron • rhodoperihedron • rhodopantohedron |
| Snubs: | snub staurohedron • snub rhodohedron |
| Curved: | sphere • torus • cylinder • cone • frustum • crind |