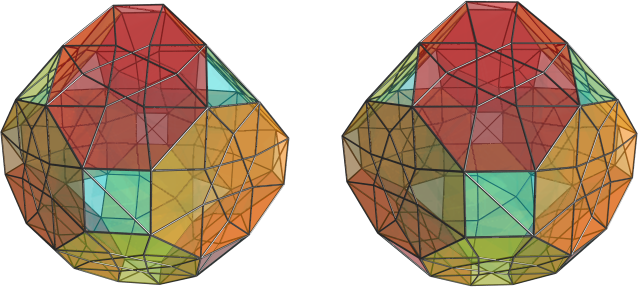D4.11 (EntityTopic, 13)
From Hi.gher. Space
D4.11 is a 4D CRF polychoron with 24 J91 cells in demitesseractic symmetry. It is related to D4.10 via a slight modification of its lace tower. Its cells are 8 stauromesohedra, 24 bilunabirotundae, 32 tridiminished icosahedra, 32+8=40 octahedra and 32+8=40 tetrahedra. Its faces are 96 pentagons, 48 squares and 32+96+32+32+96+96+32+32=448 triangles. It has 48+96+96+96+192+96=624 edges and 32+96+48=176 vertices.
Lace tower
x3o3o f3o3x o3x3f f3x3x x3F3o x3o3F F3x3o o3x3F F3o3x o3F3x x3x3f f3x3o x3o3f o3o3x
Projections
Centered on an axial tetrahedron:
Showing equatorial J91's:
Construction from snub demitesseract
D4.11 can also be constructed from the snub demitesseract in the following manner:
Firstly, write the snub demitesseract in its full demitesseractic symmetry as
x3o3o*b3f f3o3x*b3o o3o3f*b3x
Then, apply a caleido-faceting to the first node:
x3o3o*b3f -> (-x)3x3o*b3f f3o3x*b3o -> f3o3x*b3o o3o3f*b3x -> o3o3f*b3x
And finally, apply a partial Stott-expansion to the first node:
(-x)3o3o*b3f -> o3o3o*b3f
f3o3x*b3o -> F3o3x*b3o
o3o3f*b3x -> x3o3f*b3x
The result is D4.11, represented in full demitesseractic symmetry: oFx3ooo3oxf*b3fox&#zx.
Incidence matrix
Dual: D4.11 dual
| # | TXID | Va | Vb | Vc | Ea | Eb | Ec | Ed | Ee | Ef | 3a | 5a | 3b | 3c | 3d | 4a | 3e | 3f | 3g | 3h | C1a | C2a | C3a | C1b | C4a | C5a | C5b | Type | Name |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Va | = point | ; | ||||||||||||||||||||||||||
| 1 | Vb | = point | ; | ||||||||||||||||||||||||||
| 2 | Vc | = point | ; | ||||||||||||||||||||||||||
| 3 | Ea | 2 | 0 | 0 | = digon | ; | |||||||||||||||||||||||
| 4 | Eb | 1 | 1 | 0 | = digon | ; | |||||||||||||||||||||||
| 5 | Ec | 0 | 2 | 0 | = digon | ; | |||||||||||||||||||||||
| 6 | Ed | 0 | 2 | 0 | = digon | ; | |||||||||||||||||||||||
| 7 | Ee | 0 | 1 | 1 | = digon | ; | |||||||||||||||||||||||
| 8 | Ef | 0 | 0 | 2 | = digon | ; | |||||||||||||||||||||||
| 9 | 3a | 3 | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | = triangle | ; | |||||||||||||||||
| 10 | 5a | 2 | 2 | 1 | 1 | 2 | 0 | 0 | 2 | 0 | = pentagon | ; | |||||||||||||||||
| 11 | 3b | 1 | 2 | 0 | 0 | 2 | 1 | 0 | 0 | 0 | = triangle | ; | |||||||||||||||||
| 12 | 3c | 0 | 3 | 0 | 0 | 0 | 3 | 0 | 0 | 0 | = triangle | ; | |||||||||||||||||
| 13 | 3d | 0 | 3 | 0 | 0 | 0 | 0 | 3 | 0 | 0 | = triangle | ; | |||||||||||||||||
| 14 | 4a | 0 | 4 | 0 | 0 | 0 | 2 | 2 | 0 | 0 | = square | ; | |||||||||||||||||
| 15 | 3e | 0 | 1 | 2 | 0 | 0 | 0 | 0 | 2 | 1 | = triangle | ; | |||||||||||||||||
| 16 | 3f | 0 | 2 | 1 | 0 | 0 | 0 | 1 | 2 | 0 | = triangle | ; | |||||||||||||||||
| 17 | 3g | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 3 | = triangle | ; | |||||||||||||||||
| 18 | 3h | 0 | 0 | 3 | 0 | 0 | 0 | 0 | 0 | 3 | = triangle | ; | |||||||||||||||||
| 19 | C1a | 4 | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | = tetrahedron | ; | |||||||
| 20 | C2a | 3 | 3 | 3 | 3 | 3 | 0 | 0 | 6 | 3 | 1 | 3 | 0 | 0 | 0 | 0 | 3 | 0 | 1 | 0 | = tridiminished icosahedron | ; | |||||||
| 21 | C3a | 4 | 8 | 2 | 2 | 8 | 4 | 4 | 8 | 0 | 0 | 4 | 4 | 0 | 0 | 2 | 0 | 4 | 0 | 0 | = bilunabirotunda | ; | |||||||
| 22 | C1b | 1 | 3 | 0 | 0 | 3 | 3 | 0 | 0 | 0 | 0 | 0 | 3 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | = tetrahedron | ; | |||||||
| 23 | C4a | 0 | 12 | 0 | 0 | 0 | 12 | 12 | 0 | 0 | 0 | 0 | 0 | 4 | 4 | 6 | 0 | 0 | 0 | 0 | = stauromesohedron | ; | |||||||
| 24 | C5a | 0 | 3 | 3 | 0 | 0 | 0 | 3 | 6 | 3 | 0 | 0 | 0 | 0 | 1 | 0 | 3 | 3 | 0 | 1 | = octahedron | ; | |||||||
| 25 | C5b | 0 | 0 | 6 | 0 | 0 | 0 | 0 | 0 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 4 | 4 | = octahedron | ; | |||||||
| 26 | H4.1a | 32 | 96 | 48 | 48 | 96 | 96 | 96 | 192 | 96 | 32 | 96 | 96 | 32 | 32 | 48 | 96 | 96 | 32 | 32 | 8 | 32 | 24 | 32 | 8 | 32 | 8 | = D4.11 | ; |
Usage as facets
This polytope does not currently appear as facets in any higher-dimensional polytopes in the database.