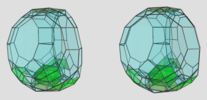
Ursatope (EntityClass, 8)
From Hi.gher. Space
The ursatopes are bistratic polytopes that may be constructed from any polytope P. P with unit edge length, P scaled by the golden ratio, and rectified P with unit edge length, are placed in three parallel hyperplanes, the relative heights of which are adjusted such that vertices from the three layers line up to form pentagons. The convex hull of these three layers of vertices will be a polytope that has P as the top cell, rectified P as the bottom cell, and lower-dimensional ursatopes and pyramids lacing the two. If the resulting edge lengths are equal, the result will be a CRF (convex regular-faced) polytope.
History
In 2004 Andrew Weimholt discovered a bistratic polychoron constructed from the convex hull of a unit tetrahedron, a tetrahedron scaled by the golden ratio, and a unit octahedron. It consists of 4 tridiminished icosahedra surrounding a tetrahedron, with 4 more tetrahedra on the other end connecting the tridiminished icosahedra to an octahedron. This shape is in fact a 4D analog of the tridiminished icosahedron itself, which has been nicknamed "Teddy" by Klitzing (from Jonathan Bowers' acronym for the tridiminished icosahedron: teddi), a name which was quickly adopted by quickfur, although there is some confusion about the dimensions. Weimholt then even showed that this type of figure runs through all dimensions.
Subsequently, a whole class of similar shapes have been discovered, all containing tridiminished icosahedra, which may be referred to as ursatopes (a pun on "teddy").
Wendy Krieger elaborated Weimholt's result to a broader base: As base might serve any quasiregular polytope (just a single node of its Dynkin diagram being ringed), provided the links to that node are marked 3 only (posessing only triangular 2D-faces), and the circumradius of that quasiregular base is less than the Golden Ratio f=1.618. The next vertex layer then would be described again by the scaled version of the bottom, scaling factor being f. This one features just as pseudo face, or cross-section. The top layer finally will be the rectified version of the bottom face, i.e. its Dynkin diagram rings all neighbours of the former singularily ringed node, but un-rings that very one. (Conway-Hart rule.) The total ursatope happens to be the hull of that axial stack.
Moreover it was shown that all these ursatopes then will be orbiform (all vertices on a single hypersphere).
List of ursatopes
In 2D, there is one ursatope: the digonal ursagon, which is the same as a pentagon.
In 3D, there is one CRF ursatope: the trigonal ursahedron, which is the same as the tridiminished icosahedron.
The other ursahedra, such as the square ursahedron and the pentagonal ursahedron (which is a diminished dodecahedron), are not CRF.
In 4D, there are three known CRF ursatopes:
- The pyroursachoron xfo3oox3ooo
 , with 5 tetrahedra, one octahedron and 4 tridiminished icosahedra;
, with 5 tetrahedra, one octahedron and 4 tridiminished icosahedra;
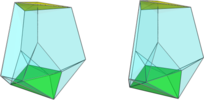
- The aeroursachoron xfo3oox4ooo
 , with an octahedron, a cuboctahedron, 8 tridiminished icosahedra and 6 square pyramids;
, with an octahedron, a cuboctahedron, 8 tridiminished icosahedra and 6 square pyramids;
- The hydroursachoron xfo3oox5ooo
 , with an icosahedron, an icosidodecahedron, 20 tridiminished icosahedra and 12 pentagonal pyramids.
, with an icosahedron, an icosidodecahedron, 20 tridiminished icosahedra and 12 pentagonal pyramids.
Other ursachora are possible, but it is believed that they are not CRF.
In 5D, there are believed to be the following CRF ursatopes:
- The pyroursateron, with 6 pyrochora, one rectified pyrochoron, and five pyroursachora.
- The aeroursateron, with an aerochoron, a xylochoron, 16 pyroursachora, and 8 octahedral pyramids.
- The xyloursateron, with a xylochoron, a rectified xylochoron, 24 aeroursachora, and 24 cubical pyramids.
- The hydroursateron, with a hydrochoron, a rectified hydrochoron, 600 pyroursachora, and 120 icosahedral pyramids.
In all higher dimensions n > 5, only two CRF ursatopes are believed possible:
- The pyroursatope: (n+1) pyro-(n-1)-topes, a rectified pyro-(n-1)-tope and n pyroursa-(n-1)-topes;
- The aeroursatope: an aero-(n-1)-tope, a rectified aero-(n-1)-tope, 2n-1 pyroursa-(n-1)-topes and (2n-2) aero-(n-2)-tope pyramids.
Expanded ursatopes
Expanded ursatopes may be constructed by expanding the facets of the top facet such that the ursatope facets are pushed apart. Prisms are inserted between the ursatope facets, causing the bottom facet to also expand, and the lacing pyramids to expand into cupolae. Expanded ursatopes may be used to construct higher-dimensional modified ursatopes in which the lacing facets are expanded ursatopes, etc.
Each of the three ursachora have corresponding expanded forms:
- The expanded pyroursachoron xfo3oox3xxx, with a cuboctahedron, a truncated octahedron, 4 tridiminished icosahedra, 6 pentagonal prisms, 4 triangular prisms and 4 triangular cupola (to be verified);
- The expanded aeroursachoron xfo3oox4xxx
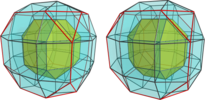 , with a rhombicuboctahedron, a truncated cube, 8 tridiminished icosahedra, 12 pentagonal prisms, 6 cubes and 6 square cupola;
, with a rhombicuboctahedron, a truncated cube, 8 tridiminished icosahedra, 12 pentagonal prisms, 6 cubes and 6 square cupola;
- The expanded hydroursachoron xfo3oox5xxx, with a rhombicosidodecahedron, a truncated dodecahedron, 20 tridiminished icosahedra, 30+12 = 42 pentagonal prisms and 12 pentagonal cupola (to be verified).
Magnaursatopes
In March 2016, User:Quickfur discovered that it is possible to construct a 4D analogue of the tridiminished rhombicosidodecahedron (J83) using a similar construction to the ursatopes. This has been assigned D4.15 and is currently informally referred to as the magnaursachoron:
It is surmised that higher-dimensional analogues are possible, using lower-dimensional ursatopes (including the above magnaursachoron) as facets. However, this has yet to be verified.
Currently, it is believed that analogues of this (tetrahedral) magnaursachoron with octahedral or icosahedral symmetry cannot be CRF, as the construction would require 3D ursahedra with square / pentagonal symmetry, which are non-CRF.
Augmented ursatopes
3D
In 3D, the tridiminished icosahedron can be augmented with a tetrahedron to produce the Johnson solid augmented tridiminished icosahedron (J64).
4D
In July 2016, it was discovered that 4D analogues of J64 exist:
- The tetrahedral, octahedral, and icosahedral ursachora can be augmented, respectively, with a 5-cell, an octahedral pyramid, or an icosahedral pyramid to form augmented ursachora.
- Moreoever, the lateral tridiminished icosahedral cells of these ursachora can also be augmented with tridiminished icosahedral pyramids. These lateral augments would cause the polytope to become concave if used simultaneously with the previous "top-cell" augments; in the case of the icosahedral ursachoron, the concave portions can be made convex again by inserting pentagonal pyramid pyramids, producing a fragment of the surface of the 600-cell. However, no such remedy can be made for the tetrahedral and octahedral ursachora. Therefore, for these two ursachora only one or the other kind of augments can added while remaining CRF.
The following cases are known:
- Top-augmented tetrahedral ursachoron (verified to be CRF)
- Laterally-augmented tetrahedral ursachoron: up to 4 augments can be added (the tetra-augmented tetrahedral ursachoron has been verified to be CRF).
- Top-augmented octahedral ursachoron (verified to be CRF)
- Laterally-augmented octahedral ursachoron: only non-adjacent augments are admissible, because the greater dichoral angles in the octahedral ursachoron would cause concave gaps to appear between adjacent augments. The maximal augmentation therefore is 4 augments in tetrahedral symmetry. With 3 augments or less, there are multiple possible configurations, corresponding with the number of subsets of non-adjacent faces of the octahedron, modulo octahedral symmetry. (The tetra-augmented octahedral ursachoron has been verified to be CRF.)
- Top-augmented icosahedral ursachoron (to be verified -- but almost certainly CRF because it corresponds with a diminishing of the 600-cell)
- Laterally-augmented icosahedral ursachoron (to be verified -- these are non-convex but have CRF convex hulls corresponding with fragments of the 600-cell's surface).
5D and beyond
It is surmised, though not yet rigorously proven, that top-augmented n-simplex ursatopes ought to exist in all dimensions ≥ 3.
Richard Klitzing found that the tetrahedral ursachoron is orbiform with a radius of 1, which implies that the 5D tetrahedral ursachoron pyramid would be degenerate (zero-height). This seems to indicate that laterally-augmented ursatopes probably do not exist in 5D and beyond, and consequently laterally-augmented ursatopes likely also do not exist beyond 4D.