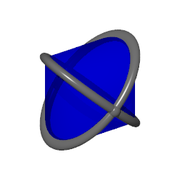
Crind (EntityTopic, 10)
From Hi.gher. Space
A crind is the intersection of two perpendicular cylinders. Due to momentum it will behave similarly to a duocylinder if left to roll on a surface. However, unlike a duocylinder, a crind can be stopped and then rolled in a different direction without needing to rotate it.
The crind is also one of the few curved polyhedra that satisfies Euler's F + V = E + 2.
Its maximal and minimal compressions are an irregular octahedron and a line segment respectively.
Equations
- Assumption: Crind is centered at the origin.
- Variables:
r ⇒ radius of crind
- All points (x, y, z) that lie on the surface of a crind will satisfy the following equations:
x + y ≤ x + z = r
-- or --
x + z ≤ x + y = r
- All points (x, y, z) that lie on the edges of a crind will satisfy the following equation:
x + y = x + z = r
- The hypervolumes of a crind are given by:
total edge length = 4πsqrt(2)r
surface area = Unknown
volume = πr3
- The planar cross-sections (n) of a crind are:
[!x,!y] ⇒ circle [!z] ⇒ square
- The radial slices θ of a crind are:
[x:xy,x:xz] ⇒ ellipse with major radius rsin(45° + (θ % 90°)√2 and minor radius r
[y:xy,y:yz,z:xz,z:yz] ⇒ "circle with ends cut" of unknown proportions
| Notable Trishapes | |
| Regular: | tetrahedron • cube • octahedron • dodecahedron • icosahedron |
| Direct truncates: | tetrahedral truncate • cubic truncate • octahedral truncate • dodecahedral truncate • icosahedral truncate |
| Mesotruncates: | stauromesohedron • stauroperihedron • stauropantohedron • rhodomesohedron • rhodoperihedron • rhodopantohedron |
| Snubs: | snub staurohedron • snub rhodohedron |
| Curved: | sphere • torus • cylinder • cone • frustum • crind |
| 8. <(II)I> Bicone | 9. ([II]I) Crind | 10. [IIII] Geochoron |
| List of bracketopes | ||