Bicone (EntityTopic, 10)
From Hi.gher. Space
(Difference between revisions)
(New page: {{STS Shape | image=http://teamikaria.com/dl/zUBp_NLApjYHqsS_nfADWUzetvnDL4sSf5B2Gi2pc4-ygOKY.png | dim=3 | elements=2, 1, 2 | genus=0 | ssc=<(xy)z> | ssc2=T2vM1 | extra={{STS Bracketope |...) |
Username5243 (Talk | contribs) (→Equations) |
||
| (5 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| + | <[#ontology [kind topic] [cats 3D Bracketope Curved]]> | ||
{{STS Shape | {{STS Shape | ||
| - | | image= | + | | image=<[#embed [hash RQBYTBGJKTVCMV1MDFX1TTA2C5] [width 180]]> |
| dim=3 | | dim=3 | ||
| - | | elements=2, 1, 2 | + | | elements=2 conic naps, 1 circular edge, 2 [[point]]s |
| genus=0 | | genus=0 | ||
| ssc=<(xy)z> | | ssc=<(xy)z> | ||
| ssc2=T2vM1 | | ssc2=T2vM1 | ||
| extra={{STS Bracketope | | extra={{STS Bracketope | ||
| - | | index= | + | | index=8 |
| + | | notation=<(II)I> | ||
}}}} | }}}} | ||
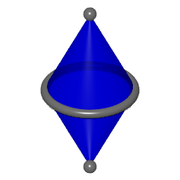
| - | A '''bicone''' is the [[tegum product]] of a [[circle]] and a [[digon]]. | + | A '''bicone''' is the [[tegum product]] of a [[circle]] and a [[digon]]. It is also the result of attaching two [[cone]]s at their bases. |
| + | == Equations == | ||
| + | *Variables: | ||
| + | <blockquote>''r'' ⇒ radius of base of bicone<br> | ||
| + | ''h'' ⇒ perpendicular height of bicone from the circle to one of the vertices</blockquote> | ||
| + | |||
| + | *The [[hypervolume]]s of a bicone are given by: | ||
| + | <blockquote>total edge length = 2π''r''<br> | ||
| + | surface area = 2π''r''√(''r''<sup>2</sup> + ''h''<sup>2</sup>))<br> | ||
| + | volume = {{Over|2π|3}} · ''r''<sup>2</sup>''h''</blockquote> | ||
| + | |||
| + | *The [[planar]] [[cross-section]]s (''n'') of a cone are: | ||
| + | <blockquote>[!x,!y] ⇒ rhombus <br> | ||
| + | [!z] ⇒ circle | ||
| + | </blockquote> | ||
{{Trishapes}} | {{Trishapes}} | ||
| - | {{Bracketope Nav| | + | {{Bracketope Nav|7|8|9|[(II)I]<br>Cylinder|<(II)I><br>Bicone|([II]I)<br>Crind|hedra}} |
Latest revision as of 15:03, 26 March 2017
A bicone is the tegum product of a circle and a digon. It is also the result of attaching two cones at their bases.
Equations
- Variables:
r ⇒ radius of base of bicone
h ⇒ perpendicular height of bicone from the circle to one of the vertices
- The hypervolumes of a bicone are given by:
total edge length = 2πr
surface area = 2πr√(r2 + h2))
volume = 2π∕3 · r2h
- The planar cross-sections (n) of a cone are:
[!x,!y] ⇒ rhombus
[!z] ⇒ circle
| Notable Trishapes | |
| Regular: | tetrahedron • cube • octahedron • dodecahedron • icosahedron |
| Direct truncates: | tetrahedral truncate • cubic truncate • octahedral truncate • dodecahedral truncate • icosahedral truncate |
| Mesotruncates: | stauromesohedron • stauroperihedron • stauropantohedron • rhodomesohedron • rhodoperihedron • rhodopantohedron |
| Snubs: | snub staurohedron • snub rhodohedron |
| Curved: | sphere • torus • cylinder • cone • frustum • crind |
| 7. [(II)I] Cylinder | 8. <(II)I> Bicone | 9. ([II]I) Crind |
| List of bracketopes | ||