Manifold (ConceptTopic, 4)
From Hi.gher. Space
A manifold is a topological object which locally resembles Euclidean space. Manifolds may or may not have boundaries and may or may not be orientable.
Nullar and linear manifolds
The manifolds in 0D and 1D are relatively trivial, but are included for completeness:
| nullar | linear | |
|---|---|---|
| Point | Line segment | Circle |
The colored boundaries (for the circle, the two red points) must be identified to form the desired manifold.
Planar manifolds
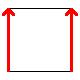
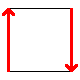
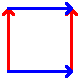
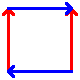
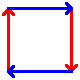
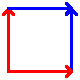
These are the best known manifolds. There are seven "interesting" ones, shown below:
| Group 0 | Group 1 | Group 2 | ||||
|---|---|---|---|---|---|---|
| Disc | Hose (uncapped cylinder) | Möbius strip | Torus | Klein bottle | Real projective plane | Sphere |

| 
| 
| 
| 
| 
| 
|
To construct, connect up the colored edges so that the colors and arrowheads match.
There are infinitely many more such manifolds in group 2, one each of the orientable and non-orientable varieties for each possible genus. Only the possibilities for genus 0 and 1 are shown above.
Cubic manifolds
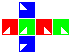
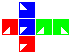
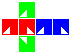
Some examples are shown in the following table.
| Group 0-0 | Group 1-0 | Group 2-0 | Group 3-0 | Group 0-2 | Group 1-2 | Group 0-3 | |
|---|---|---|---|---|---|---|---|
| Cube | Dihose | Toric hose | Ditorus | Spherical hose | Glome | Torisphere | Torispheric bottle |

| 
| 
| 
| 
| 
| 
| 
|
| Möbial hose | Real projective planar hose | Toric bottle | |||||

| 
| 
| |||||
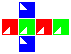
| Real projective realm | |||||||
| |||||||
Construction is similar to that of the square manifolds: fold up each cubic net and attach the red, blue and green pairs of facets to each other in that order, making sure the triangles line up.
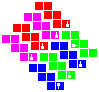
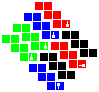
Tesseric manifolds
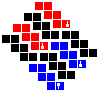
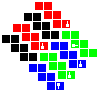
Here are the 4D p-toric q-hoses and p-spheric q-hoses along with the tesseract and möbial dihose:
| Group 0-0 | Group 1-0 | Group 2-0 | Group 3-0 | Group 4-0 | Group 0-2 | Group 0-3 | Group 0-4 | |
|---|---|---|---|---|---|---|---|---|
| Tesseract | Möbial dihose | Trihose | Toric dihose | Ditoric hose | Tritorus | Spherical dihose | Glomic hose | Pentasphere |

| 
| 
| 
| 
| 
| 
| 
| 
|
| I | 1 | 0 | 00 | 000 | 0000 | SS | SSS | SSSS |
To construct, first fold up the nets for each cube and attach the cubes into the net of a tesseract as shown below, making sure to preserve orientation. Solidify the tesseract net and fold that up too. Then, attach the red, blue, green and yellow pairs of facets to each other in that order, lining up the symbols.

