Manifold (ConceptTopic, 4)

From Hi.gher. Space

(Difference between revisions)
m (→Cubic manifolds: fix!)
m (ontology)
 
(13 intermediate revisions not shown)
Line 1: Line 1:
-
A '''manifold''' is a [[shape]] formed from a [[regular]] base shape, where various edges are connected either with or without twists.
+
<[#ontology [kind topic] [cats Essays Topology]]>
 +
A '''manifold''' is a topological object which locally resembles Euclidean space. Manifolds may or may not have boundaries and may or may not be orientable.
-
== Square manifolds ==
+
== Nullar and linear manifolds ==
 +
The manifolds in 0D and 1D are relatively trivial, but are included for completeness:
-
These are the best known manifolds. There are eight of them shown as follows:
+
{|
 +
!style="background-color: #EEE;"|nullar
 +
!style="background-color: #EEE;" colspan="2"|linear
 +
|-
 +
|width="33%" align="center"|[[Point]]
 +
|width="33%" align="center"|[[Line segment]]
 +
|width="33%" align="center"|[[Circle]]
 +
|-
 +
|align="center"|<[#embed [hash P766YK46JBQDMRHN08FCGDWC0B]]>
 +
|align="center"|<[#embed [hash 76ARJ0KWJPGETCCXSNWQ813V9M]]>
 +
|align="center"|<[#embed [hash KBTKCV8P4Q8ETDE2WSJGTZKFRF]]>
 +
|}
 +
 
 +
The colored boundaries (for the circle, the two red points) must be identified to form the desired manifold.
 +
 
 +
== Planar manifolds ==
 +
 
 +
These are the best known manifolds. There are seven "interesting" ones, shown below:
{|
{|
-
!style="background-color: #EEE;"|Group I0
+
!style="background-color: #EEE;"|Group 0
-
!colspan="2" style="background-color: #EEE;"|Group I1
+
!colspan="2" style="background-color: #EEE;"|Group 1
-
!colspan="4" style="background-color: #EEE;"|Group I2
+
!colspan="4" style="background-color: #EEE;"|Group 2
-
!style="background-color: #EEE;"|Group S2
+
|-
|-
-
|width="12%" align="center"|[[Square]]
+
|width="12%" align="center"|[[Disc]]
|width="12%" align="center"|[[Hose]] (uncapped [[cylinder]])
|width="12%" align="center"|[[Hose]] (uncapped [[cylinder]])
|width="12%" align="center"|[[Möbius strip]]
|width="12%" align="center"|[[Möbius strip]]
|width="12%" align="center"|[[Torus]]
|width="12%" align="center"|[[Torus]]
-
|width="12%" align="center"|[[Klein figure 8]]
 
|width="12%" align="center"|[[Klein bottle]]
|width="12%" align="center"|[[Klein bottle]]
|width="12%" align="center"|[[Real projective plane]]
|width="12%" align="center"|[[Real projective plane]]
|width="12%" align="center"|[[Sphere]]
|width="12%" align="center"|[[Sphere]]
|-
|-
-
|align="center"|http://teamikaria.com/dl/zebnuw8TVYvi5oa7PHJFVXjeWIzl6j5b_OqpV9YRZnQ1HR5q.png
+
|align="center"|<[#embed [hash 0EX1WDTD1B3KTWDXB98FPQG26T]]>
-
|align="center"|http://teamikaria.com/dl/HGJdxDSgKdFFmJwMx3NmaeeTiQYuIdQTfVqyhFLWxV8c60WH.png
+
|align="center"|<[#embed [hash 41F6MQT3MFYRRKNQBBSKWWX4FG]]>
-
|align="center"|http://teamikaria.com/dl/iCJxkx0R_t4XE_yO1bF8QpBRH-XMi5nDn-ELIknrjyQDa9X8.png
+
|align="center"|<[#embed [hash GXSMG22779KTTFH16Q81TQXF36]]>
-
|align="center"|http://teamikaria.com/dl/K0bGhfOG3hetb1QT2ev6gCwfdT_JioJJVxSOe65WDn2pyrQW.png
+
|align="center"|<[#embed [hash EK4R8ABYEP6YCVZKM4QMJKC3S5]]>
-
|align="center"|http://teamikaria.com/dl/LpJNtb-p34CMW2XuXAEHxPWu_Yo2bx-gXbyxr8eOQU8xdJAr.png
+
|align="center"|<[#embed [hash ZC0PJNBY5BZZEHD8Q6A3TZHBYX]]>
-
|align="center"|http://teamikaria.com/dl/GonihCjgciwA83T8wiya7qsB93p4mpXIi2_t-EWe11UwKv71.png
+
|align="center"|<[#embed [hash QY2NW8J9RCC9CK6GBPF3AZ01D0]]>
-
|align="center"|http://teamikaria.com/dl/4h4Ag96nOfc3GRzA8r_rwcqoGURpR8NFiLFWJ9VogyAGV2az.png
+
|align="center"|<[#embed [hash 62XZYY54QA05YXTE878CGPAPJ5]]>
-
|align="center"|http://teamikaria.com/dl/6DfUWpRUCTvIcPzgXCfjaVzgQueSMNorAmgm8o87JArm5GhR.png
+
-
|-
+
-
|align="center"|I
+
-
|align="center"|0
+
-
|align="center"|1
+
-
|align="center"|00
+
-
|align="center"|01
+
-
|align="center"|10
+
-
|align="center"|11
+
-
|align="center"|SS
+
|}
|}
-
To construct, first connect the red edges to each other, matching up the arrowheads, and then connect the blue arrows together in the same way. Edges without arrows are left unconnected.
+
To construct, connect up the colored edges so that the colors and arrowheads match.
-
The Klein figure 8 and Klein bottle are topologically equivalent, however they have been listed separately as they appear significantly different.
+
There are infinitely many more such manifolds in group 2, one each of the orientable and non-orientable varieties for each possible genus. Only the possibilities for genus 0 and 1 are shown above.
== Cubic manifolds ==
== Cubic manifolds ==
-
There are 279 unique cubic manifolds out of 611 defined ones. Only sufficient examples and the most interesting are shown in the following table.
+
Some examples are shown in the following table.
{|
{|
-
!style="background-color: #EEE;"|Group I0
+
!style="background-color: #EEE;"|Group 0-0
-
!style="background-color: #EEE;"|Group I1
+
!style="background-color: #EEE;"|Group 1-0
-
!style="background-color: #EEE;"|Group I2
+
!style="background-color: #EEE;"|Group 2-0
-
!style="background-color: #EEE;" colspan="2"|Group I3
+
!style="background-color: #EEE;"|Group 3-0
-
!style="background-color: #EEE;"|Group S2
+
!style="background-color: #EEE;"|Group 0-2
-
!style="background-color: #EEE;" colspan="2"|Group S3
+
!style="background-color: #EEE;"|Group 1-2
-
|-
+
!style="background-color: #EEE;" colspan="2"|Group 0-3
-
|align="center"|1 defined
+
-
|align="center"|8 defined
+
-
|align="center"|64 defined
+
-
|align="center" colspan="2"|512 defined
+
-
|align="center"|1 defined
+
-
|align="center" colspan="2"|25 defined
+
-
|-
+
-
|align="center"|1 unique
+
-
|align="center"|6 unique
+
-
|align="center"|36 unique
+
-
|align="center" colspan="2"|216 unique
+
-
|align="center"|1 unique
+
-
|align="center" colspan="2"|19 unique
+
-
|-
+
-
|align="center"|1 shown
+
-
|align="center"|2 shown
+
-
|align="center"|2 shown
+
-
|align="center" colspan="2"|3 shown
+
-
|align="center"|1 shown
+
-
|align="center" colspan="2"|4 shown
+
|-
|-
|align="center" width="12%"|[[Cube]]
|align="center" width="12%"|[[Cube]]
Line 80: Line 67:
|align="center" width="12%"|[[Toric hose]]
|align="center" width="12%"|[[Toric hose]]
|align="center" width="12%"|[[Ditorus]]
|align="center" width="12%"|[[Ditorus]]
-
|align="center" width="12%"|[[Toric bottle]]
 
|align="center" width="12%"|[[Spherical hose]]
|align="center" width="12%"|[[Spherical hose]]
-
|align="center" width="12%"|[[Toraspherinder]]
 
|align="center" width="12%"|[[Glome]]
|align="center" width="12%"|[[Glome]]
 +
|align="center" width="12%"|[[Torisphere]]
 +
|align="center" width="12%"|[[Torispheric bottle]]
 +
|-
 +
|align="center"|<[#embed [hash W7W6JRCG1GHCAHH1N2KP2N1NCM]]>
 +
|align="center"|<[#embed [hash 1GWNWDNN81JJEDJNVWVZMM3QHV]]>
 +
|align="center"|<[#embed [hash 0GK7JFAJ2XQAMKWXH3TCMJCP71]]>
 +
|align="center"|<[#embed [hash TVCAYEY97PY08SK3PV5CWNY5TG]]>
 +
|align="center"|<[#embed [hash FQYQTJB0M7HW4APZJ89YAZM6RS]]>
 +
|align="center"|<[#embed [hash 4EC5W3YCRSJEPV6BGPXKY18VT8]]>
 +
|align="center"|<[#embed [hash R2GEAJMABF01MCPMD04GPYAZV5]]>
 +
|align="center"|<[#embed [hash 83VKP6HCJ7350SJHQ3KY07HWA5]]>
|-
|-
|align="center"|
|align="center"|
|align="center"|[[Möbial hose]]
|align="center"|[[Möbial hose]]
|align="center"|[[Real projective planar hose]]
|align="center"|[[Real projective planar hose]]
 +
|align="center"|[[Toric bottle]]
 +
|align="center"|
 +
|align="center"|
 +
|align="center"|
 +
|align="center"|
 +
|-
 +
|align="center"|
 +
|align="center"|<[#embed [hash TX5MJ1WCM20KR7YHS91GWB6H0R]]>
 +
|align="center"|<[#embed [hash 395RTJ36APYXM3K4HTT0EB9WAV]]>
 +
|align="center"|<[#embed [hash 19RGPZ3XGR1NJNTCTJW7WENYKE]]>
 +
|align="center"|
 +
|align="center"|
 +
|align="center"|
 +
|align="center"|
 +
|-
 +
|align="center"|
 +
|align="center"|
 +
|align="center"|
|align="center"|[[Real projective realm]]
|align="center"|[[Real projective realm]]
|align="center"|
|align="center"|
|align="center"|
|align="center"|
-
|align="center"|[[Toraspherindric bottle]]
+
|align="center"|
-
|align="center"|[[Toraspherindric dalma]]
+
|align="center"|
 +
|-
 +
|align="center"|
 +
|align="center"|
 +
|align="center"|
 +
|align="center"|<[#embed [hash 4HNZC40T26JRPN1DNB67WVWP9X]]>
 +
|align="center"|
 +
|align="center"|
 +
|align="center"|
 +
|align="center"|
|}
|}
-
[[Category:Topology]]
+
Construction is similar to that of the square manifolds: fold up each cubic net and attach the red, blue and green pairs of facets to each other in that order, making sure the triangles line up.
 +
 
 +
== Tesseric manifolds ==
 +
 
 +
Here are the 4D ''p''-toric ''q''-hoses and ''p''-spheric ''q''-hoses along with the tesseract and möbial dihose:
 +
 
 +
{|
 +
!style="background-color: #EEE;"|Group 0-0
 +
!style="background-color: #EEE;" colspan="2"|Group 1-0
 +
!style="background-color: #EEE;"|Group 2-0
 +
!style="background-color: #EEE;"|Group 3-0
 +
!style="background-color: #EEE;"|Group 4-0
 +
!style="background-color: #EEE;"|Group 0-2
 +
!style="background-color: #EEE;"|Group 0-3
 +
!style="background-color: #EEE;"|Group 0-4
 +
|-
 +
|align="center" width="11%"|[[Tesseract]]
 +
|align="center" width="11%"|[[Möbial dihose]]
 +
|align="center" width="11%"|[[Trihose]]
 +
|align="center" width="11%"|[[Toric dihose]]
 +
|align="center" width="11%"|[[Ditoric hose]]
 +
|align="center" width="11%"|[[Tritorus]]
 +
|align="center" width="11%"|[[Spherical dihose]]
 +
|align="center" width="11%"|[[Glomic hose]]
 +
|align="center" width="11%"|[[Pentasphere]]
 +
|-
 +
|align="center"|<[#embed [hash 9G7AM9VEHMV1W01WCJ0CM94Z9Y]]>
 +
|align="center"|<[#embed [hash R7DDJV8RQAPDMMMYKQMVRJNQZB]]>
 +
|align="center"|<[#embed [hash 4J2PPH2RD1N0R49YXGT8YRW24W]]>
 +
|align="center"|<[#embed [hash YAY0W92CT89Z0NP84YACRKTVPH]]>
 +
|align="center"|<[#embed [hash 8BVY4XJSZ8MTCEBCZ6CXWF25EC]]>
 +
|align="center"|<[#embed [hash 0TR3G55XEAQCWYC4M3NBTRASTT]]>
 +
|align="center"|<[#embed [hash 3GPR6AT6K99QTAVM3TJNYR90P6]]>
 +
|align="center"|<[#embed [hash RE2MT4CJAN7PRSZ32F5QWAN5GD]]>
 +
|align="center"|<[#embed [hash EQAFRCZ9KPKVJACAE4KCG35KV2]]>
 +
|-
 +
|align="center"|I
 +
|align="center"|1
 +
|align="center"|0
 +
|align="center"|00
 +
|align="center"|000
 +
|align="center"|0000
 +
|align="center"|SS
 +
|align="center"|SSS
 +
|align="center"|SSSS
 +
|}
 +
 
 +
To construct, first fold up the nets for each cube and attach the cubes into the net of a tesseract as shown below, making sure to preserve orientation. Solidify the tesseract net and fold that up too. Then, attach the red, blue, green and yellow pairs of facets to each other in that order, lining up the symbols.
 +
 
 +
<[#embed [hash KV05CMH3C2Q7M8761HHSGX1GM6]]>
 +
 
 +
== See also ==
 +
*[[Paper cutting]]

Latest revision as of 23:23, 11 February 2014

A manifold is a topological object which locally resembles Euclidean space. Manifolds may or may not have boundaries and may or may not be orientable.

Nullar and linear manifolds

The manifolds in 0D and 1D are relatively trivial, but are included for completeness:

nullar linear
Point Line segment Circle
(image) (image) (image)

The colored boundaries (for the circle, the two red points) must be identified to form the desired manifold.

Planar manifolds

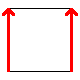
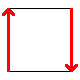
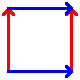
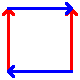
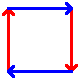
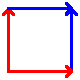
These are the best known manifolds. There are seven "interesting" ones, shown below:

Group 0 Group 1 Group 2
Disc Hose (uncapped cylinder) Möbius strip Torus Klein bottle Real projective plane Sphere
(image) (image) (image) (image) (image) (image) (image)

To construct, connect up the colored edges so that the colors and arrowheads match.

There are infinitely many more such manifolds in group 2, one each of the orientable and non-orientable varieties for each possible genus. Only the possibilities for genus 0 and 1 are shown above.

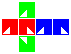
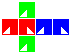
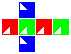
Cubic manifolds

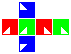
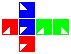
Some examples are shown in the following table.

Group 0-0 Group 1-0 Group 2-0 Group 3-0 Group 0-2 Group 1-2 Group 0-3
Cube Dihose Toric hose Ditorus Spherical hose Glome Torisphere Torispheric bottle
(image) (image) (image) (image) (image) (image) (image) (image)
Möbial hose Real projective planar hose Toric bottle
(image) (image) (image)
Real projective realm
(image)

Construction is similar to that of the square manifolds: fold up each cubic net and attach the red, blue and green pairs of facets to each other in that order, making sure the triangles line up.

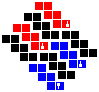
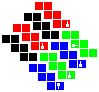
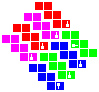
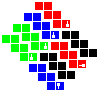
Tesseric manifolds

Here are the 4D p-toric q-hoses and p-spheric q-hoses along with the tesseract and möbial dihose:

Group 0-0 Group 1-0 Group 2-0 Group 3-0 Group 4-0 Group 0-2 Group 0-3 Group 0-4
Tesseract Möbial dihose Trihose Toric dihose Ditoric hose Tritorus Spherical dihose Glomic hose Pentasphere
(image) (image) (image) (image) (image) (image) (image) (image) (image)
I 1 0 00 000 0000 SS SSS SSSS

To construct, first fold up the nets for each cube and attach the cubes into the net of a tesseract as shown below, making sure to preserve orientation. Solidify the tesseract net and fold that up too. Then, attach the red, blue, green and yellow pairs of facets to each other in that order, lining up the symbols.

(image)

See also

Retrieved from "http://hi.gher.space/wiki/Manifold"