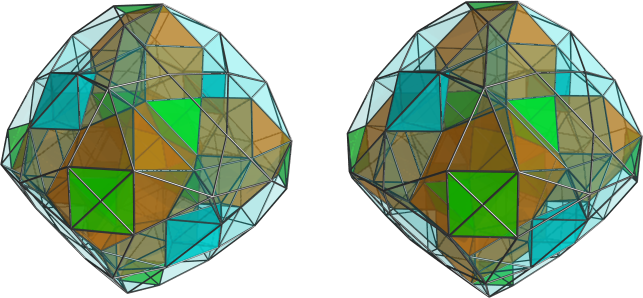D4.10 (EntityTopic, 15)
From Hi.gher. Space
(Add more of Quickfur's comments on the lace tower.) |
m (→Software models: links) |
||
| (3 intermediate revisions not shown) | |||
| Line 2: | Line 2: | ||
{{STS Shape | {{STS Shape | ||
| dim=4 | | dim=4 | ||
| + | | elements=132, 592, 636, 176 | ||
| extra={{STS Polytope | | extra={{STS Polytope | ||
}}}} | }}}} | ||
| - | '''D4.10''' is a [[bilbirothawroid]] with a pair of antipodal tetrahedra surrounded by 6 [[bilunabirotunda]]e (J91) each, with 4 tridiminished icosahedra filling up the gaps between the J91's around each tetrahedron. There are also 8 J92's, 4 on the two identical hemispheres of the polytope, which are oriented in dual orientation to each other. | + | '''D4.10''' is a [[bilbirothawroid]] with a pair of antipodal [[tetrahedra]] surrounded by 6 [[bilunabirotunda]]e (J91) each, with 4 [[tridiminished icosahedra]] filling up the gaps between the J91's around each tetrahedron. There are also 8 [[J92]]'s, 4 on the two identical hemispheres of the polytope, which are oriented in dual orientation to each other. |
It is related to [[D4.11]] via a slight modification of its lace tower. | It is related to [[D4.11]] via a slight modification of its lace tower. | ||
| + | |||
| + | == Elements == | ||
| + | {{TODO|Split faces, edges and vertices into unique positions.}} | ||
| + | ;Cells | ||
| + | *16 [[tetrahedra]] (2 + 6 + 8) | ||
| + | *24 [[square pyramid]]s | ||
| + | *32 [[octahedra]] (24 + 8) | ||
| + | *8 [[tridiminished icosahedra]] | ||
| + | *8 [[triangular cupola]]e | ||
| + | *24 [[pentagonal antiprism]]s | ||
| + | *12 J91's | ||
| + | *8 J92's | ||
| + | |||
| + | ;Faces | ||
| + | *464 [[triangle]]s | ||
| + | *48 [[square]]s | ||
| + | *72 [[pentagon]]s | ||
| + | *8 [[hexagon]]s | ||
| + | |||
| + | *636 edges | ||
| + | *176 vertices | ||
== Lace tower == | == Lace tower == | ||
| Line 69: | Line 91: | ||
</pre></blockquote> | </pre></blockquote> | ||
| - | ==Software models== | + | == Software models == |
| - | + | *[[Polyview]] [http://hddb.teamikaria.com/dl/ZATKWKW47QY9PS9PPSHVWYF7TE.def .def file] | |
| - | * Polyview [http://hddb.teamikaria.com/dl/ZATKWKW47QY9PS9PPSHVWYF7TE.def .def file] | + | *[[Stella4D]] [http://hddb.teamikaria.com/dl/QS746WG1QG36CR3A40JJPQA5RP.off .off file] |
| - | * Stella4D [http://hddb.teamikaria.com/dl/QS746WG1QG36CR3A40JJPQA5RP.off .off file] | + | |
Latest revision as of 21:28, 18 March 2014
D4.10 is a bilbirothawroid with a pair of antipodal tetrahedra surrounded by 6 bilunabirotundae (J91) each, with 4 tridiminished icosahedra filling up the gaps between the J91's around each tetrahedron. There are also 8 J92's, 4 on the two identical hemispheres of the polytope, which are oriented in dual orientation to each other.
It is related to D4.11 via a slight modification of its lace tower.
Elements
TODO: Split faces, edges and vertices into unique positions.
- Cells
- 16 tetrahedra (2 + 6 + 8)
- 24 square pyramids
- 32 octahedra (24 + 8)
- 8 tridiminished icosahedra
- 8 triangular cupolae
- 24 pentagonal antiprisms
- 12 J91's
- 8 J92's
- Faces
- 636 edges
- 176 vertices
Lace tower
x3o3o // tetrahedron
f3o3x // 4 tetrahedra touching vertices of previous one
o3x3f // midpoints of J91's
f3x3x // square faces of J91's
x3o3F // octahedra above J63's
x3F3o // opposite edge of J91's
f3x3f // f3x vertices of 8 J92's (this is the midpoint)
o3F3x
F3o3x
x3x3f
f3x3o
x3o3f
o3o3x
As you can see, there are two antipodal tetrahedra. EDIT 3: Also, there are no lacing edges between f3x3x and x3o3F, so that part of the tower may be better written as:
...
o3x3f
/ f3x3x
x3o3F |
| x3F3o
| f3x3f |
o3F3x |
| F3o3x
x3x3f /
f3x3o
...
Projections
Centered on one of the antipodal tetrahedra:
Same 4D viewpoint, with J92 cells highlighted:
Side-view, showing that it nearly has 16-cell symmetry:
Coordinates
apecs<1/√2, 1/√2, 1/√2> ~ <-(2*phi+3)/√2> apecs<phi^2/√2, phi^2/√2, 1/(phi*√2)> ~ <-(phi+3)/√2> apecs<(phi+2)/√2, phi/√2, -phi/√2> ~ <-(phi+2)/√2> apecs<1/(phi*√2), phi^2/√2, (phi^2+2)/√2> ~ <-phi^2/√2> apecs<-(phi+2)/√2, -phi/√2, -(phi+2)/√2> ~ <-phi/√2> apecs<(2*phi+3)/√2, 1/√2, 1/√2> ~ <-1/√2> apacs<0, phi*√2, phi^2*√2> ~ <0> apecs<1/√2, 1/√2, -(2*phi+3)/√2> ~ <1/√2> apecs<phi/√2, (phi+2)/√2, (phi+2)/√2> ~ <phi/√2> apecs<1/(phi*√2), phi^2/√2, -(phi+3)/√2> ~ <phi^2/√2> apecs<(phi+2)/√2, phi/√2, phi/√2> ~ <(phi+2)/√2> apecs<1/(phi*√2), phi^2/√2, -phi^2/√2> ~ <(phi+3)/√2> apecs<1/√2, 1/√2, -1/√2> ~ <(2*phi+3)/√2>