Geopeton (EntityTopic, 20)
From Hi.gher. Space
(Difference between revisions)
m |
m (K6.4 upgrade: img -> embed) |
||
| (23 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | {{Shape| | + | <[#ontology [kind topic] [cats 6D Hypercube]]> |
| + | {{STS Shape | ||
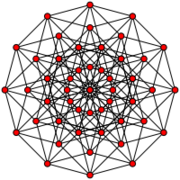
| + | | image=<[#embed [hash 5N7NJKG9P1CPTV2X2D3STA0YSZ] [width 180]]><br>[[Petrie polygon]] | ||
| + | | dim=6 | ||
| + | | elements=12, 60, 160, 240, 192, 64 | ||
| + | | genus=0 | ||
| + | | ssc=[xyzwφσ] | ||
| + | | ssc2=K6c1 | ||
| + | | pv_square=1 | ||
| + | | extra={{STS Tapertope | ||
| + | | order=6, 0 | ||
| + | | notation=111111 | ||
| + | | index=84 | ||
| + | }}{{STS Toratope | ||
| + | | expand=[[Hexeract|111111]] | ||
| + | | notation=IIIIII | ||
| + | | index=21a | ||
| + | }}{{STS Bracketope | ||
| + | | index=194 | ||
| + | }}{{STS Polytope | ||
| + | | altern=[[Demihexeract]] | ||
| + | | dual=[[Aeropeton]] | ||
| + | }}{{STS Uniform polytope | ||
| + | | schlaefli={[[Square|4,]][[Cube|3,]][[Tesseract|3,]][[Pentacube|3,]]3} | ||
| + | | vfigure=[[Pyroteron]], edge √5 | ||
| + | | vlayout=((([[Square|4]][[Cube|<sup>3</sup>]])[[Tesseract|<sup>3</sup>]])[[Pentacube|<sup>3</sup>]])<sup>3</sup> | ||
| + | }}}} | ||
| - | + | The '''geopeton''', also known as the '''hexeract''', the '''hexacube''' and the [[regular]] '''dodecapeton''' is the six-dimensional [[hypercube]]. It is a special case of the [[prism]] where the base is a [[geoteron]]. It is also the [[square]] of the [[cube]]. | |
| - | + | ||
| - | + | == Equations == | |
*Variables: | *Variables: | ||
| - | <blockquote>''l'' ⇒ length of the edges of the | + | <blockquote>''l'' ⇒ length of the edges of the hexeract</blockquote> |
| - | *All points (''x'', ''y'', ''z'', ''w'', ''φ'', ''σ'') that lie on the [[surpeton]] of a | + | *All points (''x'', ''y'', ''z'', ''w'', ''φ'', ''σ'') that lie on the [[surpeton]] of a hexeract will satisfy the following equation: |
<blockquote>''Unknown''</blockquote> | <blockquote>''Unknown''</blockquote> | ||
| - | *The [[hypervolume]]s of a | + | *The [[hypervolume]]s of a hexeract are given by: |
<blockquote>total edge length = 192''l''<br> | <blockquote>total edge length = 192''l''<br> | ||
total surface area = 240''l''<sup>2</sup><br> | total surface area = 240''l''<sup>2</sup><br> | ||
| Line 19: | Line 44: | ||
hexavolume = ''l''<sup>6</sup></blockquote> | hexavolume = ''l''<sup>6</sup></blockquote> | ||
| - | *The [[pentaplanar]] [[cross-section]]s (''n'') of a | + | *The [[pentaplanar]] [[cross-section]]s (''n'') of a hexeract are: |
<blockquote>[!x, !y, !z, !w, !φ, !σ] ⇒ pentacube of side (''l'')</blockquote> | <blockquote>[!x, !y, !z, !w, !φ, !σ] ⇒ pentacube of side (''l'')</blockquote> | ||
| - | + | == Net == | |
| - | The net of a | + | The net of a hexeract is a penteract surrounded by ten more penteracts, with one more penteract added to one of these. |
| + | {{Hypercubes|6}} | ||
{{Hexashapes}} | {{Hexashapes}} | ||
| - | {{ | + | {{Tapertope Nav|83|84|85|21111<br>Penterinder|111111<br>Hexeract|5<sup>1</sup><br>Pentaspheric cone|peta}} |
| - | {{Bracketope Nav|193|194|195|(<xy><(zw)φ>)<br>''Unknown shape''|[xyzwφσ]<br> | + | {{Toratope Nav A|20|21|22|(((II)I)I)I<br>Ditorinder|((((II)I)I)I)<br>Tritorus|IIIIII<br>Hexeract|(IIIIII)<br>Hexasphere|(II)IIII<br>Penterinder|((II)III)<br>Torapenterinder|peta}} |
| - | + | {{Bracketope Nav|193|194|195|(<xy><(zw)φ>)<br>''Unknown shape''|[xyzwφσ]<br>Hexeract|[<xy>zwφσ]<br>Narrow hexeract|peta}} | |
Latest revision as of 20:44, 11 February 2014
The geopeton, also known as the hexeract, the hexacube and the regular dodecapeton is the six-dimensional hypercube. It is a special case of the prism where the base is a geoteron. It is also the square of the cube.
Equations
- Variables:
l ⇒ length of the edges of the hexeract
- All points (x, y, z, w, φ, σ) that lie on the surpeton of a hexeract will satisfy the following equation:
Unknown
- The hypervolumes of a hexeract are given by:
total edge length = 192l
total surface area = 240l2
total surcell volume = 160l3
surteron bulk = 60l4
surpeton pentavolume = 12l5
hexavolume = l6
- The pentaplanar cross-sections (n) of a hexeract are:
[!x, !y, !z, !w, !φ, !σ] ⇒ pentacube of side (l)
Net
The net of a hexeract is a penteract surrounded by ten more penteracts, with one more penteract added to one of these.
| Hypercubes |
| point • digon • square • cube • geochoron • geoteron • geopeton |
| Notable Hexashapes | |
| pyropeton • aeropeton • geopeton • square cubic truncatriate | |
| 83. 21111 Penterinder | 84. 111111 Hexeract | 85. 51 Pentaspheric cone |
| List of tapertopes | ||
| 20a. (((II)I)I)I Ditorinder | 20b. ((((II)I)I)I) Tritorus | 21a. IIIIII Hexeract | 21b. (IIIIII) Hexasphere | 22a. (II)IIII Penterinder | 22b. ((II)III) Torapenterinder |
| List of toratopes | |||||
| 193. (<xy><(zw)φ>) Unknown shape | 194. [xyzwφσ] Hexeract | 195. [<xy>zwφσ] Narrow hexeract |
| List of bracketopes | ||