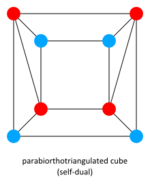
Parabiorthotriangulated cube (EntityTopic, 13)
From Hi.gher. Space
The parabiorthotriangulated cube is one of the non-CRF facets of CRF duals currently being studied by Keiji. It is self-dual, however there is no representation of its incidence matrix such that a rotation of 180° leads directly to the original matrix without an intermediate permutation. As such, the current version of the polytope explorer won't accept it as self-dual, and both forms of the imat are displayed below to illustrate the above phenomenon.
As well as being the first discovered polytope to demonstrate this oversight in the polytope explorer, it is also the first discovered of the non-CRF facets of CRF duals to be self-dual but not chiral.
Incidence matrix
Dual: parabiorthotriangulated cube_
| # | TXID | Va | Vb | Ea | Eb | Ec | Ed | 4a | 3a | Type | Name |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Va | = point | ; red | ||||||||
| 1 | Vb | = point | ; blue | ||||||||
| 2 | Ea | 2 | 0 | = digon | ; lateral | ||||||
| 3 | Eb | 2 | 0 | = digon | ; frontal | ||||||
| 4 | Ec | 1 | 1 | = digon | ; diagonal | ||||||
| 5 | Ed | 0 | 2 | = digon | ; end | ||||||
| 6 | 4a | 2 | 2 | 1 | 0 | 2 | 1 | = square | ; | ||
| 7 | 3a | 2 | 1 | 0 | 1 | 2 | 0 | = triangle | ; | ||
| 8 | C1a | 4 | 4 | 2 | 2 | 8 | 2 | 4 | 4 | = parabiorthotriangulated cube | ; |
Usage as facets
- 12× 1-facets of a (dual of triangular hebesphenorotundaeic rhombochoron)
Incidence matrix
Dual: parabiorthotriangulated cube
| # | TXID | Va | Vb | Ea | Eb | Ec | Ed | 3a | 4a | Type | Name |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Va | = point | ; | ||||||||
| 1 | Vb | = point | ; | ||||||||
| 2 | Ea | 0 | 2 | = digon | ; | ||||||
| 3 | Eb | 1 | 1 | = digon | ; | ||||||
| 4 | Ec | 2 | 0 | = digon | ; | ||||||
| 5 | Ed | 0 | 2 | = digon | ; | ||||||
| 6 | 3a | 1 | 2 | 1 | 2 | 0 | 0 | = triangle | ; | ||
| 7 | 4a | 2 | 2 | 0 | 2 | 1 | 1 | = square | ; | ||
| 8 | C1a | 4 | 4 | 2 | 8 | 2 | 2 | 4 | 4 | = parabiorthotriangulated cube_ | ; |
Usage as facets
This polytope does not currently appear as facets in any higher-dimensional polytopes in the database.