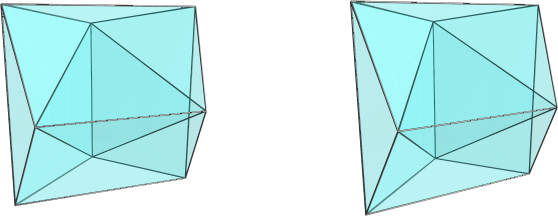
Digonal gyrobicupolic ring (EntityTopic, 17)
From Hi.gher. Space
The digonal gyrobicupolic ring, or K4.8, is a member of the set of bicupolic rings. Its cells are 1 tetrahedron, 4 square pyramids and 2 triangular prisms. Its faces are 1+4 squares and 4+4+4 triangles. It has 2+4+4+8 edges and 4+4 vertices.
Keiji studied it explicitly to try to understand more about the segmentochora.
Construction
It is possible to construct the digonal gyrobicupolic ring from three different pairs of polytopes:
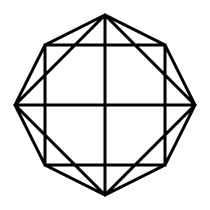 Petrie polygon |  Square pyramid and opposite triangle highlighted | 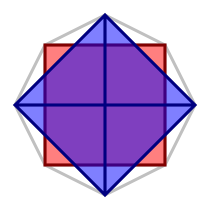 Tetrahedron and opposite square highlighted |  Triangular prism and opposite digon highlighted |
This segmentochoron also arises from a bidiminishing of the pyrorectichoron. First, delete any vertex from the pyrorectichoron. That forms the (mono)diminished pyrorectichoron, better known as the trigonal biantiprismatic ring, or K4.6; its cells are 1 triangular prism, 2 octahedra, 3 square pyramids, and 3 tetrahedra. It can be constructed as trigonal prism || gyrated triangle; if a vertex from the gyrated triangle is deleted, it will create a second triangular prism, thus resulting in this segmentochoron.
Projections
The following projection shows this segmentochoron from a viewpoint analogous to that of the other bicupolic rings, to show how the gyrated digons connect to each other via a tetrahedron (digon antiprism) and to the opposite square face via triangular prisms (digon cupolae).
Software models
Incidence matrix
Dual: K4.8 dual
| # | TXID | Va | Vb | Ea | Eb | Ec | Ed | 3a | 3b | 3c | 4a | 4b | C1a | C2a | C3a | Type | Name |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Va | = point | ; | ||||||||||||||
| 1 | Vb | = point | ; | ||||||||||||||
| 2 | Ea | 2 | 0 | = digon | ; | ||||||||||||
| 3 | Eb | 1 | 1 | = digon | ; | ||||||||||||
| 4 | Ec | 0 | 2 | = digon | ; | ||||||||||||
| 5 | Ed | 0 | 2 | = digon | ; | ||||||||||||
| 6 | 3a | 2 | 1 | 1 | 2 | 0 | 0 | = triangle | ; | ||||||||
| 7 | 3b | 1 | 2 | 0 | 2 | 1 | 0 | = triangle | ; | ||||||||
| 8 | 3c | 0 | 3 | 0 | 0 | 2 | 1 | = triangle | ; | ||||||||
| 9 | 4a | 4 | 0 | 0 | 0 | 4 | 0 | = square | ; | ||||||||
| 10 | 4b | 2 | 2 | 1 | 2 | 0 | 1 | = square | ; | ||||||||
| 11 | C1a | 4 | 2 | 4 | 4 | 0 | 1 | 2 | 0 | 0 | 1 | 2 | = triangular prism | ; | |||
| 12 | C2a | 2 | 3 | 1 | 4 | 2 | 1 | 1 | 2 | 1 | 0 | 1 | = square pyramid | ; | |||
| 13 | C3a | 0 | 4 | 0 | 0 | 4 | 2 | 0 | 0 | 4 | 0 | 0 | = tetrahedron | ; | |||
| 14 | H4.1a | 4 | 4 | 4 | 8 | 4 | 2 | 4 | 4 | 4 | 1 | 4 | 2 | 4 | 1 | = K4.8 | ; |
Usage as facets
This polytope does not currently appear as facets in any higher-dimensional polytopes in the database.