CRFP4DP/Diminishings (Meta, 14)
From Hi.gher. Space
Some diminishings of uniform polychora produce various segmentotopes.
- The monodiminished rectified 5-cell is trigon||gyrated triangular prism (K4.6.2).
- The bidiminished rectified 5-cell is line||orthogonal triangular prism (K4.8.2).
- Deleting the vertices of an octahedron from the cantellated 5-cell produces cuboctahedron||truncated_tetrahedron (K4.48).
- The rectified tesseract can be cut into three segmentochora: tetrahedron||truncated_tetrahedron, truncated_tetrahedron||truncated_dual_tetrahedron, and dual_truncated_tetrahedron||dual_tetrahedron.
- The runcinated tesseract can be cut into two cube||rhombicuboctahedron and one rhombicuboctahedron prism. The former in turn can be cut into two square orthobicupolic rings and a square cupola prism, and the latter can be cut into two square cupola prisms and a 4,8-duoprism (octagonal prism prism).
- The cantellated tesseract can be cut into rhombicuboctahedron||truncated_cube and a truncated cube prism.
- The bisected 24-cell (see below) is the segmentochoron octahedron||cuboctahedron; it can be further diminished into square_pyramid||cuboctahedron (K4.31) and subsequently square||cuboctahedron (K4.28).
Parabidiminished xylorectichoron (see section below on diminishings of uniform polychora)
Birotundular ring
Diminishing the 600-cell wedge #4 produces an analogue of the bicupolic rings: the pentagonal gyrobirotundular ring (see the section on 600-cell bisections below). This CRF is bistratic, as its vertices can be placed on 3 parallel hyperplanes.
Tristratic polychora
On February 13, 2014 a new crown jewel was discovered by student91.[1] It is the 5th 4D crown jewel found, and can be written as oxFx3xfox5xoxx&#xt, making it tristratic. It has 70 tets + 20 J92's + 13 ids + 12 pecues + 60 squippies + 30 trips + 1 grid. The tentative name is triacontaspheno-rectified 120-cell rotunda, or triacontasphenorotunda for short. It has many analogous characteristics to the J92 itself, and also has a CRF diminishing.
Quadrastratic polychora
On February 4, 2014 the castellated rhodoperihedral prism was discovered by quickfur and confirmed by Klitzing.[2] This is a crown jewel CRF polychoron - the third to be found, after the snubdis antiprism and the ursachora. It is quadrastratic because its vertices can be placed on five parallel realms, and it can be written as xFoFx3ooooo5xofox&#xt = srid || pseudo F-ike || pseudo f-doe || pseudo F-ike || srid where F = ff = x+f, i.e. φ2≈2.618x.
It also has a Stott-expanded variant, the castellated rhodopantohedral prism, which was first suggested by student91 and consists of two parallel rhodopantohedra, 30 bilunabirotundae, 40 triangular prisms, 24 pentagonal cupolae, and 72 pentagonal prisms.
Convex non-uniform scaliform
Outside the uniform polychora (uniformed-celled and vertex transitive), there are three known convex scaliform (equilateral and vertex transitive) polytopes. All their ridges are regular.
- Bixylodiminished hydrochoron (aka bi-icositetradiminished 600-cell)
- The 600-cell can be made as the convex hull of five 24-cells. Removing the vertices of one and taking the convex hull creates the snub 24-cell. Removing another and taking the convex hull creates this shape. It cells are 48 tridimished icosahedra.
- Prismatorhombato snub 24-cell
- This is made by shrinking the 24 icosahedral cells of a snub 24-cell (all the tetrahedra are removed). Where icosahedra used to be joined by triangles they are now separated by triangular prisms (96 in total). The holes in the shape are filled with 24 truncated tetrahedra and 96 triangular cupola.
- Swirlprismatodiminished rectified 600-cell
- The Rectified 600-cell can be made as the convex hull of 6 600-cells. Removing the vertices of one and taking the convex hull of the remaining vertices produces this shape. Its cells are 600 square pyramids, 120 pentagonal prisms and 120 pentagonal antiprisms.
Diminished polychora
Some regular polychora can be diminished to give CRF polychora.
Pyromorphs
Some of the 5-cell family polychora can be diminished to give various segmentochora (included in Klitzing's list). Some diminishings are not monostratic, however:
- The cantellated 5-cell can have two triangles deleted from it in such a way that it produces a polychoron with 2 hexagonal prisms, 4 square pyramids, 1 cuboctahedron, 4 triangular cupola, and 4 triangular prisms. This produces the bitrigonal diminished pyrocantichoron.

- The runcitruncated 5-cell can have the vertices of a truncated tetrahedron deleted, producing a polychoron with 4 triangular cupola, 1 cuboctahedron, 6 hexagonal prisms, 4 triangular prisms, and 4 truncated tetrahedra.
Stauromorphs
- The diminished 16-cell coincides with the octahedral pyramid (see Prismatoid forms above).
- The rectified tesseract can have the vertices of two non-antipodal, non-touching tetrahedra deleted, producing a polychoron with 2 truncated tetrahedra, 6 triangular cupola, 6 tetrahedra, and 1 cubocatahedron. (Metabidiminished rectified tesseract.) (Note that cutting off one tetrahedron or two antipodal tetrahedra produces various stacked segmentochora.)
- The cantellated tesseract can have square magnabicupolic rings cut off from it to produce CRFs. Each candidate square magnabicupolic ring corresponds with one of the 24 ridges of a tesseract, and two cuttings are only allowed if these ridges do not share an edge. Thus, it corresponds with the number of non-adjacent vertices of the 24-cell; there are 19 such diminishings (see 24-cell diminishings). The octadiminished cantellated tesseract coincides with the 8,8-duoprism; many of the other diminishings correspond with augmentations of the 8,8-duoprism. Five of these diminishings do not correspond with any augmented 8,8-duoprism, because the bicupolic rings are cut off in a 'skewed' way that breaks duoprism symmetry.
- The runcitruncated 16-cell can be diminished to form a rotunda (see below).
Xylomorphs
Xylochoron
The 24-cell can have non-adjacent vertices deleted to form various CRF polychora (this is equivalent to cutting off cubical pyramids). There are 19 such diminishings, one of which is the tesseract. 13 of these coincide with augmentations of the tesseract with cubical pyramids.
- Diminished 24-cell
- Orthobidiminished 24-cell (ortho means two deleted vertices lie on antipodes of one octahedral cell)
- Metabidiminished 24-cell (meta means two deleted vertices are separated by an additional edge past the antipodes of octahedral cells containing one of them)
- Parabidiminished 24-cell (para means two deleted vertices are 24-cell antipodes)
- Orthotridiminished 24-cell (all 3 vertices ortho to each other)
- Paratridiminished 24-cell (two vertices are para to each other, ortho to the third)
- Metatridiminished 24-cell (two vertices are meta, third is ortho to both)
- Orthotetradiminished 24-cell (all 4 vertices ortho to each other)
- Paratetradiminished 24-cell (one pair of vertices para to each other, ortho to other two)
- Orthometatetradiminished 24-cell (3 vertices ortho to each other, last vertex meta to one of them)
- Cyclotetradiminished 24-cell (4 vertices lie on a great circle)
- Metametatetradiminished 24-cell (two pairs of ortho vertices, meta to each other)
- Orthopentadiminished 24-cell (1 pair of para vertices, ortho to all others)
- Metapentadiminished 24-cell (4 vertices ortho to each other, 5th vertex meta to all of them)
- Parapentadiminished 24-cell (2 pairs of para vertices, all ortho to 5th)
- Orthohexadiminished 24-cell (2 pairs of para vertices, ortho to each other & everything else)
- Parahexadiminished 24-cell (3 pairs of para vertices)
- Heptadiminished 24-cell (augmented tesseract)
- (Octadiminished 24-cell == tesseract)
The tesseract augmentations are precisely those that are only ortho or para; all meta-diminishings are not augmented tesseracts; there are 6 of these.
The maximally-diminished 24-cells (those from which no more vertices can be deleted without becoming non-CRF) are the metametatetradiminished 24-cell, the metapentadiminished 24-cell, and the tesseract.
Furthermore, the 24-cell can be bisected to form a segmentochoron octahedron||cuboctahedron, which can be further diminished by deleting up to two more cubical pyramids. All three are segmentochora in Klitzing's list (see segmentotopes section above). Thus, there are 21 diminishings of the 24-cell altogether (not counting the tesseract). Among these, 18 are new CRFs not included in previous categories.
The 24-cell diminishings have been independently enumerated by wintersolstice, Marek, and quickfur.
Xylorectichoron
- Parabidiminished xylorectichoron: deleting the vertices of two antipodal cuboctahedra from the xylorectichoron (o3x4o3o) produces a CRF polychoron having two truncated octahedra, 6 cuboctahedra, 12 cubes, and 16 triangular cupolae:
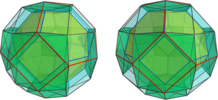
- Metabidiminished xylorectichoron: deleting the vertices of two non-antipodal cuboctahedra that are meta to each other produces a different CRF polychoron with two touching truncated octahedra (TBD: enumerate other cells)
- Metatridiminished xylorectichoron: deleting the vertices of three cuboctahedra meta to each other produces a CRF polychoron with 3 truncated octahedra, 6 cubes, and 18 triangular cupolae.

Snub demitesseract
The snub demitesseract has a CRF vertex figure, which gives rise to several CRF derivations:
- the truncated snub demitesseract, consisting of 24 truncated icosahedra, 96 tridiminished icosahedra, and 120 truncated tetrahedra;
- the rectified snub demitesseract;
- the runcinated snub demitesseract (aka prismatorhombato snub 24-cell), which is scaliform.
Rhodomorphs
Diminished 600-cells
The 600-cell has a large number of diminishings, two of which are uniform (the snub 24-cell and the grand antiprism). Removing icosahedral pyramids from the 600-cell generates a large number of CRF polychora; removing 24 in 24-cell configuration generates the snub 24-cell. Removing two rings of 10 vertices each from mutually complementary 2-planes generates the grand antiprism; removing subsets of these vertices generates various intermediates (full exploration of the possibilities still in progress).
Mathieu Sikirić and Wendy Myrvold proved in their 2007 paper The special cuts of the 600-cell that there are 314,248,344 non-adjacent diminishings of the 600-cell (up to isomorphism). A far larger number of CRFs are produced if some adjacent diminishings are included. The exact figure is currently unknown.
Bisected 600-cells
The 600-cell can be "bisected" by removing all vertices that lie on one side of an inscribed icosidodecahedron. (This is not a true bisection, as 12 edges that are bisected by the cutting hyperplane are completely removed from the result, instead of producing half-length edges, which would make the result non-CRF.) The result is a polychoron with 270 tetrahedra, 12 pentagonal pyramids, and 1 icosidodecahedron. It may be called a "hemi-600-cell". Various other diminishings past this point are possible, including Wendy's tristratic point||icosahedron||dodecahedron||icosidodecahedron (rendered here), which is obtained by deleting the vertices of an inscribed icosahedron (larger than the edge length) from the bisected 600-cell; and a bistratic CRF having 1 icosahedron, 20 tridiminished icosahedra, 12 pentagonal pyramids, and 1 icosidodecahedron (see bistratics section above).
The hemi-600-cell can be further bisected by choosing the cutting hyperplane in such a way that it neatly bisects the bottom icosidodecahedron. Bisected edges are discarded and replaced with pentagonal pyramids to keep the result CRF. There are 4 such cuttings known, which result in wedges of various dichoral angles between the two resulting pentagonal rotundae:
- Wedge #1: 2 pentagonal rotundae, 12 pentagonal pyramids, and 210 tetrahedra. This is the widest wedge, with dichoral angle of 144° between the rotundae:
- Wedge #2: 2 pentagonal rotundae, 12 pentagonal pyramids, and 150 tetrahedra. A slightly narrower wedge, with dichoral angle of 108° between the rotundae:
- Wedge #3: 2 pentagonal rotundae, 12 pentagonal pyramids, and 90 tetrahedra. An even narrower wedge, with dichoral angle of 72° between rotundae:
- Wedge #4: 2 pentagonal rotundae, 12 pentagonal pyramids, and 30 tetrahedra. The narrowest wedge, with dichoral angle of 36° between rotundae (top view this time, instead of side view):
All of these wedges can be further diminished by deleting various vertices. Removing the vertex antipodal to the decagonal face in wedge #4 produces a rotunda analogue of the gyrobicupolic rings: the pentagonal gyrobirotundular ring, having 1 pentagonal antiprism flanked by a ring of 20 tetrahedra, which in turn are flanked by a ring of 10 pentagonal pyramids, with two pentagonal rotundae closing up the shape.
Rotundae
So far, seven CRF rotundae have been discovered, all of which can be derived by diminishing uniform polychora. The vertices of these shapes lie in more than 2 parallel hyperplanes, therefore they are not included among Klitzing's segmentochora.
|
No image |
These rotundae have birotunda forms as well as their corresponding elongates. Two of these, the octahedral birotunda and the elongated stauroperihedral birotunda, are uniform (truncated 16-cell and runcitruncated 16-cell, respectively), so there are 28-2=26 new CRF polychora in total.