D4.15 (EntityTopic, 13)
From Hi.gher. Space
Most of the content on this page is taken directly from the forum thread where it was discovered.
The magnaursachoron is a CRF polytope discovered by User:Quickfur in March 2016. It can be thought of as a 4D analogue of the tridiminished rhodoperihedron, or J83, in a similar way to how the pyroursachoron is a 4D analogue of teddi.
It consists of a cuboctahedron as the top cell, surrounded by 4 J83's in tetrahedral symmetry, with triangular prisms and tridiminished icosahedra filling in the gaps between them. The bottom of the shape is closed up with more tridiminished icosahedra, cuboctahedra, triangular prisms, metabidiminished icosahedra, triangular cupolae, and capped off with a truncated tetrahedron at the bottom.
The full symbol of this CRF polychoron is:
xxFVF(Vx)fox-3-ofxxf(oF)xxx-3-xoooo(xo)xfo-&#xt
(with V=2f, that is, twice the Golden Ratio).
Cell counts
- 1+4 = 5 x3o3x
- 6+4+12+12 = 34 triangular prisms
- 4+4 = 8 J63's (teddies)
- 4 J83's (tetrids)
- 6 J62's (mibdies)
- 4 triangular cupolae
- 1 truncated tetrahedron
- Total: 62 cells.
Coordinates
The coordinates are:
apacs<0, √2, √2> ~ <-3*φ²/√2> apecs<1/√2, 1/√2, (1+2*φ)/√2> ~ <-(3*φ+2)/√2> apecs<φ²/√2, φ²/√2, (φ+3)/√2> ~ <-2*φ²/√2> apecs<φ*√2, φ*√2, φ²*√2> ~ <-φ²/√2> apecs<φ²/√2, φ²/√2, (1+3*φ)/√2> ~ <0> apecs< 1/√2, 1/√2, (3+2*φ)/√2> ~ <φ/√2> apecs<(2*φ-1)/√2, (2*φ+1)/√2, (2*φ+1)/√2> ~ <φ/√2> apecs<1/(φ*√2), φ²/√2, (φ+3)/√2> ~ <2*φ/√2> apecs<-φ/√2, φ/√2, (φ+2)/√2> ~ <(2*φ+1)/√2> apecs<1/√2, 1/√2, 3/√2> ~ <3*φ/√2>
where φ=(1+√5)/2 is the Golden Ratio, apacs means "all permutations and changes of sign", apecs means "all permutations and even changes of sign", and ~ means vector concatenation (this notation is mainly to concisely express vertex layers in terms of apacs and apecs while assigning the height of the layer separately).
Lace tower
there may be mistakes, in several of the layers the coordinates were obtained by "completing the pentagons/decagons" rather than straight from the CD symbol, so the symbols may be wrong
x3o3x (top cuboctahedron)
x3f3o (top half of (upside-down) teddies)
F3x3o (end of teddies)
V3x3o (V=f+f, I think. This is half of the decagons)
F3f3o (not 100% sure about the f, this is 2nd last set of vertices of decagons)
/ \
x3B3o C3o3f (not sure what B and C are, this is last vertices of decagon and 2nd set of teddies)
\ /
f3x3D (2nd last layer of vertices of tetrids, not sure what D is)
o3x3f (last vertices of tetrids)
x3x3o (bottom cell, it turns out to be a truncated tetrahedron!)
Images
Here's the top view, looking at the x3o3x:
Here, you can see the triangular prisms around the x3o3x interfacing with the upside-down teddies and the tetrids. The tetrids appear quite flat from this viewpoint because they are quite slanted into the 4th direction. You can see the outlines of the 2nd layer of teddies at the corners of the tetrahedroid shape of the projection, around the outer triangular prisms (they are on the far side of the polychoron from this viewpoint).
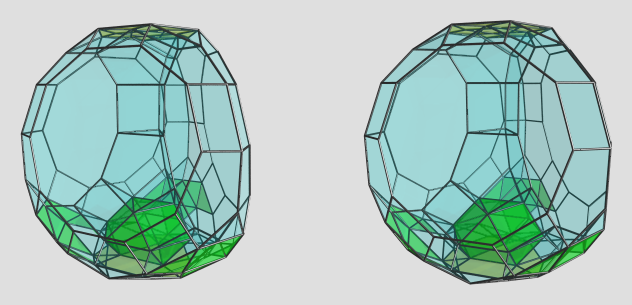
The most interesting part of this polychoron is the bottom. It turns out that it can be closed with just another layer of vertices beyond the tetrids, as indicated by the lace tower; among the cells that fill in the gaps are metabidiminished icosahedra and more cuboctahedra, along with triangular cupolae.
The green cells are cuboctahedra linking the bottom cell to the 2nd layer of teddies. Between each pair of cuboctahedra are metadiminished icosahedra, serving as wedges that sit between the gaps between the bottom part of the tetrids, more triangular prisms, and triangular cupolae linking the bottom cell to the bottom triangles of the tetrids.
So far, we haven't had a good view of the tetrids, so let's take a side view next:
Here, we're looking at how 3 tetrids fold together around a column of teddies and triangular prisms. Below the 2nd layer of teddies we have cuboctahedra linking to the bottom cell.