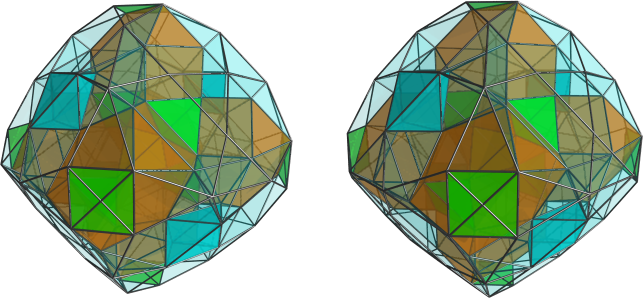D4.10 (EntityTopic, 15)
From Hi.gher. Space
D4.10 is a bilbirothawroid with a pair of antipodal tetrahedra surrounded by 6 bilunabirotundae (J91) each, with 4 tridiminished icosahedra filling up the gaps between the J91's around each tetrahedron. There are also 8 J92's, 4 on the two identical hemispheres of the polytope, which are oriented in dual orientation to each other.
Projections
Centered on one of the antipodal tetrahedra:
Same 4D viewpoint, with J92 cells highlighted:
Side-view, showing that it nearly has 16-cell symmetry:
Coordinates
apecs<1/√2, 1/√2, 1/√2> ~ <-(2*phi+3)/√2> apecs<phi^2/√2, phi^2/√2, 1/(phi*√2)> ~ <-(phi+3)/√2> apecs<(phi+2)/√2, phi/√2, -phi/√2> ~ <-(phi+2)/√2> apecs<1/(phi*√2), phi^2/√2, (phi^2+2)/√2> ~ <-phi^2/√2> apecs<-(phi+2)/√2, -phi/√2, -(phi+2)/√2> ~ <-phi/√2> apecs<(2*phi+3)/√2, 1/√2, 1/√2> ~ <-1/√2> apacs<0, phi*√2, phi^2*√2> ~ <0> apecs<1/√2, 1/√2, -(2*phi+3)/√2> ~ <1/√2> apecs<phi/√2, (phi+2)/√2, (phi+2)/√2> ~ <phi/√2> apecs<1/(phi*√2), phi^2/√2, -(phi+3)/√2> ~ <phi^2/√2> apecs<(phi+2)/√2, phi/√2, phi/√2> ~ <(phi+2)/√2> apecs<1/(phi*√2), phi^2/√2, -phi^2/√2> ~ <(phi+3)/√2> apecs<1/√2, 1/√2, -1/√2> ~ <(2*phi+3)/√2>