
Johnsonian Polytopes
Re: Johnsonian Polytopes
Haha you're right!! It's just the x4o3x3o all over again. 

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Okay, your expansion idea does not produce something really new in the case of quawros.
So lets look, what it would produce in case of stawros then.
And here would be its lace city display:
This is not wrong at all. It is just a Grünbaumian structure with completely coincident elements. In fact this is what occurs as truncated pentagram in general: x5/2o becomes x5/2x, i.e. a sequence of ten lines twirling around the center 2 times: This is nothing but a pentagon which would be outlined twice!
But we could get rid of this anomaly. Just omit both coincident elements and close the then open pairs of coincident ridges. Applied here this would make all these pips virtual. Their subelements would stay in place, cross-connecting then the former incident elements.
Thus we end with a final shape, still being displayed by the very same lace city (just being interpreted a bit different), having for facets: 10 stips + 50 trips + 25 tets + 25 cubes. - Obviously regular faced, but again using pentagrams (here not only in arrangement, but even as faces. Thus this figure too would not be convex.
--- rk
So lets look, what it would produce in case of stawros then.
- So we would have to start with the 5/2,10-dip ("stardedip"). This figure has 10 stips + 5 dips.
- Next we augment each dip with pip||dip, each having a consist of 1 pip + 5 trips + 5 cubes + 1 dip + 2 pecues.
(Thus in total we have for this complex so far: 10 stips + 5 pips + 25 trips + 25 cubes + 10 pecues.) - Finally we bridge each gap between those pecues by pip||{10}, each having for facets 1 pip + 5 trips + 5 tets + 2 pecues.
(So we are left in the end with: 10 stips + 10 pips + 50 trips + 25 cubes + 25 tets.)
And here would be its lace city display:
- Code: Select all
x5o x5o
x5x
x5x x5x
x5o x5o
x5x x5x
x5o
This is not wrong at all. It is just a Grünbaumian structure with completely coincident elements. In fact this is what occurs as truncated pentagram in general: x5/2o becomes x5/2x, i.e. a sequence of ten lines twirling around the center 2 times: This is nothing but a pentagon which would be outlined twice!
But we could get rid of this anomaly. Just omit both coincident elements and close the then open pairs of coincident ridges. Applied here this would make all these pips virtual. Their subelements would stay in place, cross-connecting then the former incident elements.
Thus we end with a final shape, still being displayed by the very same lace city (just being interpreted a bit different), having for facets: 10 stips + 50 trips + 25 tets + 25 cubes. - Obviously regular faced, but again using pentagrams (here not only in arrangement, but even as faces. Thus this figure too would not be convex.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
quickfur wrote:[...] The following CRF was described by wintersolstice as a gyrated version of the cube cupola:
Basically, take a cube cupola, cut off a square orthobicupolic ring, and replace it with a square gyrobicupolic ring. [...]
Note that this CRF is not in Klitzing's list, because its vertices lie on more than two parallel hyperplanes.
That post of quickfur indeed is not a segmentochoron. But it can be considered a tristratic stack (as external blend) of those:
- Code: Select all
[x4o||(x4o||x4x)] + [(x4o||x4x)||(x4o||x4x)] + [(x4o||x4x)||o4x],
i.e.: K-4.73 + K-4.69 + K-4.64
Note that K-4.69 and K-4.73 both have radius sqrt((3+sqrt(2))/2) and indeed can be added into a common hypersphere. In fact, they assemble as K-4.72 (cube||escu). Note further that the height of K-4.73 is 1/sqrt(2) = 0.707107, while that of K-4.64 is sqrt((sqrt(8)-1)/4) = 0.676097. Therefore that final square indeed misses to be at the hypersphere running through all other vertices.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
In the subsequent mail quickfur then writes:
Gyration (in its usual understanding) cuts off some cap (just like a diminishing) and then puts it back "the wrong way". I.e. The gyrated element is re-used itself.
OTOH, your figure is rather an augmented diminishing. As it uses a different cap which is attached onto the diminished version.
--- rk
This is wrong however.which I will tentatively name the gyro cube cupola
Gyration (in its usual understanding) cuts off some cap (just like a diminishing) and then puts it back "the wrong way". I.e. The gyrated element is re-used itself.
OTOH, your figure is rather an augmented diminishing. As it uses a different cap which is attached onto the diminished version.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
Yes I do, even so since that post of yours there have been 5 1/2 months...quickfur wrote:Does anybody still read this thread?
Your count is wrong, so. There are 4 tricues. - This would even be clearly obvious: the hips do connect at a square, not at a hexagon. Therefore there would be 4 hexagons to connect to. Accordingly there are 4 tricues needed.Well, I hope somebody's reading, 'cos I've discovered a new non-trivial CRF! Here is a projection of it:
(This is a cross-eyed stereo pair; see here if you're new to cross-eyed stereo viewing.)
Its cells are 1 cuboctahedron, 2 hexagonal prisms, 2 triangular cupolae, 4 square pyramids, 4 triangular prisms.
[...] I discovered this CRF while searching for maximally-diminished uniform polychora (defined to be a CRF polychoron obtained by some diminishing of a uniform polychoron, such that no more vertices can be removed from it without making it non-CRF). The cantellated 5-cell can have 3 vertices on one triangular face removed from it, producing a CRF with 1 hexagonal prism, 2 triangular cupola, 2 octahedra, 3 cuboctahedra, 7 triangular prisms, and 3 square pyramids. That polychoron I tentatively call the "triangle-diminished cantellated 5-cell"; the hexagonal prism is opposite a triangular prism. Another triangle of vertices can be removed from it, to produce the polychoron shown above. This triangle has 1 vertex touching the apex of a square pyramid and shares an edge with the triangular prism opposite the hexagonal prism. (It's important exactly which triangle to remove, since removing the wrong one produces a non-CRF polychoron.)
I think the result is maximally-diminished, but I'm not 100% sure. (Another maximal diminishing of the cantellated 5-cell is the bisected cantellated 5-cell, which is the same as the segmentochoron cuboctahedron||truncated_tetrahedron (4.48 in Klitzing's list).)
Anybody up for naming this little pretty? I'm thinking bi-triangle-diminished cantellated 5-cell, but I don't like the name; it sounds ugly. Any suggestions?
Well, that name is completely correct in its description. I have no other one at hand. You just might substitute "cantellated 5-cell" by "srip" and further could make the "triangle" implicite (by context), getting "bi-diminished srip".
Now to the figure itself.
You probably know that srip could be given as a bistratic stack "oct||tut||co". Each diminishing chops off a triangle being built from one oct-vertex and one edge of tut (which connects 2 hexagons). If both are applied here, the top oct gets reduced to nothing, just its equatorial square will be left. From that tut only an obtuse hexahedron would be left, having 2 faces being 2:1-rectangles and 4 faces being 1:1:1:2-trapeziums. At the opposite co those diminishings would scratch only at a pair of opposite squares. So it remains in place, unchanged.
The stereo pair display is quite helpful, if one can visualize that. Perhaps you might like to do a further rendering, which displays that "{4}||...||co" a bit better? (Most probably this would be best achieved by a co-first view.) You even might highlight the 2 hips by an transparent color. Or rather the 4 squippies?
For those which are not so good in viewing stereo pairs, I'd like to add its incidence matrix here below:
- Code: Select all
4 * * * | 2 2 0 0 0 0 0 0 0 0 | 1 2 2 1 0 0 0 0 0 0 0 0 | 2 2 0 0 0 hip-hip square ones
* 8 * * | 0 1 1 1 1 1 0 0 0 0 | 0 1 1 1 1 2 1 1 0 0 0 0 | 1 2 1 1 0 intermediates
* * 8 * | 0 0 0 0 1 0 1 1 1 1 | 0 0 1 0 1 1 0 1 1 1 1 1 | 1 1 1 1 1 polar ones of co
* * * 4 | 0 0 0 0 0 2 0 0 2 2 | 0 0 0 0 0 2 1 2 0 2 1 1 | 0 1 2 1 1 medial ones of co
--------+---------------------+-------------------------+----------
2 0 0 0 | 4 * * * * * * * * * | 1 1 1 0 0 0 0 0 0 0 0 0 | 2 1 0 0 0
1 1 0 0 | * 8 * * * * * * * * | 0 1 1 1 0 0 0 0 0 0 0 0 | 1 2 0 0 0
0 2 0 0 | * * 4 * * * * * * * | 0 1 0 0 1 0 1 0 0 0 0 0 | 1 1 0 1 0 hip-lacing
0 2 0 0 | * * * 4 * * * * * * | 0 0 0 1 0 2 0 0 0 0 0 0 | 0 2 1 0 0 wedge-edges
0 1 1 0 | * * * * 8 * * * * * | 0 0 1 0 1 1 0 1 0 0 0 0 | 1 1 1 1 0
0 1 0 1 | * * * * * 8 * * * * | 0 0 0 0 0 1 1 1 0 0 0 0 | 0 1 1 1 0
0 0 2 0 | * * * * * * 4 * * * | 0 0 1 0 0 0 0 0 1 0 1 0 | 1 1 0 0 1 hip-base
0 0 2 0 | * * * * * * * 4 * * | 0 0 0 0 1 0 0 0 1 0 0 1 | 1 0 0 1 1 hip-lacing
0 0 1 1 | * * * * * * * * 8 * | 0 0 0 0 0 1 0 0 0 1 1 0 | 0 1 1 0 1 tricu-lacing
0 0 1 1 | * * * * * * * * * 8 | 0 0 0 0 0 0 0 1 0 1 0 1 | 0 0 1 1 1 squippy-lacing
--------+---------------------+-------------------------+----------
4 0 0 0 | 4 0 0 0 0 0 0 0 0 0 | 1 * * * * * * * * * * * | 2 0 0 0 0
2 2 0 0 | 1 2 1 0 0 0 0 0 0 0 | * 4 * * * * * * * * * * | 1 1 0 0 0
2 2 2 0 | 1 2 0 0 2 0 1 0 0 0 | * * 4 * * * * * * * * * | 1 1 0 0 0
1 2 0 0 | 0 2 0 1 0 0 0 0 0 0 | * * * 4 * * * * * * * * | 0 2 0 0 0
0 2 2 0 | 0 0 1 0 2 0 0 1 0 0 | * * * * 4 * * * * * * * | 1 0 0 1 0
0 2 1 1 | 0 0 0 1 1 1 0 0 1 0 | * * * * * 8 * * * * * * | 0 1 1 0 0
0 2 0 1 | 0 0 1 0 0 2 0 0 0 0 | * * * * * * 4 * * * * * | 0 1 0 1 0
0 1 1 1 | 0 0 0 0 1 1 0 0 0 1 | * * * * * * * 8 * * * * | 0 0 1 1 0
0 0 4 0 | 0 0 0 0 0 0 2 2 0 0 | * * * * * * * * 2 * * * | 1 0 0 0 1
0 0 2 2 | 0 0 0 0 0 0 0 0 2 2 | * * * * * * * * * 4 * * | 0 0 1 0 1
0 0 2 1 | 0 0 0 0 0 0 1 0 2 0 | * * * * * * * * * * 4 * | 0 1 0 0 1
0 0 2 1 | 0 0 0 0 0 0 0 1 0 2 | * * * * * * * * * * * 4 | 0 0 0 1 1
--------+---------------------+-------------------------+----------
4 4 4 0 | 4 4 2 0 4 0 2 2 0 0 | 1 2 2 0 2 0 0 0 1 0 0 0 | 2 * * * * hip
2 4 2 1 | 1 4 1 2 2 2 1 0 2 0 | 0 1 1 2 0 2 1 0 0 0 1 0 | * 4 * * * tricu
0 2 2 2 | 0 0 0 1 2 2 0 0 2 2 | 0 0 0 0 0 2 0 2 0 1 0 0 | * * 4 * * trip
0 2 2 1 | 0 0 1 0 2 2 0 1 0 2 | 0 0 0 0 1 0 1 2 0 0 0 1 | * * * 4 * squippy
0 0 8 4 | 0 0 0 0 0 0 4 4 8 8 | 0 0 0 0 0 0 0 0 2 4 4 4 | * * * * 1 co
Nice finding, quickfur!
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
Just found another relatively easy-to-find CRF: the bidiminished x4xox (for ease of typing I'm omitting the 3's). Basically, you can cut off a x4xx||x4xo from the x4xox, which gives the monodiminishing; but you can also cut off the antipodal x4xx||x4xo as well, which produces this CRF.
Here's a projection centered on a x4xx cell:
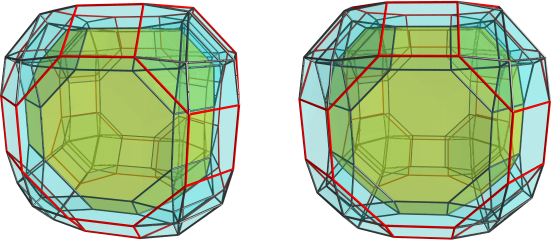
I turned off visibility clipping so that all cells are visible. But it's a bit hard to locate all the cells, though, so here's a slightly different viewpoint:

I turned on visibility clipping here because there's a greater number of overlapping cells otherwise. This projection is centered on one of the x4xo's that remain from the diminishing. This view clearly shows the triangular cupola and triangular prisms that act like "pillars" connecting the top x4xx to the bottom x4xx, interspersed by octagonal prisms.
The cells are: 2 x4xx's (great rhombicuboctahedra), 6 x4xo's (truncated cubes), 16 triangular cupolae, 8 triangular prisms, 12 octagonal prisms. (Please check, I may have counted wrong. )
)
Here are the coordinates:
I'm not sure if Klitzing has already found this one, I seem to recall reading something about tesseract family truncations recently.
Here's a projection centered on a x4xx cell:

I turned off visibility clipping so that all cells are visible. But it's a bit hard to locate all the cells, though, so here's a slightly different viewpoint:

I turned on visibility clipping here because there's a greater number of overlapping cells otherwise. This projection is centered on one of the x4xo's that remain from the diminishing. This view clearly shows the triangular cupola and triangular prisms that act like "pillars" connecting the top x4xx to the bottom x4xx, interspersed by octagonal prisms.
The cells are: 2 x4xx's (great rhombicuboctahedra), 6 x4xo's (truncated cubes), 16 triangular cupolae, 8 triangular prisms, 12 octagonal prisms. (Please check, I may have counted wrong.
 )
)Here are the coordinates:
- Code: Select all
All changes of sign of:
(1, 1+√2, 1+2√2, 1+√2)
(1, 1+2√2, 1+√2, 1+√2)
(1+√2, 1, 1+2√2, 1+√2)
(1+√2, 1+√2, 1+2√2, 1)
(1+√2, 1+2√2, 1, 1+√2)
(1+√2, 1+2√2, 1+√2, 1)
(1+2√2, 1, 1+√2, 1+√2)
(1+2√2, 1+√2, 1, 1+√2)
(1+2√2, 1+√2, 1+√2, 1)
I'm not sure if Klitzing has already found this one, I seem to recall reading something about tesseract family truncations recently.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
quickfur wrote:[...] The cells are: 2 x4xx's (great rhombicuboctahedra), 6 x4xo's (truncated cubes), 16 triangular cupolae, 8 triangular prisms, 12 octagonal prisms. (Please check, I may have counted wrong. ) [...]
I'm not sure if Klitzing has already found this one, I seem to recall reading something about tesseract family truncations recently.
Not that I'd looked into that one in more detail. So, I'd been aware of it surely, as it is just the parabidiminished proh ("pabdiproh"?), and those chopped off caps are known segmentochora. As lace tower it would be described as xxxx3xoox4xwwx&#xt, where w = 1+sqrt(2).
As to the cell counts:
Proh itself has 16 coes, 24 ops, 8 tics, and 32 trips.
Each of those diminishings (tic||girco, K-4.128) has 1 girco, 6 ops, 1 tic, 8 tricues, and 12 trips
Thus pabdiproh should have 16-2*8=0 coes, 0+2*1=2 gircoes, 24-2*6=12 ops, 8-2*1=6 tics, 0+2*8=16 tricues, and 32-2*12=8 trips.
So, your counts were correct this time.

--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
I've discovered a very interesting new CRF that's related to the parabidiminished x4xox.
First, I'd like to note that the x4xox can be augmented with eight x4xo||o4xo's (i.e., truncated_cube||cuboctahedron) -- it just so happens that the result is actually uniform: it's the ox4ox (which is the same as the xo4xo -- cantellated 24-cell). This has the immediate implication that ox4ox has two levels of diminishing possible: you can cut off a x4xo||o4xo -- let's call this simply a diminishing, or you can cut off a bistratic x4xx||x4xo||o4xo, which I'll call a batho-diminishing (from greek batho- meaning deep, i.e., a deep cut).
Now, because of the coincidence of the augmented x4xox with ox4ox, there's a lot more symmetry in the result than the original polychoron, which also means that one can cut the ox4ox in ways that do not correspond with an augmentation of x4xox. That means that if we first augment x4xox into ox4ox, then we can actually do non-parallel bathodiminishings of the result to get something with x4xx cells adjacent to each other. In fact, since the cuboctahedra of ox4ox correspond with the cells of the 24-cell, and bathodiminishings are possible at two given sites if they are meta to each other, it is actually possible to construct a meta-tri-bathodiminished ox4ox, which I have successfully constructed:

This CRF polychoron has a cycle of 3 x4xx's joined to each other via opposite hexagonal faces in one ring, and in the orthogonal ring, an intricate structure of alternating triangular cupolae and square cupolae along with triangular prism bridges. You can somewhat see them girding the x4xx's in the above image.
This appears to be a more intricate version of the tridiminished rectified 24-cell, which I described in this post.
I've just discovered this last night, and I haven't found a good viewpoint that better displays its structure yet -- I'll see if I can find something later today. But at any rate, it was very exciting! This CRF has a very interesting structure!!
First, I'd like to note that the x4xox can be augmented with eight x4xo||o4xo's (i.e., truncated_cube||cuboctahedron) -- it just so happens that the result is actually uniform: it's the ox4ox (which is the same as the xo4xo -- cantellated 24-cell). This has the immediate implication that ox4ox has two levels of diminishing possible: you can cut off a x4xo||o4xo -- let's call this simply a diminishing, or you can cut off a bistratic x4xx||x4xo||o4xo, which I'll call a batho-diminishing (from greek batho- meaning deep, i.e., a deep cut).
Now, because of the coincidence of the augmented x4xox with ox4ox, there's a lot more symmetry in the result than the original polychoron, which also means that one can cut the ox4ox in ways that do not correspond with an augmentation of x4xox. That means that if we first augment x4xox into ox4ox, then we can actually do non-parallel bathodiminishings of the result to get something with x4xx cells adjacent to each other. In fact, since the cuboctahedra of ox4ox correspond with the cells of the 24-cell, and bathodiminishings are possible at two given sites if they are meta to each other, it is actually possible to construct a meta-tri-bathodiminished ox4ox, which I have successfully constructed:

This CRF polychoron has a cycle of 3 x4xx's joined to each other via opposite hexagonal faces in one ring, and in the orthogonal ring, an intricate structure of alternating triangular cupolae and square cupolae along with triangular prism bridges. You can somewhat see them girding the x4xx's in the above image.
This appears to be a more intricate version of the tridiminished rectified 24-cell, which I described in this post.
I've just discovered this last night, and I haven't found a good viewpoint that better displays its structure yet -- I'll see if I can find something later today. But at any rate, it was very exciting! This CRF has a very interesting structure!!
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Hmm, it would seem that this is related to your 4D riddle that you posted some time ago (cf. also the following discussion to that post). It turns out that the bathodiminishings are not restricted to para- positions (in fact, I had thought so earlier too, until I examined the projections of the shallow diminishings and saw that it might be possible to have non-parallel bathodiminishings); it is possible to have bathodiminishings meta to each other. Since the maximal metadiminishing of the 24-cell is the metatridiminishing, the metatribathodiminished ox4ox should also be a maximal bathodiminishing (although I haven't confirmed yet whether more shallow cuts are possible past this point).
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
OK, here are a few more renders of the metatribathodiminished cantellated 24-cell (o3x4o3x). Its structure is more complex than I had realized; there is actually a ring of 6 rhombicuboctahedra (x4ox) orthogonal to the ring of 3 x4xx's. Here's 3 of the x4ox's:

For reference, here are the x4xx's highlighted:
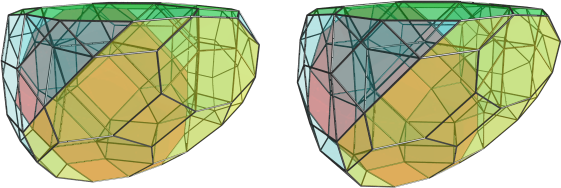
You can see they form a ring around the tubular shape of the polychoron.
The square cupolae, triangular cupolae, and triangular prisms sit between these two rings of cells, acting as the interface between them. This interfacing layer has quite an intricate structure. Here are the cell counts (obtained from my viewer, so they should be correct): 3 x4xx's, 36 triangular prisms, 18 square cupolae, 18 triangular cupolae, 6 x4ox's. Total: 81 cells.
Here are the coordinates (they are kinda long because my coordinate factoring program couldn't find a simple pattern for them):
P.S. All of the above renders have visibility clipping on, because otherwise there are too many tangled edges. That's why the x4xx's shown above are actually only halves of the x4xx's, their volume lies on the far side of the projection (I'm using perspective projection here).

For reference, here are the x4xx's highlighted:

You can see they form a ring around the tubular shape of the polychoron.
The square cupolae, triangular cupolae, and triangular prisms sit between these two rings of cells, acting as the interface between them. This interfacing layer has quite an intricate structure. Here are the cell counts (obtained from my viewer, so they should be correct): 3 x4xx's, 36 triangular prisms, 18 square cupolae, 18 triangular cupolae, 6 x4ox's. Total: 81 cells.
Here are the coordinates (they are kinda long because my coordinate factoring program couldn't find a simple pattern for them):
- Code: Select all
<0, -√2, -√2, ±(2+2*√2)>
<0, √2, ±√2, 2+2*√2>
<0, ±√2, 2+2*√2, -√2>
<0, -√2, -(2+2*√2), ±√2>
<0, √2, ±(2+2*√2), √2>
<0, ±(2+2*√2), √2, -√2>
<0, -(2+2*√2), -√2, ±√2>
<0, 2+2*√2, ±√2, √2>
<±√2, 0, -√2, 2+2*√2>
<±√2, 0, √2, -(2+2*√2)>
<√2, 0, -√2, -(2+2*√2)>
<√2, 0, √2, 2+2*√2>
<±√2, 0, -(2+2*√2), √2>
<±√2, 0, 2+2*√2, -√2>
<√2, 0, -(2+2*√2), -√2>
<√2, 0, 2+2*√2, √2>
<±√2, -√2, 0, -(2+2*√2)>
<±√2, √2, 0, 2+2*√2>
<√2, -√2, 0, 2+2*√2>
<√2, √2, 0, -(2+2*√2)>
<±√2, -√2, -(2+2*√2), 0>
<±√2, √2, 2+2*√2, 0>
<√2, -√2, 2+2*√2, 0>
<√2, √2, -(2+2*√2), 0>
<±√2, -(2+2*√2), 0, -√2>
<±√2, 2+2*√2, 0, √2>
<√2, -(2+2*√2), 0, √2>
<√2, 2+2*√2, 0, -√2>
<±√2, -(2+2*√2), -√2, 0>
<±√2, 2+2*√2, √2, 0>
<√2, -(2+2*√2), √2, 0>
<√2, 2+2*√2, -√2, 0>
<-(2+2*√2), 0, -√2, √2>
<-(2+2*√2), 0, √2, -√2>
<-(2+2*√2), -√2, 0, -√2>
<-(2+2*√2), √2, 0, √2>
<-(2+2*√2), -√2, -√2, 0>
<-(2+2*√2), √2, √2, 0>
<±1, -(1+√2), -(1+√2), ±(1+2*√2)>
<±1, 1+√2, ±(1+√2), 1+2*√2>
<±1, ±(1+√2), 1+2*√2, -(1+√2)>
<±1, -(1+√2), -(1+2*√2), ±(1+√2)>
<±1, 1+√2, ±(1+2*√2), 1+√2>
<±1, ±(1+2*√2), 1+√2, -(1+√2)>
<±1, -(1+2*√2), -(1+√2), ±(1+√2)>
<±1, 1+2*√2, ±(1+√2), 1+√2>
<-(1+√2), ±1, -(1+√2), 1+2*√2>
<-(1+√2), ±1, 1+√2, -(1+2*√2)>
<1+√2, ±1, ±(1+√2), ±(1+2*√2)>
<-(1+√2), ±1, -(1+2*√2), 1+√2>
<-(1+√2), ±1, 1+2*√2, -(1+√2)>
<1+√2, ±1, ±(1+2*√2), ±(1+√2)>
<-(1+√2), -(1+√2), ±1, -(1+2*√2)>
<-(1+√2), 1+√2, ±1, 1+2*√2>
<1+√2, ±(1+√2), ±1, ±(1+2*√2)>
<±(1+√2), -(1+√2), -(1+2*√2), ±1>
<±(1+√2), 1+√2, 1+2*√2, ±1>
<1+√2, -(1+√2), 1+2*√2, ±1>
<1+√2, 1+√2, -(1+2*√2), ±1>
<-(1+√2), -(1+2*√2), ±1, -(1+√2)>
<-(1+√2), 1+2*√2, ±1, 1+√2>
<1+√2, ±(1+2*√2), ±1, ±(1+√2)>
<±(1+√2), -(1+2*√2), -(1+√2), ±1>
<±(1+√2), 1+2*√2, 1+√2, ±1>
<1+√2, -(1+2*√2), 1+√2, ±1>
<1+√2, 1+2*√2, -(1+√2), ±1>
<-(1+2*√2), ±1, -(1+√2), 1+√2>
<-(1+2*√2), ±1, 1+√2, -(1+√2)>
<-(1+2*√2), -(1+√2), ±1, -(1+√2)>
<-(1+2*√2), 1+√2, ±1, 1+√2>
<-(1+2*√2), -(1+√2), -(1+√2), ±1>
<-(1+2*√2), 1+√2, 1+√2, ±1>
P.S. All of the above renders have visibility clipping on, because otherwise there are too many tangled edges. That's why the x4xx's shown above are actually only halves of the x4xx's, their volume lies on the far side of the projection (I'm using perspective projection here).
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Okay, here is the lace city of srico, displaying the axial direction of your interest:
and then, cutting off those bistratic caps (co||tic||girco), it would result in
used lengths here were:
Cell count of srico: 24 coes + 24 sircoes + 96 trips
Cell count of co||tic: 1 co + 6 squacues + 1 tic + 8 trips
Cell count of tic||girco: 1 girco + 6 ops + 1 tic + 8 tricues + 12 trips
i.e. cell count of each diminishing: 1 co + 6 escues + 1 girco + 8 tricues + 20 trips
It should be mentioned here, before adding these numbers, that the tricues are halved coes, for sure. But moreover, the diminishings do not only chop off 1 complete co, but additionally show up 2 tricues exactly at those ridges, which are the commence of the next diminishing. That is of either diminishing 6 tricues are coes into the remainder, but 2 are coes into neighbouring diminishings!
Thus your tridiminishing has:
24-3*8=0 coes + 3*1=3 gircoes + 24-3*6=6 sircoes + 3*6=18 squacues + 3*6=18 tricues + 96-3*20=36 trips
Very nice shape, indeed!
--- rk
- Code: Select all
x3o x3o
w3o
x3x x3x
w3x w3x
o3x o3x
x3w x3w
w3u
o3w x3X x3X o3w
X3x X3x
o3x o3x
u3w u3w
Z3o
x3w o3Z o3Z x3w
X3x X3x
x3x x3x
x3X x3X
w3x Z3o Z3o w3x
o3Z
w3u w3u
x3o x3o
x3X x3X
w3o X3x X3x w3o
u3w
w3x w3x
x3o x3o
x3w x3w
x3x x3x
o3w
o3x o3x
and then, cutting off those bistratic caps (co||tic||girco), it would result in
- Code: Select all
x3x
w3x
x3w
w3u
x3X x3X
X3x X3x
u3w u3w
Z3o
x3w o3Z o3Z
X3x X3x
x3x
x3X x3X
w3x Z3o Z3o
o3Z
w3u w3u
x3X x3X
X3x X3x
u3w
w3x
x3w
x3x
used lengths here were:
- Code: Select all
x = 1
w = x+q = 1+sqrt2
u = 2x = 2
X = 2x+q = 2+sqrt2
Y = x+2q = 1+2sqrt2
Z = 3x+q = 3+sqrt2
Cell count of srico: 24 coes + 24 sircoes + 96 trips
Cell count of co||tic: 1 co + 6 squacues + 1 tic + 8 trips
Cell count of tic||girco: 1 girco + 6 ops + 1 tic + 8 tricues + 12 trips
i.e. cell count of each diminishing: 1 co + 6 escues + 1 girco + 8 tricues + 20 trips
It should be mentioned here, before adding these numbers, that the tricues are halved coes, for sure. But moreover, the diminishings do not only chop off 1 complete co, but additionally show up 2 tricues exactly at those ridges, which are the commence of the next diminishing. That is of either diminishing 6 tricues are coes into the remainder, but 2 are coes into neighbouring diminishings!
Thus your tridiminishing has:
24-3*8=0 coes + 3*1=3 gircoes + 24-3*6=6 sircoes + 3*6=18 squacues + 3*6=18 tricues + 96-3*20=36 trips
... so they should be correct): 3 x4xx's, 36 triangular prisms, 18 square cupolae, 18 triangular cupolae, 6 x4ox's. Total: 81 cells
Very nice shape, indeed!
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
Thinking about the gyrated prismatotruncated pentachoron, I believe that the triangular cupolas and hexagonal prisms should definitely fuse into elongated triangular cupolas...
Now wondering about other possible gyrations of this kind. For example, tetrahedron || cuboctahedron is half a small prismated decachoron and it should be possible to glue two of them together wrong. You get a polychoron with the same cells (10 tetrahedra + 20 triangular prisms), but different connectivity (pseudo-spid?).
The same way, there are two ways to glue two raps together by an octahedron. There's an elongated rap formed by inserting a 3,4-duoprism between two segmentochora forming the rap (point || triangular prism and triangle || dual triangular prism).
Now wondering about other possible gyrations of this kind. For example, tetrahedron || cuboctahedron is half a small prismated decachoron and it should be possible to glue two of them together wrong. You get a polychoron with the same cells (10 tetrahedra + 20 triangular prisms), but different connectivity (pseudo-spid?).
The same way, there are two ways to glue two raps together by an octahedron. There's an elongated rap formed by inserting a 3,4-duoprism between two segmentochora forming the rap (point || triangular prism and triangle || dual triangular prism).
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
Marek14 wrote:Thinking about the gyrated prismatotruncated pentachoron, I believe that the triangular cupolas and hexagonal prisms should definitely fuse into elongated triangular cupolas...
Sorry, I'm unfamiliar with what the term "prismatotruncated" means -- are you talking about a truncated form of x3o3x3o?
EDIT: nevermind, I found your original post, it's the x3x3o3x. Hmm, that's an interesting thought. I know, I'll try to construct it in my modeller and see if the cells come out fused or not!
 I'll let you know the results.
I'll let you know the results.Now wondering about other possible gyrations of this kind. For example, tetrahedron || cuboctahedron is half a small prismated decachoron and it should be possible to glue two of them together wrong. You get a polychoron with the same cells (10 tetrahedra + 20 triangular prisms), but different connectivity (pseudo-spid?).
[...]
Yes, I believe this is possible too. You'll get triangular prisms paired up with triangular prisms, and tetrahedra with tetrahedra, instead of triangular prisms with tetrahedra, at the "equator" of a cuboctahedron cross-section.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
quickfur wrote:Marek14 wrote:Thinking about the gyrated prismatotruncated pentachoron, I believe that the triangular cupolas and hexagonal prisms should definitely fuse into elongated triangular cupolas...
Sorry, I'm unfamiliar with what the term "prismatotruncated" means -- are you talking about a truncated form of x3o3x3o? ...
That is an easy one.
xxoooo... is truncate
xoxooo... is rhombate
xooxoo... is prismate
Then
xxxooo... would be rhombitruncate (Jonathan prefers: great rhombete)
xxoxoo... is prismatotruncate
xoxxoo... is prismatorhombate
Note that in 4D prismatotruncate (from one end) is the same as prismatorhombate (from the other).
Marek uses prismatotruncate. Jonathan prefers here prismatorhombate.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
Marek14 wrote:... Now wondering about other possible gyrations of this kind. For example, tetrahedron || cuboctahedron is half a small prismated decachoron and it should be possible to glue two of them together wrong. You get a polychoron with the same cells (10 tetrahedra + 20 triangular prisms), but different connectivity (pseudo-spid?). ...
Think this is exactly what Norman once called an orthobicupola. (In contrast to the natural one here/there, the gyrobicupola.)
In fact this is xxx3ooo3oxo&#xt.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
Not enough time to check all sources, sorry about that 

- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
Just thought a bit more about quickfur's tribathodiminished srico. (Batho here just means deep. Does not specify the number of stratos however.)
So I looked at srix. Here is a pic from wikipedia, meaning to display a projection; thereby it is nothing but a lace city display (just that the orthogonal space codings are missing):

So it shows clearly that you could chop off a tristratic cap from it. Thought a while, got that it should be: o3x5o || x3x5o || x3o5f || x3x5x. (The third layer would have to use f = tau = golden ratio sized edges. But not doing a section there, would leave that greater structure together.)
And then, as for your bistratic tridiminishing of srico had a lace city display, which was a regular triangle, here too is a tristratic pentadiminishing of srix, which would be displayed as a regular pentagon (connecting the outermost orange dots)!
--- rk
So I looked at srix. Here is a pic from wikipedia, meaning to display a projection; thereby it is nothing but a lace city display (just that the orthogonal space codings are missing):

So it shows clearly that you could chop off a tristratic cap from it. Thought a while, got that it should be: o3x5o || x3x5o || x3o5f || x3x5x. (The third layer would have to use f = tau = golden ratio sized edges. But not doing a section there, would leave that greater structure together.)
And then, as for your bistratic tridiminishing of srico had a lace city display, which was a regular triangle, here too is a tristratic pentadiminishing of srix, which would be displayed as a regular pentagon (connecting the outermost orange dots)!
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
quickfur wrote:Marek14 wrote:Thinking about the gyrated prismatotruncated pentachoron, I believe that the triangular cupolas and hexagonal prisms should definitely fuse into elongated triangular cupolas...
Sorry, I'm unfamiliar with what the term "prismatotruncated" means -- are you talking about a truncated form of x3o3x3o?
EDIT: nevermind, I found your original post, it's the x3x3o3x. Hmm, that's an interesting thought. I know, I'll try to construct it in my modeller and see if the cells come out fused or not!I'll let you know the results.
[...]
OK, I successfully constructed the gyrated x3x3o3x, and verified that it's CRF.
However, the bad news is that the hexagonal prisms do not fuse with the triangular cupola. The hyperplane normal for the triangular cupola is <1,-15/sqrt(15),0,0,-16*sqrt(2/5)>, and the hyperplane normal for the hexagonal prism is <1,-5/sqrt(15),0,0,-12/sqrt(10)>. If I'm not mistaken, that works out to be an angle of 8.9893° between the two hyperplanes. (Please check, since I'm not 100% certain of my calculations: I used the dot product of the two normals to solve for the angle).
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Klitzing wrote:Just thought a bit more about quickfur's tribathodiminished srico. (Batho here just means deep. Does not specify the number of stratos however.)
So I looked at srix. [...] So it shows clearly that you could chop off a tristratic cap from it. Thought a while, got that it should be: o3x5o || x3x5o || x3o5f || x3x5x. (The third layer would have to use f = tau = golden ratio sized edges. But not doing a section there, would leave that greater structure together.)
And then, as for your bistratic tridiminishing of srico had a lace city display, which was a regular triangle, here too is a tristratic pentadiminishing of srix, which would be displayed as a regular pentagon (connecting the outermost orange dots)! [...]
Wow, that's interesting! Funnily enough, somebody (I think it was Mrrl aka Andrey, or maybe Marek) had already discovered the tristratic cap quite a while back, which is now listed under "rotunda" in the wiki's CRF project page, but nobody thought to look at what's left of the original polychoron after the cap was cut off.

Here's another line of investigation that I wanted to do, but so far haven't gotten around to: we know the dodecahedra of the 120-cell can be partitioned into 12 great circles of 10 cells each, which gives us a dodecahedral swirlprism sort of arrangement. Now, it should be possible to map each of these great circles to the x5ox's of the x5o3x3o, so that the x5ox's are partitioned into 12 rings. Then within each ring of x5ox's, we can gyrate (resp. cut off) the 10prism||pentagon segmentochora in between the x5ox's, and so we would obtain the swirlgyrated (resp. swirldiminished) x5oxo, which will have 120 parabigyrated x5ox's (resp. parabidiminished x5ox's).
The only thing I'm not sure about, is whether this gyration (resp. diminishing) is CRF, because I'm not sure if the 10p||5g segmentochora from adjacent rings would overlap, making it impossible to gyrate/delete them without making the result non-CRF. Is this possible?
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Klitzing wrote:[...] So I looked at srix. Here is a pic from wikipedia, meaning to display a projection; thereby it is nothing but a lace city display (just that the orthogonal space codings are missing):
[...]
So it shows clearly that you could chop off a tristratic cap from it. Thought a while, got that it should be: o3x5o || x3x5o || x3o5f || x3x5x. (The third layer would have to use f = tau = golden ratio sized edges. But not doing a section there, would leave that greater structure together.)
And then, as for your bistratic tridiminishing of srico had a lace city display, which was a regular triangle, here too is a tristratic pentadiminishing of srix, which would be displayed as a regular pentagon (connecting the outermost orange dots)! [...]
Another idea occurred to me while looking at the wikipedia diagram: in the case of srix, the diminished caps are far away enough from the other cells, that it may be possible to do the same diminishing on the caps lying in the orthogonal ring and get a CRF result! Then, we should be able to get some kind of intricate structure with 5,5-duoprism symmetry (or derived), with two orthogonal pentagonal arrangements!
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Another thought: I just realized that o5x3o3o can also be diminished to give a pentagonal arrangement of cells, and probably in two orthogonal rings too (if my previous analysis is correct). In this case, there is only a bistratic cap, which is the icosidodecahedral rotunda, but the same principle applies: the key point is that removing the cap whose top is a o5xo, also bisects the 12 o5xo's around that cell, and since 120-cell symmetry has the dodecahedral elements in rings of 10 around great circles, this means each diminishing cuts off 1 cell and 2 halves from the ring, so a ring of 10 can be cut into a ring of 5 in the diminished polychoron.
Anyway, I think I'll try to test my theory of 2 orthogonal pentadiminishings on o5x3o3o, since its coordinates are more manageable, and see if it works. If it doesn't, it wouldn't work on srix either -- there's a possibility that the diminishing in one ring will be too deep and you won't be able to diminish the other ring without making some cells non-CRF.
Anyway, I think I'll try to test my theory of 2 orthogonal pentadiminishings on o5x3o3o, since its coordinates are more manageable, and see if it works. If it doesn't, it wouldn't work on srix either -- there's a possibility that the diminishing in one ring will be too deep and you won't be able to diminish the other ring without making some cells non-CRF.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
What are the possibilities in augmenting duoprisms with 3||6p, 4||8p or 5||10p segmentochora (or line||cube)? If they exist, the possibilities would be enhanced by the fact that each of these can have two orientations (three in case of line || cube)
- Marek14
- Pentonian
- Posts: 1191
- Joined: Sat Jul 16, 2005 6:40 pm
Re: Johnsonian Polytopes
quickfur wrote:[...]Wow, that's interesting! Funnily enough, somebody (I think it was Mrrl aka Andrey, or maybe Marek) had already discovered the tristratic cap quite a while back, which is now listed under "rotunda" in the wiki's CRF project page, but nobody thought to look at what's left of the original polychoron after the cap was cut off.[...]
Just to push my naming concept here:
I use (with respect to parts of larger (orbiform) polytopes, being cut out by 2 parallel hyperplanes)
- cap: any multistratic segment with one hyperplane being tagential
- cupola: in the stricter sense: as was defined in my paper on segmentochora; in a looser sense we could include all lace prisms (i.e. being monostratic!), which have a non-degenerate top base ("top" here will be the smaller one), and are neither prisms nor antiprisms. That is we might include esp. those monostratic caps (which I mentioned in my paper as a different possibility to extrapolate the §D term to).
- rotunda: hemispherical polytopes, i.e. caps, where the other hyperplane happens to be equatorial. (Esp. that tristratic cap of srix, you are refering, clearly is not a rotunda.)
- else: any other part between 2 parallel vertex layers is called (latin style) segment (more specifically also: sub-segment) or just (greek style) stratos. (We could use that term in a narrower sense exclusively, but in a broader sense also inclusively, that is, including caps here as well.)
- segmentotope: is then (in this specific application of consideration) just a monostratic segment (in the inclusive sense). (Note, this bows to my definition of the paper. By the mere ethymology of the word (segment + tope) it would like to include multistratic ones. So we should consider that restriction to monostratic ones as being implied here!)
Rosettes I call polytopes, which are external blends (i.e. adjoins) of several wedges, which close while cycling around the wedge-angle. That is any polytope, being possible to be cut into lunes, trivially is a rosette from its lunes. But there are non-lune wedges too, which might give rise for rosettes. Rosettes further can be specified by the name of a regular polygon/polygram (which lives in the orthospace of that wedge-ridge.
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
quickfur wrote:[...] Here's another line of investigation that I wanted to do, but so far haven't gotten around to: we know the dodecahedra of the 120-cell can be partitioned into 12 great circles of 10 cells each, which gives us a dodecahedral swirlprism sort of arrangement. Now, it should be possible to map each of these great circles to the x5ox's of the x5o3x3o, so that the x5ox's are partitioned into 12 rings. Then within each ring of x5ox's, we can gyrate (resp. cut off) the 10prism||pentagon segmentochora in between the x5ox's, and so we would obtain the swirlgyrated (resp. swirldiminished) x5oxo, which will have 120 parabigyrated x5ox's (resp. parabidiminished x5ox's).
The only thing I'm not sure about, is whether this gyration (resp. diminishing) is CRF, because I'm not sure if the 10p||5g segmentochora from adjacent rings would overlap, making it impossible to gyrate/delete them without making the result non-CRF. Is this possible?
Wow, those are very interesting!

You even could apply that to any such ring individually. Whether such a gyration keeps all angles convex, should be determined. Diminishing clearly would be possible.
As to whether its application to more than 1 ring would lead to intersections of those dips (10p):
Such swirl-cycles are non-intersecting. I.e. it applies to each doe / srid a specific axis, only the top and bottom pentagons do connect to other such shapes of the same ring. Clearly they adjoin at the 10 other pentagons to other does / srids of other rings. But those would not be diminished / gyrated in your case. So, up to the srids (x5o3x .) this would be no problem. - The remainder of these 5g||10p segmentochora would be trips and squippies. Squippies would result from to be halved octs (. o3x3o). Those represent the former vertices of hi. Note that hi has 600 vertices. There would be 12 swirling cycles of 10 does in hi. This comes down to have 120 connecting pentagons. As any such has 5 vertices, we would get 600 vertices in total (if no 2 would be incident to a single vertex). But we just saw that we have 600 possible vertices to be used, i.e. those pentagons will be completely separated! This shows then that the to be dissected octs from srahi too would not interrelate. And further, as the trips of srahi (as: x . x3o) correspond to the edges of hi (as: x . o3o), the critical ones would be those edges of those connecting pentagons. But when the pentagons will not be incident at vertices, they esp. cannot be incident at edges. Thus those trips to be used in that 5g||10p (to be diminished or gyrated) would not interrelate either.
Thus it comes out that all these possible swirling diminishings / gyrations should be possible, in any combination btw.: You just have to select a specific swirl orientation first, then you could separately apply cyclo-diminishings and cyclo-gyrations to either ring independently!
Sure the omni-cases would be esp. interesting, as they have the highest symmetry. But I do not know by hand, whether those 12 rings could be split into 2 or more classes in such a way that there would be a subsymmetry, acting on those transiently. (Okay, 12 classes would be trivial, for sure.)
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
quickfur wrote:Another idea occurred to me while looking at the wikipedia diagram: in the case of srix, the diminished caps are far away enough from the other cells, that it may be possible to do the same diminishing on the caps lying in the orthogonal ring and get a CRF result! Then, we should be able to get some kind of intricate structure with 5,5-duoprism symmetry (or derived), with two orthogonal pentagonal arrangements!
This I spotted too: the grid-section, being displayed to the left as a vertical line (of orange dots) is displayed as an perpendicular central ring (of red dots at the same diameter).
Quite interesting. That srit has a 4,4-dip subsymmetry is widely known. That srix thus would have a 5,5-dip subsymmetry, is new to me (at least).
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
quickfur wrote:Another thought: I just realized that o5x3o3o can also be diminished to give a pentagonal arrangement of cells, and probably in two orthogonal rings too (if my previous analysis is correct). In this case, there is only a bistratic cap, which is the icosidodecahedral rotunda, but the same principle applies: the key point is that removing the cap whose top is a o5xo, also bisects the 12 o5xo's around that cell, and since 120-cell symmetry has the dodecahedral elements in rings of 10 around great circles, this means each diminishing cuts off 1 cell and 2 halves from the ring, so a ring of 10 can be cut into a ring of 5 in the diminished polychoron.
Anyway, I think I'll try to test my theory of 2 orthogonal pentadiminishings on o5x3o3o, since its coordinates are more manageable, and see if it works. If it doesn't, it wouldn't work on srix either -- there's a possibility that the diminishing in one ring will be too deep and you won't be able to diminish the other ring without making some cells non-CRF.
Yep, rox has the same pentagon, inscribed into its projection. The to be chopped of caps (not rotundae
 ) are o3x5o||o3o5f||o3x5x. - So, I cannot spot the vertices of the orthogonal ring of tids in that display (so far).
) are o3x5o||o3o5f||o3x5x. - So, I cannot spot the vertices of the orthogonal ring of tids in that display (so far). 
--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Re: Johnsonian Polytopes
Marek14 wrote:What are the possibilities in augmenting duoprisms with 3||6p, 4||8p or 5||10p segmentochora (or line||cube)? If they exist, the possibilities would be enhanced by the fact that each of these can have two orientations (three in case of line || cube)
Yes, and yes! The reason is that the dihedral angle of the triangle to the square base (resp. triangular/pentagonal base) of a square pyramid (resp. triangle/pentagonal pyramids) is exactly the same as the angle of the triangle to the octagonal base (resp. hexagonal/decagonal base) of the square (triangle/pentagon) cupola. There's the additional square faces that may pose a problem, but that shouldn't matter, because they have the same angle as the apex-to-base edge of the resp. pyramids, so if there were a problem with them, there would also have been a problem with the pyramid-augmented duoprisms in the first place.
This parallel extends also to n-prism pyramid --> n-gon||2n-prism, because the lateral cells are translated from n-pyramids to n-gonal cupola, and since all dihedral angles remain the same, and all heights remain the same, the dichoral angles are also the same. So, this means that every pyramid-augmented m,n-duoprism has a corresponding (n-gon||2n-prism)-augmented m,2n-duoprism.
Moreover, as you note, there are more possibilities here, because the cupola can be rotated in 2 distinct orientations. Here we do have to do an extra check that the angles are still convex after rotation (they may not be, we can't infer this from the pyramid-augments because they can't fit on the n-prisms in rotated orientation).
Now, as for line||cube, two of the orientations will actually have coplanar cells with the prisms on the orthogonal duoprism ring, so they will add square pyramid augments to those cells! So the result can only be convex if the other ring's prisms can be CRF-augmented with square pyramids. So there is some limiting factor here.
- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Klitzing wrote:quickfur wrote:[...]Wow, that's interesting! Funnily enough, somebody (I think it was Mrrl aka Andrey, or maybe Marek) had already discovered the tristratic cap quite a while back, which is now listed under "rotunda" in the wiki's CRF project page, but nobody thought to look at what's left of the original polychoron after the cap was cut off.[...]
Just to push my naming concept here:
I use (with respect to parts of larger (orbiform) polytopes, being cut out by 2 parallel hyperplanes)
- cap: any multistratic segment with one hyperplane being tagential
- cupola: in the stricter sense: as was defined in my paper on segmentochora; in a looser sense we could include all lace prisms (i.e. being monostratic!), which have a non-degenerate top base ("top" here will be the smaller one), and are neither prisms nor antiprisms. That is we might include esp. those monostratic caps (which I mentioned in my paper as a different possibility to extrapolate the §D term to).
- rotunda: hemispherical polytopes, i.e. caps, where the other hyperplane happens to be equatorial. (Esp. that tristratic cap of srix, you are refering, clearly is not a rotunda.)
- else: any other part between 2 parallel vertex layers is called (latin style) segment (more specifically also: sub-segment) or just (greek style) stratos. (We could use that term in a narrower sense exclusively, but in a broader sense also inclusively, that is, including caps here as well.)
- segmentotope: is then (in this specific application of consideration) just a monostratic segment (in the inclusive sense). (Note, this bows to my definition of the paper. By the mere ethymology of the word (segment + tope) it would like to include multistratic ones. So we should consider that restriction to monostratic ones as being implied here!)
The current terminology on the wiki's CRF project page is that "rotunda" refers to any cap that is more than monostratic. It's just a different way of generalizing the 3D term, I guess.
 But maybe your terminology is more consistent. Would you mind updating the wiki to reflect this change?
But maybe your terminology is more consistent. Would you mind updating the wiki to reflect this change?Further we already implemented luna (or just: lune) for wedge-parts being cut out by 2 hyperplanes through vertex layers, which are both equatorial, and esp. not parallel. They further will be specified by the ratio of this dihedral angle between those hyperplanes (based on the full circuit: e.g. an 1/10-lune etc.). Clearly there will be always 2 complementary lunes, which will add to a rotunda (in the above sense) then. (Addition being possibly up to some minor parts, which correspond to some dissected edges etc., thus giving rise to pyramid-diminishings, so that, when adding, kind a rosette will have to re-inserted there.)
Rosettes I call polytopes, which are external blends (i.e. adjoins) of several wedges, which close while cycling around the wedge-angle. That is any polytope, being possible to be cut into lunes, trivially is a rosette from its lunes. But there are non-lune wedges too, which might give rise for rosettes. Rosettes further can be specified by the name of a regular polygon/polygram (which lives in the orthospace of that wedge-ridge.[...]
I was using the term 'florets' for these polychora, but I guess rosette works just as well, too.

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Klitzing wrote:quickfur wrote:Another idea occurred to me while looking at the wikipedia diagram: in the case of srix, the diminished caps are far away enough from the other cells, that it may be possible to do the same diminishing on the caps lying in the orthogonal ring and get a CRF result! Then, we should be able to get some kind of intricate structure with 5,5-duoprism symmetry (or derived), with two orthogonal pentagonal arrangements!
This I spotted too: the grid-section, being displayed to the left as a vertical line (of orange dots) is displayed as an perpendicular central ring (of red dots at the same diameter).
Quite interesting. That srit has a 4,4-dip subsymmetry is widely known. That srix thus would have a 5,5-dip subsymmetry, is new to me (at least).
Klitzing wrote:quickfur wrote:Another thought: I just realized that o5x3o3o can also be diminished to give a pentagonal arrangement of cells, and probably in two orthogonal rings too (if my previous analysis is correct). In this case, there is only a bistratic cap, which is the icosidodecahedral rotunda, but the same principle applies: the key point is that removing the cap whose top is a o5xo, also bisects the 12 o5xo's around that cell, and since 120-cell symmetry has the dodecahedral elements in rings of 10 around great circles, this means each diminishing cuts off 1 cell and 2 halves from the ring, so a ring of 10 can be cut into a ring of 5 in the diminished polychoron.
Anyway, I think I'll try to test my theory of 2 orthogonal pentadiminishings on o5x3o3o, since its coordinates are more manageable, and see if it works. If it doesn't, it wouldn't work on srix either -- there's a possibility that the diminishing in one ring will be too deep and you won't be able to diminish the other ring without making some cells non-CRF.
Yep, rox has the same pentagon, inscribed into its projection. The to be chopped of caps (not rotundae) are o3x5o||o3o5f||o3x5x. - So, I cannot spot the vertices of the orthogonal ring of tids in that display (so far).
--- rk
I'm no longer so sure this is actually possible. Last night I tried to build a model of o5x3o3o with two orthogonal rings diminished, but it was non-CRF. But I haven't checked my work yet, maybe I made a mistake, and there's still a possibility for the bicyclopentadiminishing.
I do know that after performing the diminishing for one ring, there are 60 o5xo's left, of which 50 of them share a face with the x5xo's in the first ring, but 10 of them don't -- presumably, these 10 lie in the orthogonal ring. Since the 10 are isolated from the first ring by a layer of 50 o5xo's, I would expect that it should be possible to perform the diminishing of the second ring in a CRF manner, but when I took the convex hull, I got some non-unit length edges. But as I said, I may have made a mistake -- there are a very large number of cells & vertices, and it's easy to make a mistake when copying and pasting stuff around. Additionally, it may matter *which* 5 cells of the 10 in the second ring are diminished; there may be some dependence on the relative orientations of the two rings here. Last night I only checked one choice; I'll check the other choice today to see if it makes a CRF diminishing.
If this fails, it will probably also imply that the srix doesn't admit a CRF bicyclo diminishing either.

- quickfur
- Pentonian
- Posts: 3025
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
Re: Johnsonian Polytopes
Neither know whether I've writing access, nor how to locate all occurancies...quickfur wrote:[...] But maybe your terminology is more consistent. Would you mind updating the wiki to reflect this change?

(Thus it might be better, when someone would take hands on, who knows what to do... I might provide some guidance, if required, with respect to the contents.)
Florets have 2 rings. One clearly is the flower, a rose is an example of. The other is that of a rapier. And that obviously leads into the wrong direction.I was using the term 'florets' for these polychora, but I guess rosette works just as well, too.

--- rk
- Klitzing
- Pentonian
- Posts: 1649
- Joined: Sun Aug 19, 2012 11:16 am
- Location: Heidenheim, Germany
Who is online
Users browsing this forum: No registered users and 44 guests


