Polyomino (EntityTopic, 5)
From Hi.gher. Space
A polyomino (also spelt polimino and polymino) is a collection of hypercubes joined so that one hypercell of one touches another hypercell of another. Polyominoes are named as follows:
- Monomino - one hypercube.
- Domino - two hypercubes.
- Tromino - three hypercubes.
- Tetromino - four hypercubes.
etc.
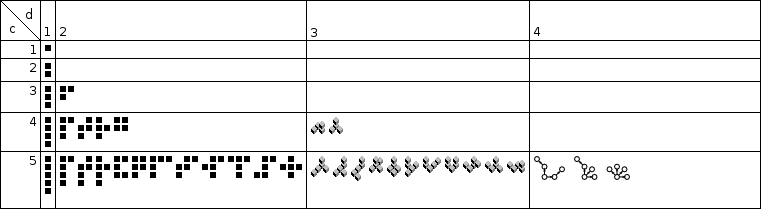
We can generalize sets of polyominoes as p(c,d) where c is the number of hypercubes and d is the number of dimensions.
In n dimensions, there are no new polyominoes that are not simply extrusions of n-1-dimensional polyominoes, if the number of hypercubes is equal to or less than the number of dimensions. In other words, p(c,d) = p(c,d-1) if d ≥ c.
Here is a table of the polyominoes available with various c and d:
Tetrominoes
Tetrominoes are arrangements of four orthogonally-connected cubes. There are seven tetrominoes:
O-block Square block Fat block |  L-block (J-block) Leg block | T-block Tee block |  I-block Line block | Z-block (S-block) Step block | Q-block (G-block) Screw block |  X-block Corner block |
In Tetris, only the first five are available, but since you're only playing in 2D there, two of them are chiral, bringing the count back up to seven again.
The sixth is actually chiral in 3D, so that brings the count up to eight.
Octominoes
There are two special properties about octominoes:
- The first polyomino with a hole is an octomino.
- The first polyomino with no linear symmetry, but rotational symmetry of order 4 is an octomino.