Platonic solids (EntityTopic, 12)
From Hi.gher. Space
Material from http://eusebeia.dyndns.org/4d/ and http://home.comcast.net/~eswab/
The Regular Polyhedra
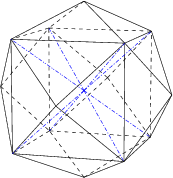
In 3D, we have 5 regular polyhedra, the polyhedra made solely of congruent regular polygons. They are:
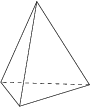
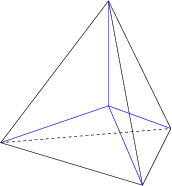
1. The tetrahedron, made of 4 triangles, with 3 meeting at each corner.
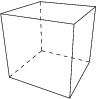
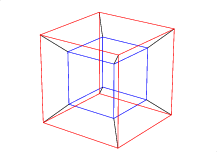
2. The cube, made of 6 squares, with 3 meeting at each corner.
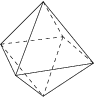
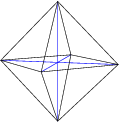
3. The octahedron, made of 8 triangles, with 4 meeting at each corner.
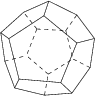
4. The dodecahedron, made of 12 pentagons, with 3 meeting at each corner.
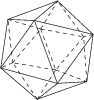
5. The icosahedron, made of 20 triangles, with 5 meeting at each corner.
These are also known as the Platonic solids, and are the only regular polyhedra possible in 3D.
The Regular Polychora
In 4D, we have the regular polychora, which are built from Platonic Solids folded into flunespace. Just as 3D polyhedra are bounded by polygonal faces, 4D polychora are bounded by polyhedral cells. It turns out that there are only 6 possible regular polychora in 4D. They are:
1. The pentachoron, also known as the 5-cell, made of 5 tetrahedra, joined 3 to an edge.
2. The tesseract, the 4D equivalent of a 3D cube, also known as the 8-cell. It is bounded by 8 cubes, joined 3 to an edge.
3. The hexadecachoron, the 4D equivalent of the octahedron. It is bounded by 16 regular tetrahedra joined 4 to an edge.
4. The icositetrachoron, bounded by 24 octahedra. A unique object with no exact analog in any other dimension.
5. The hecatonicosachoron, bounded by 120 regular dodecahedra.
6. The hexacosichoron, bounded by 600 tetrahedra joined 5 to an edge.