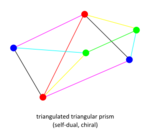
Triangulated triangular prism (EntityTopic, 13)
From Hi.gher. Space
(stub) |
m (+STS Polytope) |
||
| (3 intermediate revisions not shown) | |||
| Line 4: | Line 4: | ||
| dim=3 | | dim=3 | ||
| elements=6, 10, 6 | | elements=6, 10, 6 | ||
| - | }} | + | | sym=[[Chiral biaxial symmetry|C<sub>2</sub>, [2,1]<sup>+</sup>, (22)]] |
| + | | extra={{STS Polytope | ||
| + | | dual=''Self-dual'' | ||
| + | }}}} | ||
The '''triangulated triangular prism''' is one of the [[non-CRF facets of CRF duals]] currently being studied by [[Keiji]]. | The '''triangulated triangular prism''' is one of the [[non-CRF facets of CRF duals]] currently being studied by [[Keiji]]. | ||
| + | |||
| + | Here is a projection based off its appearance in a projection of the [[trixylodiminished hydrochoron]]: | ||
| + | |||
| + | <[#embed [hash HPN8GBRGS3RJYJFMYVA38E8J41]]> | ||
| + | |||
| + | It has [[chiral biaxial symmetry]] C<sub>2</sub>, as can be envisioned by imagining rotating the figure around a line between the midpoints of the leftmost and rightmost edge in the above projection. | ||
| + | |||
| + | When constructed using three edge lengths, ''a'', ''b'' and ''c'' from shortest to longest, it has two [[kite]]s ''aabb'', two isosceles triangles ''abb'' and two isosceles triangles ''bbc''. If ''a'' = ''b'' (turning the kites into squares) then the two ''bbc'' triangles become coplanar and form a [[square]]; if the edge between them is removed a non-uniform [[triangular prism]] results. | ||
<[#polytope [id 51]]> | <[#polytope [id 51]]> | ||
Latest revision as of 15:35, 12 March 2016
The triangulated triangular prism is one of the non-CRF facets of CRF duals currently being studied by Keiji.
Here is a projection based off its appearance in a projection of the trixylodiminished hydrochoron:
It has chiral biaxial symmetry C2, as can be envisioned by imagining rotating the figure around a line between the midpoints of the leftmost and rightmost edge in the above projection.
When constructed using three edge lengths, a, b and c from shortest to longest, it has two kites aabb, two isosceles triangles abb and two isosceles triangles bbc. If a = b (turning the kites into squares) then the two bbc triangles become coplanar and form a square; if the edge between them is removed a non-uniform triangular prism results.
Incidence matrix
Dual: Self-dual
| # | TXID | Va | Vb | Vc | Ea | Eb | Ec | Ed | Ee | Ef | 3a | 3b | 4a | Type | Name |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Va | = point | ; | ||||||||||||
| 1 | Vb | = point | ; | ||||||||||||
| 2 | Vc | = point | ; | ||||||||||||
| 3 | Ea | 2 | 0 | 0 | = digon | ; | |||||||||
| 4 | Eb | 1 | 0 | 1 | = digon | ; | |||||||||
| 5 | Ec | 0 | 1 | 1 | = digon | ; | |||||||||
| 6 | Ed | 1 | 0 | 1 | = digon | ; | |||||||||
| 7 | Ee | 1 | 1 | 0 | = digon | ; | |||||||||
| 8 | Ef | 0 | 2 | 0 | = digon | ; | |||||||||
| 9 | 3a | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | = triangle | ; | |||
| 10 | 3b | 2 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | = triangle | ; | |||
| 11 | 4a | 1 | 2 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | = square | ; | |||
| 12 | C1a | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | = triangulated triangular prism | ; |
Usage as facets
- 72× 1-facets of a trixylodiminished hydrochoron
- 16× 1-facets of a (dual of 4D analog of J37)
- 32× 1-facets of a (dual of 4D analog of J37)
- 12× 1-facets of a (dual of triangular hebesphenorotundaeic rhombochoron)