Platonic solids (EntityTopic, 12)
From Hi.gher. Space
m (Platonic Solids moved to Platonic solids: case) |
m (ontology) |
||
| (5 intermediate revisions not shown) | |||
| Line 1: | Line 1: | ||
| - | ''Material from http://eusebeia.dyndns.org and http:// | + | <[#ontology [kind topic] [cats Essays Regular Polytope]]> |
| + | ''Material from http://eusebeia.dyndns.org/4d/ and http://home.comcast.net/~eswab/'' | ||
== The Regular Polyhedra == | == The Regular Polyhedra == | ||
| Line 7: | Line 8: | ||
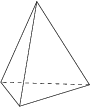
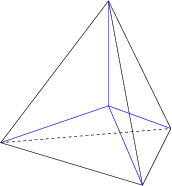
1. The [[tetrahedron]], made of 4 [[triangle]]s, with 3 meeting at each corner. | 1. The [[tetrahedron]], made of 4 [[triangle]]s, with 3 meeting at each corner. | ||
| - | <blockquote> | + | <blockquote><[#embed [hash H2M40HHTSX58TN59G0RB8Y8KG0]]></blockquote> |
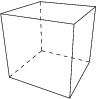
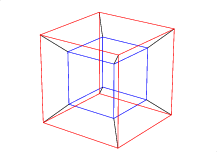
2. The [[cube]], made of 6 [[square]]s, with 3 meeting at each corner. | 2. The [[cube]], made of 6 [[square]]s, with 3 meeting at each corner. | ||
| - | <blockquote> | + | <blockquote><[#embed [hash CZSDWGEHGT1TP5K1WSKTWTNCY9]]></blockquote> |
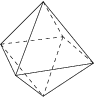
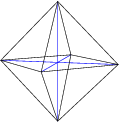
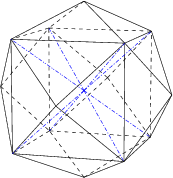
3. The [[octahedron]], made of 8 triangles, with 4 meeting at each corner. | 3. The [[octahedron]], made of 8 triangles, with 4 meeting at each corner. | ||
| - | <blockquote> | + | <blockquote><[#embed [hash 1C88PC9E5CNB8BX2XCENWTGBQK]]></blockquote> |
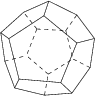
4. The [[dodecahedron]], made of 12 [[pentagon]]s, with 3 meeting at each corner. | 4. The [[dodecahedron]], made of 12 [[pentagon]]s, with 3 meeting at each corner. | ||
| - | <blockquote> | + | <blockquote><[#embed [hash 8DVMY0VJMJYVGZGE5B99PCSR2Y]]></blockquote> |
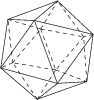
5. The [[icosahedron]], made of 20 triangles, with 5 meeting at each corner. | 5. The [[icosahedron]], made of 20 triangles, with 5 meeting at each corner. | ||
| - | <blockquote> | + | <blockquote><[#embed [hash DQ46RJYTB730G2YBX2BVGR4T7K]]></blockquote> |
These are also known as the '''Platonic solids''', and are the only regular polyhedra possible in 3D. | These are also known as the '''Platonic solids''', and are the only regular polyhedra possible in 3D. | ||
| Line 33: | Line 34: | ||
1. The [[pentachoron]], also known as the ''5-cell'', made of 5 tetrahedra, joined 3 to an edge. | 1. The [[pentachoron]], also known as the ''5-cell'', made of 5 tetrahedra, joined 3 to an edge. | ||
| - | <blockquote> | + | <blockquote><[#embed [hash S0R7JFD37RG7C6QM7T1JGVJZBW]]></blockquote> |
2. The [[tesseract]], the 4D equivalent of a 3D cube, also known as the ''8-cell''. It is bounded by 8 cubes, joined 3 to an edge. | 2. The [[tesseract]], the 4D equivalent of a 3D cube, also known as the ''8-cell''. It is bounded by 8 cubes, joined 3 to an edge. | ||
| - | <blockquote> | + | <blockquote><[#embed [hash TT3H2PWY4MWRR8QYJ30KYK4P55]]></blockquote> |
3. The [[hexadecachoron]], the 4D equivalent of the octahedron. It is bounded by 16 regular tetrahedra joined 4 to an edge. | 3. The [[hexadecachoron]], the 4D equivalent of the octahedron. It is bounded by 16 regular tetrahedra joined 4 to an edge. | ||
| - | <blockquote> | + | <blockquote><[#embed [hash WY51RCQC23FNJ7Q6S2PFMBGK15]]></blockquote> |
4. The [[icositetrachoron]], bounded by 24 octahedra. A unique object with no exact analog in any other dimension. | 4. The [[icositetrachoron]], bounded by 24 octahedra. A unique object with no exact analog in any other dimension. | ||
| - | <blockquote> | + | <blockquote><[#embed [hash 16BH2VARWZXVY792BSCQ8Z7GNP]]></blockquote> |
5. The [[hecatonicosachoron]], bounded by 120 regular dodecahedra. | 5. The [[hecatonicosachoron]], bounded by 120 regular dodecahedra. | ||
| - | <blockquote> | + | <blockquote><[#embed [hash SMTRWY2GWJSGP78SWS19J42D5J]]></blockquote> |
6. The [[hexacosichoron]], bounded by 600 tetrahedra joined 5 to an edge. | 6. The [[hexacosichoron]], bounded by 600 tetrahedra joined 5 to an edge. | ||
| - | <blockquote> | + | <blockquote><[#embed [hash JJHBRY386S0NYHXTTMJYM6KXBS]]></blockquote> |
| - | + | ||
| - | [[ | + | |
Latest revision as of 22:46, 11 February 2014
Material from http://eusebeia.dyndns.org/4d/ and http://home.comcast.net/~eswab/
The Regular Polyhedra
In 3D, we have 5 regular polyhedra, the polyhedra made solely of congruent regular polygons. They are:
1. The tetrahedron, made of 4 triangles, with 3 meeting at each corner.
2. The cube, made of 6 squares, with 3 meeting at each corner.
3. The octahedron, made of 8 triangles, with 4 meeting at each corner.
4. The dodecahedron, made of 12 pentagons, with 3 meeting at each corner.
5. The icosahedron, made of 20 triangles, with 5 meeting at each corner.
These are also known as the Platonic solids, and are the only regular polyhedra possible in 3D.
The Regular Polychora
In 4D, we have the regular polychora, which are built from Platonic Solids folded into flunespace. Just as 3D polyhedra are bounded by polygonal faces, 4D polychora are bounded by polyhedral cells. It turns out that there are only 6 possible regular polychora in 4D. They are:
1. The pentachoron, also known as the 5-cell, made of 5 tetrahedra, joined 3 to an edge.
2. The tesseract, the 4D equivalent of a 3D cube, also known as the 8-cell. It is bounded by 8 cubes, joined 3 to an edge.
3. The hexadecachoron, the 4D equivalent of the octahedron. It is bounded by 16 regular tetrahedra joined 4 to an edge.
4. The icositetrachoron, bounded by 24 octahedra. A unique object with no exact analog in any other dimension.
5. The hecatonicosachoron, bounded by 120 regular dodecahedra.
6. The hexacosichoron, bounded by 600 tetrahedra joined 5 to an edge.