- Code: Select all
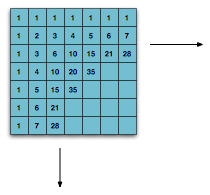
1 1 1 1 1 1 1 ...
1 2 3 4 5 6 ...
1 3 6 10 15 ...
1 4 10 20 ...
1 5 15 ...
1 6 ...
1 ...
...
Now, because I wrote it on its side, the coefficients of the terms in (a+b)<sup>n</sup> are in the n+1-th diagonal. So, for example:
(a+b)<sup>3</sup> = a<sup>3</sup> + 3a<sup>2</sup>b + 3ab</sup>2</sup> + b<sup>3</sup>.
For those that haven't seen Pascal's triangle before, each entry is the sum of the entry above it and the entry to its left.
You can think of the n-th diagonal as the coefficients of the terms in (a+b)<sup>(n-1)</sup> so long as you consider the j-th column to indicate that a is to the (j-1)-th power and the k-th row to indicate that b is to the (k-1)-th power.
Anyhow, that's all well and good. But, what if we had (a+b+c)<sup>n</sup>?
Before we get to that, let's look at the easier case where we have (a)<sup>n</sup>. Then, the coefficients are:
- Code: Select all
1 1 1 1 1 1 ...
That is exactly the same as the first row in Pascal's triangle if you write Pascal's triangle on its side as I did.
Now, let's get back to (a+b+c)<sup>n</sup>. Let's try a few cases.
(a+b+c)<sup>1</sup> yields a + b + c. This means the coefficients are 1, 1, and 1. For n = 2, we get a<sup>2</sup> + b<sup>2</sup> + c<sup>2</sup> + 2ab + 2ac + 2bc. This means we have coefficients 1, 1, 1, 2, 2, 2. For n = 3, we get coefficients 1, 1, 1, 3, 3, 3, 3, 3, 3, and 6.
For n = 4, we get coefficients 1, 1, 1, 4, 4, 4, 4, 4, 4, 6, 6, 6, 12, 12, and 12. What's the pattern here?
If we look at the diagonals of Pascal's triangle. And, if we think of putting a box around each number, then we can start with an unlablelled quarter-plane full of boxen. We can fill in the top-corner with a 1. Then, we can fill in each blank box with the sum of the box adjacent above it and the box adjacent to its left. Lather, rinse, repeat:
If we repeat this process except in three-dimensions, then we'll start with an octant (1/8-th of a realm) full of boxen. We'll do the same thing. We'll fill in the corner with a one. Then, we'll fill in all of the boxen with the sum of its neighbors above, to the left, and behind. We'll end up starting off like this:
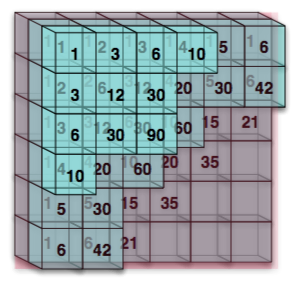
You'll notice that the axises are the coefficients from the a<sup>n</sup> case and the axis-planes are exactly the Pascal triangle from the previous diagram.
You'll also notice that the first diagonal plane through a box center goes through the center of a box labelled 1. The second diagonal plane through box centers goes through the centers of boxen labelled 1, 1, and 1. The third goes through the centers of boxen labelled 1, 1, 1, 2, 2, and 2. The fourth goes through the centers of boxen labelled 1, 1, 1, 3, 3, 3, 3, 3, 3, and 6. The fifth goes through the centers of boxen labelled 1, 1, 1, 4, 4, 4, 4, 4, 4, 6, 6, 6, 12, 12, and 12. Do these look familiar? These were the n = 0, 1, 2, 3, and 4 cases of (a+b+c)<sup>n</sup>.
You can think of the n-th diagonal plane through box centers as the coefficients of the terms in (a+b+c)<sup>(n-1)</sup> so long as you consider the j-th column to indicate that a is to the (j-1)-th power and the k-th row to indicate that b is to the (k-1)-th power and the m-th level to indicate that c is to the (m-1)-th power.
It's relatively straightforward to prove by induction that if you carry this process out in k dimensions, then you're building the coefficients of (a<sub>1</sub>+a<sub>2</sub>+...+a<sub>k</sub>)<sup>n</sup>.
Now, this post is already getting long, so I'm going to cut out here before I get to what's up my sleeve. Actually, I suppose this was already somewhat up my sleeve since cubes stack nicely in all dimensions. But, alas, I have something else up my sleeve.... I'll get to that in a moment.