Don't know if anybody still follows this thread, but I've posted the next Catalan solid on my website:

This is, of course, the
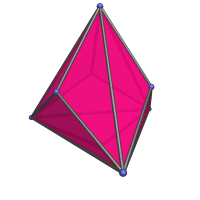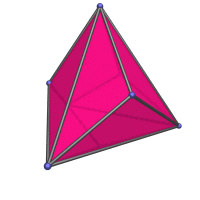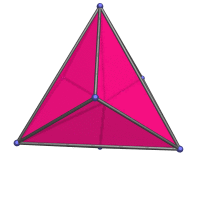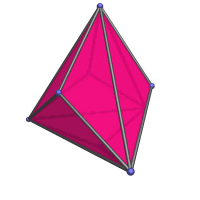
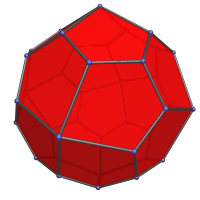
rhombic dodecahedron, which everybody here should already know about. But it's nice to finally have an actual page to link to in the various mentions of the rhombic dodecahedron, like in the projection of the tesseract and the 24-cell.
That, and also I'm using these relatively simple 3D catalans as buffer to work on the pages for the 4D catalans.

Well, relatively simple except for the pentagonal icositetrahedron (dual of the snub cube), which needed a bit of work to wrangle with due to the cubic equations involved, and the pentagonal hexecontahedron (dual of the snub dodecahedron), which gave me a big headache for maybe a week or two because it involves 12th degree polynomials (square roots of cubics involving the golden ratio). I'm still not 100% sure I've completely picked it apart yet, but at least I've figured out enough to have algebraic expressions for its coordinates and edge length ratios. The pages for all the catalans are in fact already ready, I'm just publishing them one per month.
I'm also doing the duals of uniform prisms and antiprisms, and already one of them will definitely feature as cells in one of the 4D catalans, with at least another one that I suspect will also be cells to another 4D catalan.




 )
)





 But anyway, here's this month's:
But anyway, here's this month's:
 I've never seen a definition of "scalene" for anything other than triangles.
I've never seen a definition of "scalene" for anything other than triangles.