Traversable Klein 'bottle' paths
Re: Traversable Klein 'bottle' paths
I think there are no invariant planes to be found, because the toroidal rotation involves a deformation and is not a solid rotation. More precisely, the invariant directions are dependent on the location on the strip.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Traversable Klein 'bottle' paths
Teragon wrote:I think there are no invariant planes to be found, because the toroidal rotation involves a deformation and is not a solid rotation. More precisely, the invariant directions are dependent on the location on the strip.
I'm guessing that that means that you don't think it is a valid representation? Thank you for your patience Teragon. Let's keep exploring it and see...
I've just got to head off to a singing gig this morning. After I get back I'll hopefully add some more.
...I forgot I can use the internet on the train's free WiFi...
Teragon wrote:You have to keep in mind that such a turn in 4D involves an exchange of ana and kata. You can change left and right in 3D too if you turn head over heals. In this case up and down are exchanged. For us 3D beings a 180° through ana/kata would seem like a mirror operation, if that is what you mean.
Correct by my reckoning too.
I would also say that the effect of swapping left and right by flipping 'through' ourself sideways in this way would be the same as if the object were to flip 'through' itself sideways in this way.
No doubt our computers can even flip the whole environment from left to right because we are unlikely to do that ourselves.
I'm using the word 'flip' for something that can't occur in our 3D environment except by simulation (computer, glasses) but I think it's a useful stepping tool for this discussion.
I'm not sure you agree that this 'flipping' is useful Teragon but I hope I can make it otherwise...
Teragon wrote:I thought we were talking about invariant planes.
We are as part of the discussion hopefully towards our goal...
Teragon wrote:I think there are no invariant planes to be found, because the toroidal rotation involves a deformation and is not a solid rotation. More precisely, the invariant directions are dependent on the location on the strip.
I would agree that there is no invariant plane in my animation. I still like discussing the idea with you and it has helped me to understand better what I am doing.
There is something invariant and so I'm leading to discussing whether that is valid...
Teragon wrote:If a 3D object is rotated through a 2D plane, a 2D beeing inside of it may not decide if it's going to the left side or to the right side, but
- it's able to tell if its sense of rotation changes if the object looks different on the left side and the right side, i.e. the 2D plane is not a mirror plane of the object.
- it's able to tell if the object has been flipped by 180° if the rotational axis is not a "mirror axis" of the object, because two directions in the plane will changes parts.
Agree. Those two statements are very similar aren't they (just in case I'm reading them wrong)?
I don't want to get too far ahead without diagrams - though words are always wonderful; pictures can say much more - so I'll wait till I get home to progress further.
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Traversable Klein 'bottle' paths
gonegahgah wrote:I'm guessing that that means that you don't think it is a valid representation?
Quite the opposite, I think it's a valid and potentially valuable way to visualize 4D toroidal objects, something I didn't even consider as a possibility before. It's just important to state what exactly is shown, so that people can learn from it and won't get confused.
gonegahgah wrote:Teragon wrote:If a 3D object is rotated through a 2D plane, a 2D beeing inside of it may not decide if it's going to the left side or to the right side, but
- it's able to tell if its sense of rotation changes if the object looks different on the left side and the right side, i.e. the 2D plane is not a mirror plane of the object.
- it's able to tell if the object has been flipped by 180° if the rotational axis is not a "mirror axis" of the object, because two directions in the plane will changes parts.
Agree. Those two statements are very similar aren't they (just in case I'm reading them wrong)?
They're somewhat different. If the plane where the 3D object intersects the 2D world is no mirror plane of the object (with respect to left and right), it's still possible that the backward and the foreward side of the object look the same and the 2D being can't distinguish between the object and the object with back and front side switched (turned by 180°). Also the opposite is possible, namely that left and right look the same, but front and back sides are distinguishable.
Take this bottle for example (that's what I found on the quick on the internet). A 2D being in the plane wouldn't notice any difference between a clockwise and a counterclockwise rotation of the bottle onto its head (with the rotational axis being the back-forth axis). Still the picture ends reversed when the bottle is turned by 180°.

Here's also an example for the opposite case. When the object rotating clockwise, the top is going to show up on the righthand- side of the plane, rotating counterclockwise it's gonna show up on the left-hand side. A 180° rotation is indistinguishable from the initial orientation though. The interesting thing is, if the top was in the down-direction at first and the rotation was the other way round, it would look exactly the same on the 2D plane.

What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Traversable Klein 'bottle' paths
Cool, thanks Teragon  I've grown to understand it better thanks to your help and can distinguish it better now.
I've grown to understand it better thanks to your help and can distinguish it better now.
Ah now I see with those two examples. It is interesting the last one in that respect.
Continuing our look at invariant planes...
Here's a depiction of our Klein strip at my 90° & 270° but this one is rotated in the conventional way around the x and w pane.

Again I've slightly off-stepped the 3D slices across the 4D space to give them more clarity with each colour representing a 3D slice. The morphing effect is just a result of our being in a 3D world and not 4D.
We can see for this that the invariant plane is x/w plane through their middle of the shape (is that correct Teragon?).
As a next step, I just want to discuss further on 'flipping'. I want to bring that forward into the 3D/4D situation.
First though it's interesting to note with the 'flip' what the invariant is. When we 'rotate' in 3D the invariant is a line but when we 'flip' so that we are seeing everything as a mirror image then in 3D the invariant is a plane...
That is the one thing that stays the same. So in the bottle image you found Teragon, if this were an example of a flip, then the flip would occur through the bisection of the bottle.

It doesn't have to be a bisection though and the flip will always be through the common cross-section at the mirror plane.
Here is an interesting slightly different example.

In this one we can see that the 3D shape intersects the 2D plane in two places but one of the intersections only touches the 2D plane.
You can either then consider there to be an intersection or not. A flip will give the same result anyway.
There is a reason I was curious about this which I will point out later on.
Getting to the 4Der. When a 4Der is in their space they have an extra degree of freedom that we don't have. They can rotate while maintaining up and forward.
This is where I contrast the example you gave Teragon, where we can 'flip' by standing on our head. When we do this we can't maintain the up orientation in our 3D world.
Also, I was saying before it doesn't matter which of the 4Der's directions are left,right,ana,kata just as long as they are opposite for the pairs or those then perpendicular to each other.
So if we take our 4Der who has 3 arms equally spaced beside each other we can still use them to mark left and right; even if the 4Der doesn't understand what left and right are...
We'll paint the letter R on one of those three arms and that will be axis that is right. Left will be opposite this and ana/kata will be perpendicular to this while not being up/down nor forward/back.
So we draw our 3D representation of their world as per their current up and forward and as per their arm which shows right and make the other directions in relation to that right arm.
That's all good. Now we get the 4Der to spin to a certain distance while maintaining up and forward.
After this right is pointing in a different direction than before and we have to redraw our image in relation to that.
The interesting thing is that this is very like flipping a 3D image for a 2Der. The reason is that all points maintain their distance from the y,z plane like they do when we 'flip' x-wise in 3D.
But in a 4D world they can take a rotating journey because all points maintain their distance relative to the y,z plane.
What this does is allow us to simulate all the orientations that a 4Der will experience.
(It also happens to be the easiest way for us to get a good look at a 4D object in 3D using rotational projection).

Here's an attempt to convey that idea.
The blue line is the up or sky axis, the green is the forward axis and the red is our current left-right axis. The brown is the ana-kata axis that is outside our slice.
I drew L-R/A-K curved to depict the equidistance of points from the U-D/F-B.
The left-right we see in our slice are rotated around as per the 4Der's world (with ana-kata consequently following) so that we can get a fuller perspective of the object in 4D from front on.
Now, of course the 4Der would just see this all as a whole; but we don't have that luxury. But, using this process, I think, gives us a better sense of the 4Der's object.
That still remains to be seen when one day hopefully the idea is put into practice (aka as program code).
I have a feeling that the following animation of the Klein Strip is an example of this process...

Apart from checking all that above for me Teragon, if you would please, I was wondering if you could check the following separate thought for me?
In our 2D world we can't rotate toroid like because the inside of the toroid is shorter than the outside.
If you tried that with a donut the inside would split as it stretches to the outside and the outside would squash as it tries to go through inside.
In a 4D world this may not be the case and there may be a path that a donut can follow the allows the inside to remain short while the outside maintains its longer length.
So, I'm wondering if you could actually rotate a donut through its centre along all its length at once in 4D without stressing the donut at all.
It doesn't effect the topic at hand but I am curious... What does everything think about that? Is that last idea very very wrong?
 I've grown to understand it better thanks to your help and can distinguish it better now.
I've grown to understand it better thanks to your help and can distinguish it better now.Ah now I see with those two examples. It is interesting the last one in that respect.
Continuing our look at invariant planes...
Here's a depiction of our Klein strip at my 90° & 270° but this one is rotated in the conventional way around the x and w pane.

Again I've slightly off-stepped the 3D slices across the 4D space to give them more clarity with each colour representing a 3D slice. The morphing effect is just a result of our being in a 3D world and not 4D.
We can see for this that the invariant plane is x/w plane through their middle of the shape (is that correct Teragon?).
As a next step, I just want to discuss further on 'flipping'. I want to bring that forward into the 3D/4D situation.
First though it's interesting to note with the 'flip' what the invariant is. When we 'rotate' in 3D the invariant is a line but when we 'flip' so that we are seeing everything as a mirror image then in 3D the invariant is a plane...
That is the one thing that stays the same. So in the bottle image you found Teragon, if this were an example of a flip, then the flip would occur through the bisection of the bottle.

It doesn't have to be a bisection though and the flip will always be through the common cross-section at the mirror plane.
Here is an interesting slightly different example.

In this one we can see that the 3D shape intersects the 2D plane in two places but one of the intersections only touches the 2D plane.
You can either then consider there to be an intersection or not. A flip will give the same result anyway.
There is a reason I was curious about this which I will point out later on.
Getting to the 4Der. When a 4Der is in their space they have an extra degree of freedom that we don't have. They can rotate while maintaining up and forward.
This is where I contrast the example you gave Teragon, where we can 'flip' by standing on our head. When we do this we can't maintain the up orientation in our 3D world.
Also, I was saying before it doesn't matter which of the 4Der's directions are left,right,ana,kata just as long as they are opposite for the pairs or those then perpendicular to each other.
So if we take our 4Der who has 3 arms equally spaced beside each other we can still use them to mark left and right; even if the 4Der doesn't understand what left and right are...
We'll paint the letter R on one of those three arms and that will be axis that is right. Left will be opposite this and ana/kata will be perpendicular to this while not being up/down nor forward/back.
So we draw our 3D representation of their world as per their current up and forward and as per their arm which shows right and make the other directions in relation to that right arm.
That's all good. Now we get the 4Der to spin to a certain distance while maintaining up and forward.
After this right is pointing in a different direction than before and we have to redraw our image in relation to that.
The interesting thing is that this is very like flipping a 3D image for a 2Der. The reason is that all points maintain their distance from the y,z plane like they do when we 'flip' x-wise in 3D.
But in a 4D world they can take a rotating journey because all points maintain their distance relative to the y,z plane.
What this does is allow us to simulate all the orientations that a 4Der will experience.
(It also happens to be the easiest way for us to get a good look at a 4D object in 3D using rotational projection).

Here's an attempt to convey that idea.
The blue line is the up or sky axis, the green is the forward axis and the red is our current left-right axis. The brown is the ana-kata axis that is outside our slice.
I drew L-R/A-K curved to depict the equidistance of points from the U-D/F-B.
The left-right we see in our slice are rotated around as per the 4Der's world (with ana-kata consequently following) so that we can get a fuller perspective of the object in 4D from front on.
Now, of course the 4Der would just see this all as a whole; but we don't have that luxury. But, using this process, I think, gives us a better sense of the 4Der's object.
That still remains to be seen when one day hopefully the idea is put into practice (aka as program code).
I have a feeling that the following animation of the Klein Strip is an example of this process...

Apart from checking all that above for me Teragon, if you would please, I was wondering if you could check the following separate thought for me?
In our 2D world we can't rotate toroid like because the inside of the toroid is shorter than the outside.
If you tried that with a donut the inside would split as it stretches to the outside and the outside would squash as it tries to go through inside.
In a 4D world this may not be the case and there may be a path that a donut can follow the allows the inside to remain short while the outside maintains its longer length.
So, I'm wondering if you could actually rotate a donut through its centre along all its length at once in 4D without stressing the donut at all.
It doesn't effect the topic at hand but I am curious... What does everything think about that? Is that last idea very very wrong?
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Traversable Klein 'bottle' paths
I've upgraded to the following animation. The only problem is that it causes me more questions instead of answers.

All that has changed is that I show how the Up and Forward axis rotate around themselves (along with the plane they form of course)...

All that has changed is that I show how the Up and Forward axis rotate around themselves (along with the plane they form of course)...
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Traversable Klein 'bottle' paths
gonegahgah wrote:We can see for this that the invariant plane is x/w plane through their middle of the shape (is that correct Teragon?).
Yes, although I don't know where the morphing effect comes from as the colors represent the distance in the w-direction and I'd expect the w-coordinate to be constant.
gonegahgah wrote:That's all good. Now we get the 4Der to spin to a certain distance while maintaining up and forward.
After this right is pointing in a different direction than before and we have to redraw our image in relation to that.
The interesting thing is that this is very like flipping a 3D image for a 2Der. The reason is that all points maintain their distance from the y,z plane like they do when we 'flip' x-wise in 3D.
You mean like flipping a 3D image in 3D? A 4D object rotated by 180° in the xw-plane looks the same to a 3D beeing as an image of it mirrored in the yz-plane. Flipping changes one coordinate only, while spinning changes pairs of coordinates.
gonegahgah wrote:In our 2D world we can't rotate toroid like because the inside of the toroid is shorter than the outside.
If you tried that with a donut the inside would split as it stretches to the outside and the outside would squash as it tries to go through inside.
In a 4D world this may not be the case and there may be a path that a donut can follow the allows the inside to remain short while the outside maintains its longer length.
So, I'm wondering if you could actually rotate a donut through its centre along all its length at once in 4D without stressing the donut at all.
It doesn't effect the topic at hand but I am curious... What does everything think about that? Is that last idea very very wrong?
Yes, that's perfectly possible! But it's already possible for Moebius strips in 3D which also have a flat surface.
Just when I think I understand your original animation for the most part, some realization tells me that everything is different. My considerations about invariant elements led me to the conclusion that the invariant element of a toroidal rotation in 4D is a lateral cylinder surface.

At a closer look it turns out that this is not the case for your first animation.

Really don't know what's going on here. I'd like to take a look at the code you used, if that's possible, gonegahgah.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Traversable Klein 'bottle' paths
Teragon wrote:Really don't know what's going on here.
Me too Teragon. I'm in the process of creating some diagrams that should help clear things up for me; though I'm not sure if I'm liking the results...
I'll post those on here soon and get the formulas to you too. Time for sleep!
[Edit...]
Actually, no panic. I think it may still be okay.
The process I am drawing takes 5 steps: first the starting point and then four rotations...
I'm sure there must be a simpler series of steps...
I did have another interesting realisation yesterday, which we haven't mentioned yet, and that may be what is needed to simplify the steps.
I'll finish drawing the change steps, which are straight forward rotations, soon and post them to get you to check that they are correct Teragon.
They seem to be okay at the moment though I've only drawn three of the five.
I'm out all day tomorrow so I'll try to add them tomorrow night...
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Traversable Klein 'bottle' paths
gonegahgah wrote:The same would occur for us if we were able to magically transfer our whole body from left to right.
Suddenly our brain would see what was on the left as being on the right and vice-versa (this is nothing to do with VRI in case anyone is watching).
Sadly we can't do that but a 4Der can. Also, if we were in a 4D space we could do it to by rotating our 3D slice around 180°. We could flip our body 180° effectively so that left is now right and right is now left.
Since you mentioned it gonegahgah, I thought I'd just pop in and say thank you very much for all the work you and others are doing in this thread, and for mentioning VRIs and yes, I am watching.

Just to clarify, my idea says that we may actually be at least 4Der's in a 4D universe, so the space all around us, seen in a limited viewpoint 3D slice, can be viewed by a full circle of 360° but only in one direction at a time. So when we look at a building in front of us, we can actually see the 3D slice viewpoint of it from different directions using VRIs because it, and we may actually exist in more than just 3 dimensions.

(If anyone wants to discuss VRIs further they can do it in this thread here on the forum: http://hi.gher.space/forum/viewtopic.php?t=401 , thanks.)
My VRI channel: http://youtube.com/channel/UCntWMVVl5wKCx_6CH33_mXg
-

Hugh - Tetronian
- Posts: 817
- Joined: Tue Sep 27, 2005 11:44 pm
Re: Traversable Klein 'bottle' paths
Hi Hugh, good to see you.
I found an error. Hmmm.
I found an error. Hmmm.
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Traversable Klein 'bottle' paths
I'm guessing now that the following are the 0° and 90° versions of Klein Strips but that they are not part of the same object.


I'll explain these pictures...
They are representing the plane that the Klein Strip ring is lying in as the x,y plane.
We can only see the x/y/z planes in a 3D slice so these are shown darker. The w space is shown as more transparent. The front circle cross-section of the Klein Strip is shown as red and the back circle cross-section is shown as pink.
The first Klein Strip shown begins with only a y-line visible at the front and this line disappears as it rotates around to the w-line at the back. At the front the rest of the Klein Strip can't be seen in the 3D slice and the hidden w-line rotates around until it is only visible as the z-line at the back. (*Please see note below).
The second Klein Strip shown also begins with only a y-line visible at the front but this rotates around instead to the z-line at the back. (This infers that it remains at the centre of the Klein Strip in our 3D slice). At the front the rest of the Klein Strip still can't be seen but the hidden w-line this time rotates around to the visible y-line at the back. This time we can see that the back must be a full circle cross-section.
Because of these depictions, I can not see at the moment anymore that it is possible to rotate one in any way to make it look like the other in our 3D slice.
There doesn't seem to be anyway to rotate any invariant planes to achieve that result...
I also have to recognise you Teragon on working out the following toroidal vortex.
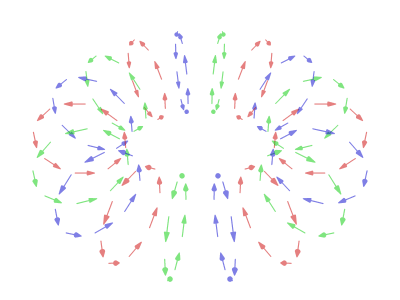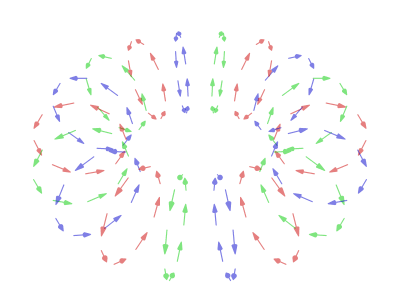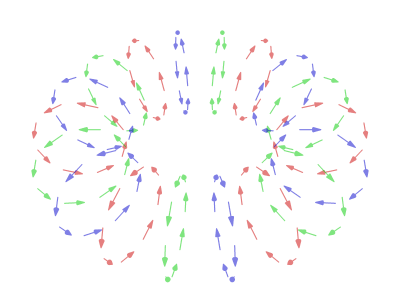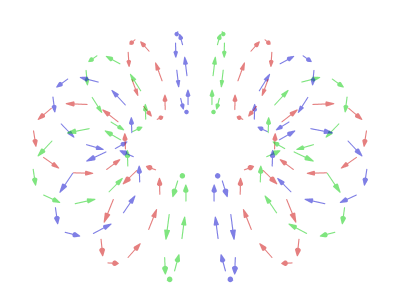
That seems to be exactly the morph that would need to occur to get one shape to transform into another.
I don't now think that it is a normal motion of a solid in 4D unfortunately but you did well to determine that from what I had provided.
That is sad for me in a sense
But out of that I wonder if the two pictures above then represent just 2 of the available ring Klein Strip versions. Hmmm?
Here are images matching these two to what we would see:
 =
= 
 =
= 
A Mobius Strip in our world has two versions: clockwise and anti-clockwise.
Is it possible that a Klein Strip in a 4D world actually has a whole 360° of different Klein Strip versions?
Is that what my animation represents? Does it represent each of the different possible Klein Strips that we can observe (or a 3D slice of)?
What about that Teragon?
* (Just from above) I was interested to notice in the first depiction that the y-line at the front rotates until it is the w-line at the back, and the w-line at the front rotates until it is the z-line at the back. So neither of those form the Mobius strip by themselves. It is the rotations of the circle cross-sections in-between that go to form the Mobius strip that we see. So the total Mobius Strip seen is a series of different angled diametre lines from differently angled circles of which only the diametre line can be seen. Cool hey?


I'll explain these pictures...
They are representing the plane that the Klein Strip ring is lying in as the x,y plane.
We can only see the x/y/z planes in a 3D slice so these are shown darker. The w space is shown as more transparent. The front circle cross-section of the Klein Strip is shown as red and the back circle cross-section is shown as pink.
The first Klein Strip shown begins with only a y-line visible at the front and this line disappears as it rotates around to the w-line at the back. At the front the rest of the Klein Strip can't be seen in the 3D slice and the hidden w-line rotates around until it is only visible as the z-line at the back. (*Please see note below).
The second Klein Strip shown also begins with only a y-line visible at the front but this rotates around instead to the z-line at the back. (This infers that it remains at the centre of the Klein Strip in our 3D slice). At the front the rest of the Klein Strip still can't be seen but the hidden w-line this time rotates around to the visible y-line at the back. This time we can see that the back must be a full circle cross-section.
Because of these depictions, I can not see at the moment anymore that it is possible to rotate one in any way to make it look like the other in our 3D slice.
There doesn't seem to be anyway to rotate any invariant planes to achieve that result...
I also have to recognise you Teragon on working out the following toroidal vortex.

That seems to be exactly the morph that would need to occur to get one shape to transform into another.
I don't now think that it is a normal motion of a solid in 4D unfortunately but you did well to determine that from what I had provided.
That is sad for me in a sense

But out of that I wonder if the two pictures above then represent just 2 of the available ring Klein Strip versions. Hmmm?
Here are images matching these two to what we would see:
 =
= 
 =
= 
A Mobius Strip in our world has two versions: clockwise and anti-clockwise.
Is it possible that a Klein Strip in a 4D world actually has a whole 360° of different Klein Strip versions?
Is that what my animation represents? Does it represent each of the different possible Klein Strips that we can observe (or a 3D slice of)?
What about that Teragon?
* (Just from above) I was interested to notice in the first depiction that the y-line at the front rotates until it is the w-line at the back, and the w-line at the front rotates until it is the z-line at the back. So neither of those form the Mobius strip by themselves. It is the rotations of the circle cross-sections in-between that go to form the Mobius strip that we see. So the total Mobius Strip seen is a series of different angled diametre lines from differently angled circles of which only the diametre line can be seen. Cool hey?
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Traversable Klein 'bottle' paths
I'm sorry for that, gonegahgah.
You've shown exactly what I meant by toroidal rotation. What has baffled me in my recent post was a step further though. As I have looked at the transformation of the object between the front and the back side, it wouldn't fit together with a toroidal rotation.
The animation of the toroidal rotation I presented is a common one and wasn't made by myself in case you think so.
As I understand it, this kind of Moebius band has only one version, because it looks the same in w- and -w-direction. Therefore you can rotate this Moebius band into it's mirror image.
There are always two chiralities possible in any number of dimensions. Imagine an object represented by the directions A B C D, where the object looks different in every direcion (including the negative directions -A -B -C -D).
Takeing a mirror image will always invert a coordinate, for expamle A B C -D. The mirror image is different from the original object, if no rotations can transfer it to itself. (180°-) rotations always exchange the sign of two directions. If you rotate it in BD, you get A -B C D. You can check this for any combination of mirror operations and any number of dimensions, you always get two types of objects.
Edit: You're sort of right too that there are different possibilities to curve this Moebius band in 4D, as I describe them in the last paragraph. Those different orientations are transferable into each other with a toroidal rotation however, but only as long as every direction normal to the loop remains smaller than the radius.
Yeah, but it's a matter of definition if you say "y goes to w and w goes to z", or "y goes to z and w stays at w". The unique feature of the surface is the surface normal vector.
I think the two pictures of your animation represent the two main types to fold a spheritorus Moebius strip in 4D. The first one is a cylindrical extrusion of the 3D Moebius strip and the normal vector rotation (twisting) takes place in the z direction and the plane of the loop. The second one is the version where the twisting takes place only in the plane perpendicular to the plane loop, which means that normal vector never is inclined towards the center of the loop or away from it.
You've shown exactly what I meant by toroidal rotation. What has baffled me in my recent post was a step further though. As I have looked at the transformation of the object between the front and the back side, it wouldn't fit together with a toroidal rotation.
The animation of the toroidal rotation I presented is a common one and wasn't made by myself in case you think so.
gonegahgah wrote:A Mobius Strip in our world has two versions: clockwise and anti-clockwise.
Is it possible that a Klein Strip in a 4D world actually has a whole 360° of different Klein Strip versions?
Is that what my animation represents? Does it represent each of the different possible Klein Strips that we can observe (or a 3D slice of)?
As I understand it, this kind of Moebius band has only one version, because it looks the same in w- and -w-direction. Therefore you can rotate this Moebius band into it's mirror image.
There are always two chiralities possible in any number of dimensions. Imagine an object represented by the directions A B C D, where the object looks different in every direcion (including the negative directions -A -B -C -D).
Takeing a mirror image will always invert a coordinate, for expamle A B C -D. The mirror image is different from the original object, if no rotations can transfer it to itself. (180°-) rotations always exchange the sign of two directions. If you rotate it in BD, you get A -B C D. You can check this for any combination of mirror operations and any number of dimensions, you always get two types of objects.
Edit: You're sort of right too that there are different possibilities to curve this Moebius band in 4D, as I describe them in the last paragraph. Those different orientations are transferable into each other with a toroidal rotation however, but only as long as every direction normal to the loop remains smaller than the radius.
gonegahgah wrote:* (Just from above) I was interested to notice in the first depiction that the y-line at the front rotates until it is the w-line at the back, and the w-line at the front rotates until it is the z-line at the back. So neither of those form the Mobius strip by themselves. It is the rotations of the circle cross-sections in-between that go to form the Mobius strip that we see. So the total Mobius Strip seen is a series of different angled diametre lines from differently angled circles of which only the diametre line can be seen. Cool hey?
Yeah, but it's a matter of definition if you say "y goes to w and w goes to z", or "y goes to z and w stays at w". The unique feature of the surface is the surface normal vector.
I think the two pictures of your animation represent the two main types to fold a spheritorus Moebius strip in 4D. The first one is a cylindrical extrusion of the 3D Moebius strip and the normal vector rotation (twisting) takes place in the z direction and the plane of the loop. The second one is the version where the twisting takes place only in the plane perpendicular to the plane loop, which means that normal vector never is inclined towards the center of the loop or away from it.
Last edited by Teragon on Sat Aug 22, 2015 12:37 pm, edited 1 time in total.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Traversable Klein 'bottle' paths
Teragon wrote:... although I don't know where the morphing effect comes from as the colors represent the distance in the w-direction and I'd expect the w-coordinate to be constant.
That's just an artifact of my stepping the slices. If they were fully overlaid that shouldn't occur.
Teragon wrote:Really don't know what's going on here. I'd like to take a look at the code you used, if that's possible, gonegahgah.
Here are the parametric equations that produce the animation:
x(u,v,t) = (R + r * (sin(v / 2) * sin(u + t) * cos(t) * cos(v / 2 + π/2) + cos(u + t) * cos(v / 2))) * sin(v)
y(u,v,t) = (R + r * (sin(v / 2) * sin(u + t) * cos(t) * cos(v / 2 + π/2) + cos(u + t) * cos(v / 2))) * cos(v)
z(u,v,t) = r * (sin(v / 2) * sin(u + t) * cos(t) * sin(v / 2 + π/2) + cos(u + t) * sin(v / 2))
0 ≤ u ≤ 2π (30 steps), 0 ≤ v ≤ 2π (90 steps), 0 ≤ t ≤ 2π (120 steps)
Teragon wrote:Yeah, but it's a matter of definition if you say "y goes to w and w goes to z", or "y goes to z and w stays at w". The unique feature of the surface is the surface normal vector.
Just clarifying Teragon: (1) Y↔w while W↔z or (2) Y↔z & W↔y - with UPPERCASE at front cross-section and lowercase at back cross-section.
There is always a twist.
Teragon wrote:As I have looked at the transformation of the object between the front and the back side, it wouldn't fit together with a toroidal rotation.
Yes I can see that now. The front would be rotating between W↔Y while the back rotates between w→z→y→w.
One thing I realised (I think) is that you may be able to rotate around one axis even in 4D (the x-axis at the back). Is that possible? But still, it's getting complicated...
Teragon wrote:As I understand it, this kind of Moebius band has only one version, because it looks the same in w- and -w-direction. Therefore you can rotate this Moebius band into it's mirror image.
I'm not sure what you mean Teragon? A clockwise Mobius Band will look like a clockwise Mobius Band when you turn it over. It won't ever look like its mirror image (except perhaps in 4D by rotating it through itself).
There are definitely two types of Mobius Band in our 3D world: clockwise and anti-clockwise.
Teragon wrote:You're sort of right too that there are different possibilities to curve this Moebius band in 4D, as I describe them in the last paragraph. Those different orientations are transferable into each other with a toroidal rotation however, but only as long as every direction normal to the loop remains smaller than the radius.
Cool, I'm glad something is still coming out of all this.
I figure it's possible - in our mind - to rotate the w,y,z-axes together at the back around the x-axis and that represents the different positions where the front W,Y can twist around to; giving a full 360° of possibilities.
Being 4D these might not really have a clockwise/anticlockwise orientation. After all is 'up' able to be distinguished as clockwise or anti-clockwise to both 'left' and 'forward' at once?
I'll draw a picture when I get home if that doesn't make much sense...
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Traversable Klein 'bottle' paths
gonegahgah wrote:Here are the parametric equations that produce the animation:
x(u,v,t) = (R + r * (sin(v / 2) * sin(u + t) * cos(t) * cos(v / 2 + π/2) + cos(u + t) * cos(v / 2))) * sin(v)
y(u,v,t) = (R + r * (sin(v / 2) * sin(u + t) * cos(t) * cos(v / 2 + π/2) + cos(u + t) * cos(v / 2))) * cos(v)
z(u,v,t) = r * (sin(v / 2) * sin(u + t) * cos(t) * sin(v / 2 + π/2) + cos(u + t) * sin(v / 2))
0 ≤ u ≤ 2π (30 steps), 0 ≤ v ≤ 2π (90 steps), 0 ≤ t ≤ 2π (120 steps)
Thank you, I'll have a look at them later.
gonegahgah wrote:One thing I realised (I think) is that you may be able to rotate around one axis even in 4D (the x-axis at the back). Is that possible? But still, it's getting complicated...
A rotation is always around two axes. You can rotate first around xw, then around xz, so every coordinate except for x changes (disregarding the curveture), if that is what you mean.
gonegahgah wrote:Teragon wrote:As I understand it, this kind of Moebius band has only one version, because it looks the same in w- and -w-direction. Therefore you can rotate this Moebius band into it's mirror image.
I'm not sure what you mean Teragon? A clockwise Mobius Band will look like a clockwise Mobius Band when you turn it over. It won't ever look like its mirror image (except perhaps in 4D by rotating it through itself).
There are definitely two types of Mobius Band in our 3D world: clockwise and anti-clockwise.
Yes, but 'm talking about 4D of course.
gonegahgah wrote:I figure it's possible - in our mind - to rotate the w,y,z-axes together at the back around the x-axis and that represents the different positions where the front W,Y can twist around to; giving a full 360° of possibilities.
Being 4D these might not really have a clockwise/anticlockwise orientation. After all is 'up' able to be distinguished as clockwise or anti-clockwise to both 'left' and 'forward' at once?
I'll draw a picture when I get home if that doesn't make much sense...
I think we're talking about the same thing. Still it sounds like you could rotate around a single axis in 4D - you can't. At any location on the loop there is also one direction perpendicular to x that belongs to the center of the rotation. The normal vector pointing in z direction at one place of the loop can either go towards x or towards w or to any angle between the two axes, if the loop goes in y-direction. Going to -x is equivalent to going to x though (just rotate the object by 180° in the xw plane), so there is no chirality in this object. Chiral Moebius bands in 4D involve two loops with a twist. I've alredy made some visualizations about some of these aspects. I'm going to discuss them soon. Hopefully some issues will become clear then.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Traversable Klein 'bottle' paths
Well that sucks. I accidentally lean on the [ctrl] key while typing and my new post disappears changing to quoting the previous post! What's with that? Sigh.
Too much to retype. I'll try again later...
Here's a little bit at least...

This is supposed to show the possibilities for the rear part of the Mobius band (the blue and red circles; the box just shows the axes and the alignments).
It shows:
1. the red diametre of the cross-section at the back aligning with any angle between the w and z axes while,
2. the blue diametre of the cross-section at the back aligning with any angle between the z and y axes while,
3. maintaining 90° to each other.
Does this show that the front Y-line can twist to any of 360° of lines at the rear between the w and z lines while the W-line twists to 360° of lines between the z and y lines at the rear; as long as they remain 90° to each other?
Does that mean there are 360° of varieties of Klein Bands? (And perhaps 2x this as well; but I'll have discuss that next time... Sigh...)


There was also stuff on tumbling, and comparing mirror images to left handed objects, etc, etc...
A picture I drew and discussed but that will have to wait:

Too much to retype. I'll try again later...
Here's a little bit at least...

This is supposed to show the possibilities for the rear part of the Mobius band (the blue and red circles; the box just shows the axes and the alignments).
It shows:
1. the red diametre of the cross-section at the back aligning with any angle between the w and z axes while,
2. the blue diametre of the cross-section at the back aligning with any angle between the z and y axes while,
3. maintaining 90° to each other.
Does this show that the front Y-line can twist to any of 360° of lines at the rear between the w and z lines while the W-line twists to 360° of lines between the z and y lines at the rear; as long as they remain 90° to each other?
Does that mean there are 360° of varieties of Klein Bands? (And perhaps 2x this as well; but I'll have discuss that next time... Sigh...)


There was also stuff on tumbling, and comparing mirror images to left handed objects, etc, etc...
A picture I drew and discussed but that will have to wait:

Last edited by gonegahgah on Mon Aug 24, 2015 9:54 am, edited 2 times in total.
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Traversable Klein 'bottle' paths
Anyhow, I created these paired depictions to some different Klein Strips:
00° =
= 
45° =
= 
90° =
= 
The angle for each of these on the left is the amount the red cross-section diametre line is angled between z and w and the blue cross-section diametre is angled between y and z.
The red Y-line at the front twists around to the red line residing in the plane formed by the z-w axes at the back.
The blue W-line at the front twists around to a blue line residing in the plane formed by the y-z axes at the back.
You can see that these depictions are just taken straight from the 0°, 45° and 90° frames in my Klein Band animation.

It may be that this animation is just a representation of all the simple Klein Band aspects.
One puzzle to this is that, from the pictures on the left, it looked as though only flat bands would be the result.
It took me awhile but I think the solution may be that the wedges that form the path have to bleed through as they twist; and these may form the shapes we see.
The path is actually made of lots of twisting wedges rather than lines (as is also the case in the simplest mathematical depiction of a Mobius Band).
How does that sound, Teragon?
I also thought about how simple shapes, like a cube or sphere, from a 4D direction pass through our world as plane slices but how objects that have 4 dimensions, like a tesseract or glome, pass through our world as solid slices.
Even though a Klein Band is flat in 4D I think it might still be a combination of these occurances because of its twist.
How does that sound too, Teragon?
[But, I'm not sure...] Is the twist enough?
When a 2Der looks at our Mobius Band all they see is a line curving up or down through a straight line that is one cross cut of the Mobius.
They can't even see the ring unless the Mobius Band is on its side.
Maybe all we will see is a ribbon too; although I guess we can at least see the whole ring which the 2Der can't.
Such a fascinating shape a Klein Band. More combinations possibly than I ever realised...
Can it really be as boring as that to look at in a 3D slice of 4D space?
00°
 =
= 
45°
 =
= 
90°
 =
= 
The angle for each of these on the left is the amount the red cross-section diametre line is angled between z and w and the blue cross-section diametre is angled between y and z.
The red Y-line at the front twists around to the red line residing in the plane formed by the z-w axes at the back.
The blue W-line at the front twists around to a blue line residing in the plane formed by the y-z axes at the back.
You can see that these depictions are just taken straight from the 0°, 45° and 90° frames in my Klein Band animation.

It may be that this animation is just a representation of all the simple Klein Band aspects.
One puzzle to this is that, from the pictures on the left, it looked as though only flat bands would be the result.
It took me awhile but I think the solution may be that the wedges that form the path have to bleed through as they twist; and these may form the shapes we see.
The path is actually made of lots of twisting wedges rather than lines (as is also the case in the simplest mathematical depiction of a Mobius Band).
How does that sound, Teragon?
I also thought about how simple shapes, like a cube or sphere, from a 4D direction pass through our world as plane slices but how objects that have 4 dimensions, like a tesseract or glome, pass through our world as solid slices.
Even though a Klein Band is flat in 4D I think it might still be a combination of these occurances because of its twist.
How does that sound too, Teragon?
[But, I'm not sure...] Is the twist enough?
When a 2Der looks at our Mobius Band all they see is a line curving up or down through a straight line that is one cross cut of the Mobius.
They can't even see the ring unless the Mobius Band is on its side.
Maybe all we will see is a ribbon too; although I guess we can at least see the whole ring which the 2Der can't.
Such a fascinating shape a Klein Band. More combinations possibly than I ever realised...
Can it really be as boring as that to look at in a 3D slice of 4D space?
Last edited by gonegahgah on Sun Aug 23, 2015 10:35 am, edited 1 time in total.
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Traversable Klein 'bottle' paths
gonegahgah wrote:Even though a Klein Band is flat in 4D I think it might still be a combination of these occurances because of its twist.
How does that sound too, Teragon?
That's what I was trying to point out. The Moebius band is a 3D shape and therefore has a 2D cross section, except when the normal vector of the surface is also normal to the slice! This is only the case at one point on the Moebius strip, namely the one at the back side. That's why I pointed out to look at the obligue orientations between the two extremes. The animation doesn't show a cross section of the Moebius strip. The structure of a Moebius strip is actually hard to determine with a cross section. Take a 2D cross section of a Moebius strip in 3D and you'll know what I mean.
I think I know now how to interpret the animation. It shows a transition between the different twist directions, as you identified them, but it's a projection onto a 3-plane like the retina of a 4D being! It's a 3D image of a Moebius strip as a 4D being would see it. Altough rarely used this is my favorite form of representation. It would be possible to shade it in a way that it becomes evident what is more close to the observer and what is further apart (I'll do that).
You're right with assessment that there is a range of possible twists in 4D spheritoric Moebius strips. Still I can only repeat myself that these objects do not have a clockwise and counterclockwise orientation. Therefore only 180° of possible twists are left.
I'd also like to question the practice of defining twists of surface tangential vectors.

This is a cross section of a flat torus in 4D (a full 2-torus), the blue and the yellow vector represent the tangential vectors of the surface. Within one revolution, does the yellow vector go to x or does it stay where it is, or does it go to any angle between x and z? It just makes no sense to talk about tangential vectors like that. There is no reference point to define in which direction one distinct vector points at all. It's just how we define them. The only object that matters is the entirety of all tangential vectors - the hyperplane, and a hyperplane is elegantly defined by just one vector - the normal vector of the surface.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Traversable Klein 'bottle' paths
Teragon wrote:I think I know now how to interpret the animation. It shows a transition between the different twist directions, as you identified them, but it's a projection onto a 3-plane like the retina of a 4D being! It's a 3D image of a Moebius strip as a 4D being would see it. Altough rarely used this is my favorite form of representation. It would be possible to shade it in a way that it becomes evident what is more close to the observer and what is further apart (I'll do that).
Thank you Teragon. You give me some hope!
Teragon wrote:You're right with assessment that there is a range of possible twists in 4D spheritoric Moebius strips. Still I can only repeat myself that these objects do not have a clockwise and counterclockwise orientation. Therefore only 180° of possible twists are left.
Hmmm, I'm not 100% convinced of this yet... but give me a chance to explore it further... You might have guessed why I was drawing the clock faces...
I remember now one of the things I wanted to ask you in my previous post that was [ctrl][whatevered] out of existance...
There is a motion they describe in normal space called tumbling (out of control) I think. From what I understand it is where an 3D object is attempting to rotate along two axes at once.
Apparently it is very undesirable in space or in a plane.
I was wondering if the same motion in 4D could leave one axis stationary? Or is that impossible?
Last edited by gonegahgah on Sun Aug 23, 2015 11:03 am, edited 1 time in total.
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Traversable Klein 'bottle' paths
There it is

Green is the mean distance, the more red the closer to us and more blue the further apart (or the other way round). It's easiest to understand if you compare it to a 2D Moebius strip and draw the parallels. A 4D beeing would see the whole object at once of course, including what seems as the interior to us. Aparent asymmetries in the hue come from the natural 3D shading the programm does.
I'm dreaming about an animation where the whole 4D object is parametrized and rotations are made via rotation matrices. The w coordinate is then replaced by a value for the color shading, while the backside is not shown. Even more natural would be defining the shading according to the angle of the surface normal towards a virtual light source. This would be maby the most natural representation of a 4D object since it comes most close to how the process of seeing would work in any number of dimensions. Such a project is beyond my capabilities at the time.

Green is the mean distance, the more red the closer to us and more blue the further apart (or the other way round). It's easiest to understand if you compare it to a 2D Moebius strip and draw the parallels. A 4D beeing would see the whole object at once of course, including what seems as the interior to us. Aparent asymmetries in the hue come from the natural 3D shading the programm does.
I'm dreaming about an animation where the whole 4D object is parametrized and rotations are made via rotation matrices. The w coordinate is then replaced by a value for the color shading, while the backside is not shown. Even more natural would be defining the shading according to the angle of the surface normal towards a virtual light source. This would be maby the most natural representation of a 4D object since it comes most close to how the process of seeing would work in any number of dimensions. Such a project is beyond my capabilities at the time.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Traversable Klein 'bottle' paths
That is awesome Teragon!
I was starting wonder and think that it might be possible to work out the 4D parameters hopefully because of these new depictions that I made. They hopefully provide information I didn't have before...
You would still have one parameter for stepping around the main circle (v), one for stepping around each cross section circumference (u), and an extra one for stepping the angle from w→z while z→y (maybe q).



Instead of a 2D mesh we are then hoping for a 3D mesh (ie. made of trapezoidal prisms, trapezoidal trapeziums, whatever they ares).
What is a six flat sided solid called where all the faces can be irregular?
I hadn't thought of making the 'W' direction be colour in the parameters. That's despite using it in the rotation into the vertical animation which just seemed like a good idea. That could be very good.
Though transparency also comes in handy. I would like to have the current 3D slice solid so that the player knows what they can interact with.
I would also like to be able to depict greater bulk as more opaqueness as a guide to the player too. I'll be interested to investigate what it would look like using my rotational projection as well.
Very interesting!
So, is the red part learning towards us while the blue part leans away (just trying to relate the Mobius Strip)?
Why is it a pinched torus? Would the following parameters be better (these give the distinctive tilt; should that not be there)?
x(u,v) = (R + r * (sin(v / 2) * sin(u) * cos(v / 2 + π / 2) + cos(u) * cos(v / 2))) * sin(v)
y(u,v) = (R + r * (sin(v / 2) * sin(u) * cos(v / 2 + π / 2) + cos(u) * cos(v / 2))) * cos(v)
z(u,v) = r * (sin(v / 2) * sin(u) * sin(v / 2 + π / 2) + cos(u) * sin(v / 2))
I'm getting this thought that the different Klein Strip orientations might make for some interesting computer puzzle game mechanics...
Teragon wrote:I'm dreaming about an animation where the whole 4D object is parametrized and rotations are made via rotation matrices. The w coordinate is then replaced by a value for the color shading, while the backside is not shown. Even more natural would be defining the shading according to the angle of the surface normal towards a virtual light source. This would be maby the most natural representation of a 4D object since it comes most close to how the process of seeing would work in any number of dimensions. Such a project is beyond my capabilities at the time.
I was starting wonder and think that it might be possible to work out the 4D parameters hopefully because of these new depictions that I made. They hopefully provide information I didn't have before...
You would still have one parameter for stepping around the main circle (v), one for stepping around each cross section circumference (u), and an extra one for stepping the angle from w→z while z→y (maybe q).



Instead of a 2D mesh we are then hoping for a 3D mesh (ie. made of trapezoidal prisms, trapezoidal trapeziums, whatever they ares).
What is a six flat sided solid called where all the faces can be irregular?
I hadn't thought of making the 'W' direction be colour in the parameters. That's despite using it in the rotation into the vertical animation which just seemed like a good idea. That could be very good.
Though transparency also comes in handy. I would like to have the current 3D slice solid so that the player knows what they can interact with.
I would also like to be able to depict greater bulk as more opaqueness as a guide to the player too. I'll be interested to investigate what it would look like using my rotational projection as well.
Teragon wrote:Even more natural would be defining the shading according to the angle of the surface normal towards a virtual light source. This would be maby the most natural representation of a 4D object since it comes most close to how the process of seeing would work in any number of dimensions.
Very interesting!

Teragon wrote:Green is the mean distance, the more red the closer to us and more blue the further apart (or the other way round). It's easiest to understand if you compare it to a 2D Moebius strip and draw the parallels.
So, is the red part learning towards us while the blue part leans away (just trying to relate the Mobius Strip)?
Why is it a pinched torus? Would the following parameters be better (these give the distinctive tilt; should that not be there)?
x(u,v) = (R + r * (sin(v / 2) * sin(u) * cos(v / 2 + π / 2) + cos(u) * cos(v / 2))) * sin(v)
y(u,v) = (R + r * (sin(v / 2) * sin(u) * cos(v / 2 + π / 2) + cos(u) * cos(v / 2))) * cos(v)
z(u,v) = r * (sin(v / 2) * sin(u) * sin(v / 2 + π / 2) + cos(u) * sin(v / 2))
Teragon wrote:I'm dreaming about...
I'm getting this thought that the different Klein Strip orientations might make for some interesting computer puzzle game mechanics...
Last edited by gonegahgah on Sun Aug 23, 2015 11:55 am, edited 1 time in total.
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Traversable Klein 'bottle' paths
gonegahgah wrote:Hmmm, I'm not 100% convinced of this yet... but give me a chance to explore it further... You might have guessed why I was drawing the clock faces...
Let me take up your example with the clock. A 4D clock may be described by four coordinates: +x pointing in "3-direction", +z pointing in "12-direction", +y pointing out of the front side of the clock and +w pointing at the ana side of the clock. Plus we suppose xyz plane is a mirror plane of the clock. Now we make a mirror image of the clock with respect to the plane xzw as shown in your figure. Everything is the same except that the front and back side of the clock are exchanged with the face pointing in -y direction. Now we make a turn around the xz-plane of the clock, leaving the the 3 and the 12 where they are. The front side goes to +y again, while ana goes to kata. Since ana and kata are the same, the mirror image of this object is topologically ident to the original object.
gonegahgah wrote:I remember now one of the things I wanted to ask you in my previous post that was [ctrl][whatevered] out of existance...
There is a motion they describe in normal space called tumbling (out of control) I think. From what I understand it is where an 3D object is attempting to rotate along two axes at once.
Apparently it is very undesirable in space or in a plane.
I was wondering if the same motion in 4D could leave one axis stationary? Or is that impossible?
For a rotating body I don't now. But as a twist of strip it's possible as long as the surface ends up flipped by 180° after one loop. I wonder, when you form a 4D Moebius strip by twisting a 3D paper strip and glueing both ends together, if there is a most stable configuration the strip wants to take up or if every twisting direction takes the same amaount of bending energy.
gonegahgah wrote:What is a six flat sided solid called where all the faces can be irregular?
Irregular hexahedron maby.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Traversable Klein 'bottle' paths
Teragon wrote:Irregular hexahedron maby.
Excellent, that checks out. Thank you

Teragon wrote:I wonder, when you form a 4D Moebius strip by twisting a 3D paper strip and glueing both ends together, if there is a most stable configuration the strip wants to take up or if every twisting direction takes the same amaount of bending energy.
Probably only due to the paper itself wanting to retain its flat square shape as much as possible so the twist might always be a bit more squeezed.
Certainly it is not the edge length that is the worry because there is only one edge. It might be possible to cut a curving strip from paper that sits more evenly.
I know you would have to make special cuts of flat paper to try to recreate the depiction that I made originally of the filled Klein Band... I tried with straight edged pieces and that didn't work...
Teragon wrote:Let me take up your example with the clock. A 4D clock may be described by four coordinates: +x pointing in "3-direction", +z pointing in "12-direction", +y pointing out of the front side of the clock and +w pointing at the ana side of the clock. Plus we suppose xyz plane is a mirror plane of the clock. Now we make a mirror image of the clock with respect to the plane xzw as shown in your figure. Everything is the same except that the front and back side of the clock are exchanged with the face pointing in -y direction. Now we make a turn around the xz-plane of the clock, leaving the the 3 and the 12 where they are. The front side goes to +y again, while ana goes to kata. Since ana and kata are the same, the mirror image of this object is topologically ident to the original object.
Thanks Teragon I'll study this soon, along with my depictions, to more fully understand.
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Traversable Klein 'bottle' paths
Here's a depiction showing 5 cross sections at 0°, 45°, 90°, 135° and 180° of the simplest (to us) form of Klein Band.

The 3D slices shown are stepped. They are shown as purple through to red to highlight each slice. In total across they represent and are equal to the small radius of any cross section.
Most of the action occurs along the x,y so I can get away with that.
You could consider our slice to be the middle yellow one (though you could side-step into any of course).
The only part visible to us then, in our slice, is the middle of any yellow.
If you look closely this yellow line starts flat on the ground at the front in the y-direction.
Slowely it rotates (as the Klein Strip rotates) in an anti-clockwise direction into being vertical at the back...
If you continued the cross-sections around to the front it would again be flat but underneath.
The cross-sections are actually rotating while they twist - though you can't see it in this depiction.
So the diametre corresponding to the flat yellow line at the front ends up being across all the slices by 180°.
Its perpendicular diametre starts off across all the slices but is vertical and corresponding to the yellow line by the 180° point.
That helps me understand you depiction easier Teragon.

The blue is more in the ana direction and the red is more in the kata direction.
Though it would be nice to see it in the shape I created and not the pinched torus...

The 3D slices shown are stepped. They are shown as purple through to red to highlight each slice. In total across they represent and are equal to the small radius of any cross section.
Most of the action occurs along the x,y so I can get away with that.
You could consider our slice to be the middle yellow one (though you could side-step into any of course).
The only part visible to us then, in our slice, is the middle of any yellow.
If you look closely this yellow line starts flat on the ground at the front in the y-direction.
Slowely it rotates (as the Klein Strip rotates) in an anti-clockwise direction into being vertical at the back...
If you continued the cross-sections around to the front it would again be flat but underneath.
The cross-sections are actually rotating while they twist - though you can't see it in this depiction.
So the diametre corresponding to the flat yellow line at the front ends up being across all the slices by 180°.
Its perpendicular diametre starts off across all the slices but is vertical and corresponding to the yellow line by the 180° point.
That helps me understand you depiction easier Teragon.

The blue is more in the ana direction and the red is more in the kata direction.
Though it would be nice to see it in the shape I created and not the pinched torus...

- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Traversable Klein 'bottle' paths
gonegahgah wrote:The blue is more in the ana direction and the red is more in the kata direction.
Though it would be nice to see it in the shape I created and not the pinched torus...
Now that I've looked at it more closely I think it's showing some hybrid twist. At the front side the normal vector points up, going somewhere between inside and ana, like a 45°-strip, but then turning fully in w-direction. The pinched torus is a more simple version of the Moebius strip where the twist lies wholey outside the loop plane. Let's call it 90°-orientation - the angle representing the minimum angle to the plane of the loop. Unfourtunatly I can't do the color shading for your shape in reasonable time, because the inherent twist makes it much harder to give it a proper shading.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Traversable Klein 'bottle' paths
During my exploration of different Moebius strips and Klein bottles in 4 and higher dimensions, the question arouses how to name the individual shapes in a consistent and suggestive way. I came to the realization that Moebius band may all be considered sections of objects of the dimensionality the space the Moebius strip lives in. It seemed a neat way to call Moebius strips after the shape they were created from with the prefix "Moebius". Every so defined type of Meobius strip has its subspecies, as there are many ways to cut the same shape to obtain different Moebius strips.
As every object I explored is a theme in itself (as any 4D object for a common 3D beeing) I'm going to discuss them not side by side, but one after another. I'm going to give a short describtion of every object at the beginning in the following form:
Short name:
Contains:
- The phrase "Moebius"
- The name of the object the strip is derived from (dropping the prefix "full" in order to get a more compact name)
Full name:
As there are multiple ways to twist a band to a Moebius strip there are different subspecies of Moebius strips. For each loop where a twist can take place, any number (n+1/2) of full twists within one revolution around the loop leads to a Moebius strip. Some Moebius strips may also be twisted in different angles or have a lefthanded and a righthanded version (the latter one is not accounted for in the full name for now). The full name of the Moebius strip comprises the following:
- The number of twists in direction a, b, c... (from the outermost to the innermost loop), 1 standing for one half twist, 2 for three halfs and so on
- The phrase "Moebius"
- The name of the object the strip is derived from (dropping the prefix "full")
- The minimal angle of the surface normal to the plane of the loop
I don't know if the nomenclature is sufficient or even convenient in 5, 6 or higher dimensions as there are many more possibilities there.
Family:
Some Moebius strips may be transferred into each other by deforming them and/or moving parts of the surface through each other. Two such objects are called topologically ident. Tearing, glueing and eliminating loops is not allowed. Based on this definition I'm going to classify Moebius strips into different families, but while Moebius strips with different numbers of twists are topologically different, the number of twists plays no role in this classification. I'm no topologist, so there may be uncertainties as well.
Creation from higher dimensional objects:
How to obtain the object as a twisted section. Should already be evident from the name.
Creation from lower dimensional objects:
How to obtain the object by extrusion of a lower dimensional object and joining both ends together.
Cross sections:
Shape of the cross sections from the Moebius strip that are obtained when a section is done perpendicular to the one or another loop plane.
Number of open directions:
Open directions are directions on a surface where one would leave the surface if one travelled along it. Every Moebius band has at least one open direction. Otherwise it is closed and intersects itself and I'm calling it a Klein bottle.
Number of closed directions:
Closed directions are directions on a surface where one would end up where one started from, if one travelled along them.
Number of twisted directions:
Twisted directions are closed directions on a surface where one would end up on the opposite side of the surface if one travelled one time around the loop.
Chirality:
An object that is chiral has two topologically different versions. In 3D we would talk about a lefthanded and a righthanded version. If an object occupies only a lower dimensional subspace of the space it lives in it's always achiral.
Enough for today. I'm going to start with the common Moebius strip in 3D in the next days, so the concepts I'm using become more clear and dimensional analogy is applicable later on.
If there are any questions, ideas, criticism, feel free to share your thoughts.
As every object I explored is a theme in itself (as any 4D object for a common 3D beeing) I'm going to discuss them not side by side, but one after another. I'm going to give a short describtion of every object at the beginning in the following form:
Short name:
Contains:
- The phrase "Moebius"
- The name of the object the strip is derived from (dropping the prefix "full" in order to get a more compact name)
Full name:
As there are multiple ways to twist a band to a Moebius strip there are different subspecies of Moebius strips. For each loop where a twist can take place, any number (n+1/2) of full twists within one revolution around the loop leads to a Moebius strip. Some Moebius strips may also be twisted in different angles or have a lefthanded and a righthanded version (the latter one is not accounted for in the full name for now). The full name of the Moebius strip comprises the following:
- The number of twists in direction a, b, c... (from the outermost to the innermost loop), 1 standing for one half twist, 2 for three halfs and so on
- The phrase "Moebius"
- The name of the object the strip is derived from (dropping the prefix "full")
- The minimal angle of the surface normal to the plane of the loop
I don't know if the nomenclature is sufficient or even convenient in 5, 6 or higher dimensions as there are many more possibilities there.
Family:
Some Moebius strips may be transferred into each other by deforming them and/or moving parts of the surface through each other. Two such objects are called topologically ident. Tearing, glueing and eliminating loops is not allowed. Based on this definition I'm going to classify Moebius strips into different families, but while Moebius strips with different numbers of twists are topologically different, the number of twists plays no role in this classification. I'm no topologist, so there may be uncertainties as well.
Creation from higher dimensional objects:
How to obtain the object as a twisted section. Should already be evident from the name.
Creation from lower dimensional objects:
How to obtain the object by extrusion of a lower dimensional object and joining both ends together.
Cross sections:
Shape of the cross sections from the Moebius strip that are obtained when a section is done perpendicular to the one or another loop plane.
Number of open directions:
Open directions are directions on a surface where one would leave the surface if one travelled along it. Every Moebius band has at least one open direction. Otherwise it is closed and intersects itself and I'm calling it a Klein bottle.
Number of closed directions:
Closed directions are directions on a surface where one would end up where one started from, if one travelled along them.
Number of twisted directions:
Twisted directions are closed directions on a surface where one would end up on the opposite side of the surface if one travelled one time around the loop.
Chirality:
An object that is chiral has two topologically different versions. In 3D we would talk about a lefthanded and a righthanded version. If an object occupies only a lower dimensional subspace of the space it lives in it's always achiral.
Enough for today. I'm going to start with the common Moebius strip in 3D in the next days, so the concepts I'm using become more clear and dimensional analogy is applicable later on.
If there are any questions, ideas, criticism, feel free to share your thoughts.
Last edited by Teragon on Wed Sep 02, 2015 8:31 pm, edited 1 time in total.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Traversable Klein 'bottle' paths
That's cool Teragon.
I'm just working out the 4D parametric equations for the 'simple' Klein Band varieties. So far I have:
w = r * (cos(V / 2) * cos(V / 2) * cos(u + V / 2) + sin(V / 2) * sin(t) * sin(t) * cos(u + V / 2))
x = R * sin(V)
y = (R + r * (cos(V / 2) * cos(V / 2) * sin(u + V / 2) + sin(V / 2) * cos(t) * cos(t) * sin(u + V / 2))) * cos(V)
z = r * ...
The t value lets you rotate between the different variations of the 4D basic Klein strip.
I didn't realise how late it is. After midnight. I'll try to finish it off tomorrow morning...
Hopefully the above are on the right track.
The only problem seems to be that they produce an object outline mesh which means that despite some of the bulk being in our 3D slice little of it would be rendered!
I would also need some way to get the current 3D slice cross-section of the 4D object...
I've seen how 3D modelling programs do cross-sectional slices for 3D objects so it must be possible to do similar for 4D objects?
I'm just working out the 4D parametric equations for the 'simple' Klein Band varieties. So far I have:
w = r * (cos(V / 2) * cos(V / 2) * cos(u + V / 2) + sin(V / 2) * sin(t) * sin(t) * cos(u + V / 2))
x = R * sin(V)
y = (R + r * (cos(V / 2) * cos(V / 2) * sin(u + V / 2) + sin(V / 2) * cos(t) * cos(t) * sin(u + V / 2))) * cos(V)
z = r * ...
The t value lets you rotate between the different variations of the 4D basic Klein strip.
I didn't realise how late it is. After midnight. I'll try to finish it off tomorrow morning...
Hopefully the above are on the right track.
The only problem seems to be that they produce an object outline mesh which means that despite some of the bulk being in our 3D slice little of it would be rendered!
I would also need some way to get the current 3D slice cross-section of the 4D object...
I've seen how 3D modelling programs do cross-sectional slices for 3D objects so it must be possible to do similar for 4D objects?
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Traversable Klein 'bottle' paths
That's the difficulty with 4D objects. They're described by 3 parameters, but common visualization packages allow for 2 of them. I guess it would be quite different to map the 3 parameters to the 2 that are relevant in the 3D slice. Another drawback is that it's not an efficient form of programming to create every object and every rotation by hand.
I'm not familiar with the software you use. I wonder if it would be economical to calculate the points of the object on one's own:
1.) Vary the parameters of the 3-surface in 3 loops to generate a list of a certain amount of points. A problem may be that a much bigger number of points is necessairy to describe a 4D object than a 3D object.
2.) Choose a rotational plane and rotate the points by multiplication with the associated matrix.
3.) Plot the points as a cross section (just the points where w is in the vicinity of a certain number) or projection (translate the distance w to a scale factor) with a 3D list plot function.
4.) Vary the angle and/or plane of the cross section by hand or increase t automatically and repeat steps 2.) and 4.).
Anyway, that's the wrong topic for this discussion and such questions have probably been discussed in the programming section.
I'm not familiar with the software you use. I wonder if it would be economical to calculate the points of the object on one's own:
1.) Vary the parameters of the 3-surface in 3 loops to generate a list of a certain amount of points. A problem may be that a much bigger number of points is necessairy to describe a 4D object than a 3D object.
2.) Choose a rotational plane and rotate the points by multiplication with the associated matrix.
3.) Plot the points as a cross section (just the points where w is in the vicinity of a certain number) or projection (translate the distance w to a scale factor) with a 3D list plot function.
4.) Vary the angle and/or plane of the cross section by hand or increase t automatically and repeat steps 2.) and 4.).
Anyway, that's the wrong topic for this discussion and such questions have probably been discussed in the programming section.
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Traversable Klein 'bottle' paths
I realised that the following is the twist I am trying to achieve (as in the gold circle in this image)...

The blue axis rotates around in the blue plane as the red axis rotates around in the red plane.
The golden circle cross section doesn't do an ordinary rotation.
It doesn't even do two ordinary rotations.
It does a rotation while it is rotating...
You can do one ordinary rotation but the other needs to be in the newly rotated plane; not one of the w, x, y or z planes... [Edit: Or perhaps not as that will still throw the result off]
Otherwise it produces inaccurate results.
I haven't really seen any formulas for such a rotation. Are there any such things?
Maybe it requires working out the rotation angles for all of the 3-planes involved? Is that possible?
[Edit: Ah so it is as you said Teragon, the twist is what exposes the shape that we see in our 3D slice. Now I see.]

The blue axis rotates around in the blue plane as the red axis rotates around in the red plane.
The golden circle cross section doesn't do an ordinary rotation.
It doesn't even do two ordinary rotations.
It does a rotation while it is rotating...
You can do one ordinary rotation but the other needs to be in the newly rotated plane; not one of the w, x, y or z planes... [Edit: Or perhaps not as that will still throw the result off]
Otherwise it produces inaccurate results.
I haven't really seen any formulas for such a rotation. Are there any such things?
Maybe it requires working out the rotation angles for all of the 3-planes involved? Is that possible?
[Edit: Ah so it is as you said Teragon, the twist is what exposes the shape that we see in our 3D slice. Now I see.]
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Re: Traversable Klein 'bottle' paths
Teragon wrote:That's the difficulty with 4D objects. They're described by 3 parameters, but common visualization packages allow for 2 of them. I guess it would be quite different to map the 3 parameters to the 2 that are relevant in the 3D slice. Another drawback is that it's not an efficient form of programming to create every object and every rotation by hand.
That's why I'm interested in the implicit form of equation for the 4D mobius object. Using it, I can input a hard-coded rotate function that turns and slides it however we want. It's very efficient and easy to use, without a lot of setup time.
It is by will alone, I set my donuts in motion
- ICN5D
- Pentonian
- Posts: 1135
- Joined: Mon Jul 28, 2008 4:25 am
- Location: the Land of Flowers
Re: Traversable Klein 'bottle' paths
gonegahgah, as I said, this is just a normal rotation around an obligue axis. Two rotations combined give another rotation around a different axis. There is only one rotational axis at a time in 3D. Are you familiar with matrix calculus?
ICN5D, which form do you mean by 'implicit form'? Is there a topic where I can look up how you do it?
ICN5D, which form do you mean by 'implicit form'? Is there a topic where I can look up how you do it?
What is deep in our world is superficial in higher dimensions.
- Teragon
- Trionian
- Posts: 137
- Joined: Wed Jul 29, 2015 1:12 pm
Re: Traversable Klein 'bottle' paths
That will be cool ICN5D. I'll try to work it out. [Edit] Well... looking at implicit equations; I'll probably work out parametric equations. How do you make use of implicit equations in programming?
It's kind of like a sale where you take 20% off and then 10%. It's not quite the same as taking 30% off. I'll draw some depictions when I get home...
[Edit]I've seen the matrix stuff in passing but I haven't stopped to work it out. So there's 3 ways to do things!
Teragon wrote:gonegahgah, as I said, this is just a normal rotation around an obligue axis. Two rotations combined give another rotation around a different axis. There is only one rotational axis at a time in 3D. Are you familiar with matrix calculus?
It's kind of like a sale where you take 20% off and then 10%. It's not quite the same as taking 30% off. I'll draw some depictions when I get home...
[Edit]I've seen the matrix stuff in passing but I haven't stopped to work it out. So there's 3 ways to do things!
- gonegahgah
- Tetronian
- Posts: 546
- Joined: Sat Nov 05, 2011 3:27 pm
- Location: Queensland, Australia
Return to Higher Spatial Dimensions
Who is online
Users browsing this forum: No registered users and 41 guests
