Construction of BT-polytopes via partial Stott-expansion

[student91]

I think I can say for most of the BT-polytopes how they can be constructed by partiall Stott-expansion:

Castellated Rhombicosidodecahedral Prism:
This one can be constructed from the 600-cell, in .5.3.-orientation:
o5o3o||o5o3x||x5o3o||o5o3f||o5x3o||o5o3f||x5o3o||o5o3x||o5o3x
the id can be written as f5(-x)3x, which gives a f2x-rectangle. the f-ikes give two f-edges, connected with an x-edge, giving an o2f(2x)-rectangle. The dodecahedra give a x2o(2f)-rectangle, completing into a ike: fox2xfo2oxf&#zx =ike. This ike can get expanded to make a bilbiro. this gives us:
o5o3x || o5x3o || x5o3x || o5o3F || (o5x3o=>f5(-x)3x=>f5o3((-x)+x)=f5o3o || o5o3F || x5o3x || o5x3o || o5o3x. when you diminish the top and bottom parts, you get the castellated rhombicosidodecahedral prism.

Castellated x5x3x-prism:
This can be constructed from the rectified 600-cell, in .5.3.-orientation as well:
......||x5x3o||o5x3f||(f5o3x+o5o3V)||o5x3f||x5x3o||......
expansion: x5x3x ||o5x3F ||(f5o3x=>f5x3((-x)+x)=f5x3o +o5o3(2f+x) ) ||o5x3F||x5x3x =Castellated x5x3x-prism

Thawro-ing, as well as bilbiro-ing, can be seen as such an expansion as well
Thawro-ing: this is a .5.3.-expansion on the right node. e.g. D4.7: this can be constructed form the 600-cell: o5o3o=>o5o3x || o5o3x=> o5x3(-x)=> o5x3o || x5o3x =>x5o3x || o5o3f=>o5o3F || o5x3o=>o5x3x || etc. The difference from the castellated prism is how the middle id is treated.
D4.5.1: can be constructed from rox: ....||x3o5x=>(-x)3x5x=>o3x5x || F3o5o=>(f+2x)3o5o || o3f5o=>x3f5o || f3o5x=> F3o5x || o3x5x=>x3x5x ||.....

Now Bilbiro-ing (this is where I think it gets interesting) let's take D4.6, the one we had difficulty computing it's coordinates: it's made from x3x3o5o:
x3o5o||u3o5o||x3x5o||u3o5x||F3o5o||x3o5u||o3f5x||A3o5o||f3o5u||B3o5x||o3x5u||B3x5o||o3u5x||f3u5o||C3o5o||x3x5f||(reverse order ftw)[A=F+f=2f+1; B=2f; C=3f]
expansion: x3o5x || u3o5x || x3x5x || u3f5o || F3o5x || x3o5(3) || o3B5o ||A3o5x || f3o5(3) ||B3f5o || o3x5(3) || B3x5x || o3(2F)5o || f3u5x|| C3o5x || x3x5F || (reverse order ftw)
The middle part gives C3o5x, which sows how the insertion of that was way less artificial than we thought.

bilbiro-ing of o5o3x3o is made of o5o3o3x, that of o5x3o3o probably from o5o3x3o, though I'm not sure.

Furtermore D4.11 has been showed to be a partiall stott-expansion of ex in a demitesseractic symmetry.
My point is that almost all BT-polytopes we've found so far can be made by partial stott-expansion.
So what we can do next is investigate all possible partial Stott-expansions, determine when they are convex, write a paper, be awesome and eat a cookie (long term goal)

[quickfur]

Yeah, this is my suspicion as well. So Keiji was right after all -- all these CRFebruary polychora actually belong to the same class (though I would expand the category to include those polychora that don't immediately have J91/J92 cells -- it's not so much the surface elements that matter, but the underlying constructions that in many cases allow J91/J92 cells, though not necessarily in all cases). They are all partial (or modified) Stott expansions of the 120-cell family uniforms. In other words, the 4D analogues of J91 and J92.

So then this leads to the next question: are there any crown jewels outside this class?

[Klitzing]

So what we can do next is investigate all possible partial Stott-expansions, determine when they are convex, write a paper, be awesome and eat a cookie (long term goal)

Even so Stott expansion is known since Alicia's paper now for more than 1 century, and my term of "partial Stott expansion" would be quite suggestive (as it should, by choice), the idea of application to a subsymmetry only to my knowledge seems quite new as such, being brought up first here in my webpage, and so far never was published elsewhere, esp. not in a paper. So I think we should at least include that part as well into it somehow ...
--- rk

[quickfur]

This is exciting! So we should write a joint paper together, describing our findings?

I'm thinking the subject of the paper can be partial (or modified) Stott expansion itself, and the CRFs we discovered would serve as examples of the process, so we are not obligated to enumerate all possibilities (which I think will take a lot more work -- and I mean a lot more, given how many possible combinations there are). This way, we can just use our current discoveries (maybe plus some others we might find on the way) as the source data to draw from, which should reduce the total amount of work that needs to be done. Plus, it should keep the paper within reasonable length so that people will actually read it. The idea of partial expansion or modified expansion (e.g., ike -> bilbiro) seems like a good unifying concept for the paper to focus on.

[Marek14]

This is exciting! So we should write a joint paper together, describing our findings?

I'm thinking the subject of the paper can be partial (or modified) Stott expansion itself, and the CRFs we discovered would serve as examples of the process, so we are not obligated to enumerate all possibilities (which I think will take a lot more work -- and I mean a lot more, given how many possible combinations there are). This way, we can just use our current discoveries (maybe plus some others we might find on the way) as the source data to draw from, which should reduce the total amount of work that needs to be done. Plus, it should keep the paper within reasonable length so that people will actually read it. The idea of partial expansion or modified expansion (e.g., ike -> bilbiro) seems like a good unifying concept for the paper to focus on.

It sounds exciting

[student91]

I'm thinking the subject of the paper can be partial (or modified) Stott expansion itself, and the CRFs we discovered would serve as examples of the process, so we are not obligated to enumerate all possibilities (which I think will take a lot more work -- and I mean a lot more, given how many possible combinations there are)

I think the number of combinations is much less than we think. First of all, we "only" have to check all subsymmetries for all polytopes with ikes. (that's not completely true, you also have the case of id being treated differently.) furthermore I think investigations will show we can ignore even more expansions.

This way, we can just use our current discoveries (maybe plus some others we might find on the way) as the source data to draw from, which should reduce the total amount of work that needs to be done. Plus, it should keep the paper within reasonable length so that people will actually read it. The idea of partial expansion or modified expansion (e.g., ike -> bilbiro) seems like a good unifying concept for the paper to focus on.

Maybe we can write two papers, one about partial Stott-expansion, and one about the number of partial Stott-expansions. Anyway, let's investigate those partial Stott-expansions a bit further before we actually write the paper.

[student91]

[...]They are all partial (or modified) Stott expansions of the 120-cell family uniforms. In other words, the 4D analogues of J91 and J92.

Just forgot to tell you, very few of the BT-polytopes are true partial expansions, most of them are built up from parts of expansions and parts of normal uniforms, or had some cutting after the expansion. So I wanted to say: those "pure" forms are probably low in number, with an awful lot of cutting possible.

So then this leads to the next question: are there any crown jewels outside this class?

Apart from the "snubdis antiprism" and the ursachora, very few fall out of this class. Maybe special ones of this class can be seen as crown jewels, the same way the snubdis antiprism is a special one among the segmentochora. I don't think that indexing is very important though. Anyway I think the 2/6-lune might classify as crown jewel, and maybe thawrorh as well.

[quickfur]

Hmm. So this still begs the question, what is it about these BT polychora that makes it possible to incorporate various different surface patches (from different uniforms) into a single CRF? I mean, we don't see as many combinations with, say, the tesseract family. I don't know of that many CRFs that are made from surfaces patches of very different tesseract family uniforms. Partial Stott expansion does apply to quite a few tesseract family uniforms, but you don't see the kind of hybrid cross-attachment of surface patches of divergent derivations closing up, like in the 120-cell family. Why is the 120-cell family so special?

I'm still wondering about my phi-based grid idea. Perhaps it's not so much a grid, as a kind of lattice algebra that takes advantage of the properties of phi, to generate a large number of CRF possibilities. If we can find the underlying thing that generates these possibilities, that's definitely worth a paper in itself, I think.

As for the number of BT polychora: it's true that the "true" partial Stott expansions probably are limited in number, but the number of CRFs derivable from them undergo combinatorial explosion. Take the J92 rhombochoron, for example. It has 4 sites of possible augmentation with thawro's. But that's only the beginning: the augmented J92 rhombochoron now can have other vertices, that previously cannot be deleted in a CRF way, now become diminishable. So each of these rhombochoron augmentations now give birth to their own little litter of other CRFs, now with a mixture of J91's and other cells thrown in. Then those in turn may have more diminishings and augmentations that lead to more shapes. By the time you construct them all, you get quite a large number of CRFs just from the J92 rhombochoron alone. Now some of the bigger bilbiro'ings and thawro'ings inherit a large number of augmentations/diminishings from the parent uniform. Each of those may lead to more augmentations and diminishings. Then you have the various oblique cuttings and lunae, etc. So it undergoes combinatorial explosion to a huge number of distinct CRFs. I wouldn't be surprised if the final number is in the ten thousands or hundred thousands, or perhaps in the hundred millions, like the 600-cell diminishings or the 10,10-duoprism augmentations.

[quickfur]

Anyway, back to the prospective paper on partial expansions: I think it's worthwhile to also include the 3D cases of modified Stott expansion we found: ike -> J91, ike -> J92, ike -> J32. AFAIK, these derivations are entirely new, and have never been considered before, especially the fact that J91 and J92 have direct derivations from ike: they are more than just some slice of the icosidodecahedron with random CRF bits closing it up; these "random bits" turn out to have direct correspondence with the faceted ike from which the rest of the shape is derived.

(But I could be wrong about this being new -- I'm not as well-read as I'd like to be. Klitzing should know, though. )

[student91]

Anyway, back to the prospective paper on partial expansions: I think it's worthwhile to also include the 3D cases of modified Stott expansion we found: ike -> J91, ike -> J92, ike -> J32. AFAIK, these derivations are entirely new, and have never been considered before, especially the fact that J91 and J92 have direct derivations from ike: they are more than just some slice of the icosidodecahedron with random CRF bits closing it up; these "random bits" turn out to have direct correspondence with the faceted ike from which the rest of the shape is derived.

I think we definitely have to include those, they are very important in the partial expansions. We might also want to include ike-pyramid => bilbiro pseudopyramid, ike-pyramid=> thawro pseudopyramid and ike-pyramid=> pocuro pseudopyramid, for a intuitive understanding of what happens before we go to the big things. furthermore, I think 3D-examples are the most useful for explanation, as most readers probably have difficulty visualizing 4D.

(But I could be wrong about this being new -- I'm not as well-read as I'd like to be. Klitzing should know, though. )

I've got that problem too, mostly because I'm restricting myself to free sources. anyway, I've found Stott's paper on a free site:http://www.dwc.knaw.nl/DL/publications/PU00011492.pdf It helped me to understand what Stott-expansions actually are. Basically her expansions take the "limits" of a polytope, those are cells, faces or edges, and move these outside along the line connecting the middle of this "limit" to the center. here's a picture of x6o changing in x6x:

x6o to x6x.png (38.59 KiB) Viewed 142095 times

you can see the "limits" here are edges. those edges are moving parallel to the mirrors that are part of the kaleidoscope (the lines in the picture). In general the limits always move parallel to the intersection of the mirrors whose nodes aren't changed.
Now let's use a subsymmetry, e.g. .3. x6x in .3.-symmetry is Ax3xA&#zx.(A=something) When we expand this, we get (A+x)u3xA. I've made a picture for that as well:

x6x(.3.) normal.png (44.85 KiB) Viewed 142095 times

you can see now four vertices are moving together. You could say the "limits" that are moving are the union of black and orange edges. This means the "limits" now are an entire part of the polytope, rather than only edges.

now finally the negative nodes. These select vertices form outside the mirrors to move together with the vertices inside those mirrors. Look at the following picture:

x6x(.3.) intern.png (54.32 KiB) Viewed 142095 times

It's a bit of a mess, but I hope you can recognize the starting dodecagon: look at the vertices at the tails of the arrows, these form a dodecagon. You can see some of these vertices are attached to red/orange edges, these form a A3x, and some are attached to green edges, these form a (-x)3(A+x). When everything expands, the (A+x)-edge of (-x)3(A+x) moves together with the x-edge of the A3x. this means the x||(A+x)-thing moves, and thus the x||(A+x) is the "limit".
Now the same way, when we expand ike, fox2xfo2oxf&#zx => Fxo2xfo2oxf&#zx, the "limits" are an x-edge, a f2o-rectangle and a f-edge that's perpendicular in orientation to the x-edge. These things can be spotted in the animations of ike-bilbiro, as the parts that move together. When we expand ike=>thawro, the limits are the colored parts in quickfurs animation of ike=>thawro: . So our "partial Stott-expansions" basically move parts of the polytope radially outwards. Now the two things I can think of that should be true are:
1. the part that is moving outwards must be CRF
2. the new things that are made where things are pulled apart have to be CRF.

[Klitzing]

I like your explanatory sketches. But that anymated gif (ike <-> thawro) - as well as that other one, not shown here (ike <-> bilbiro) - suffers from the obscuring fact that they include additionally the hull operation, which definitely is not part of that Stott stuff. You rather should extract the mere Stott stuff by deviating into the realm of non-convexity.

Corresponding pics have been constructed already, cf.

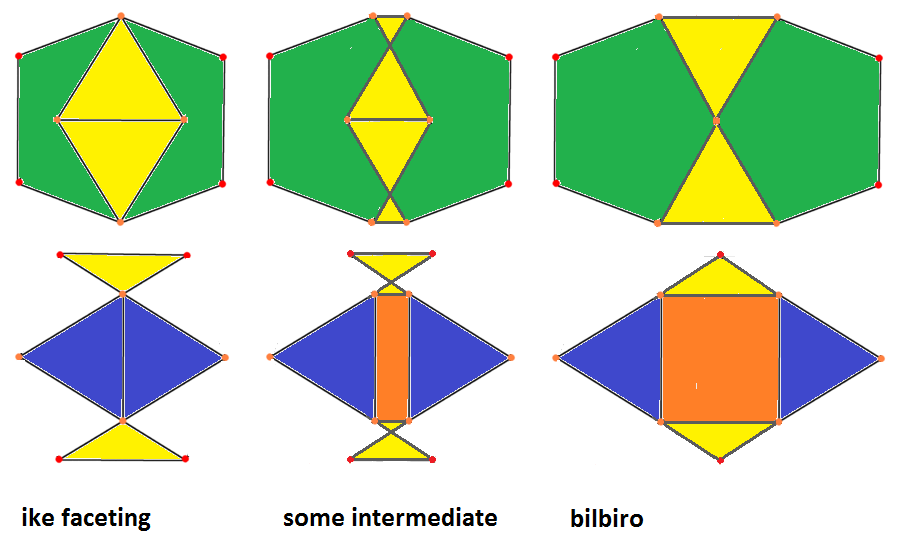
resp.

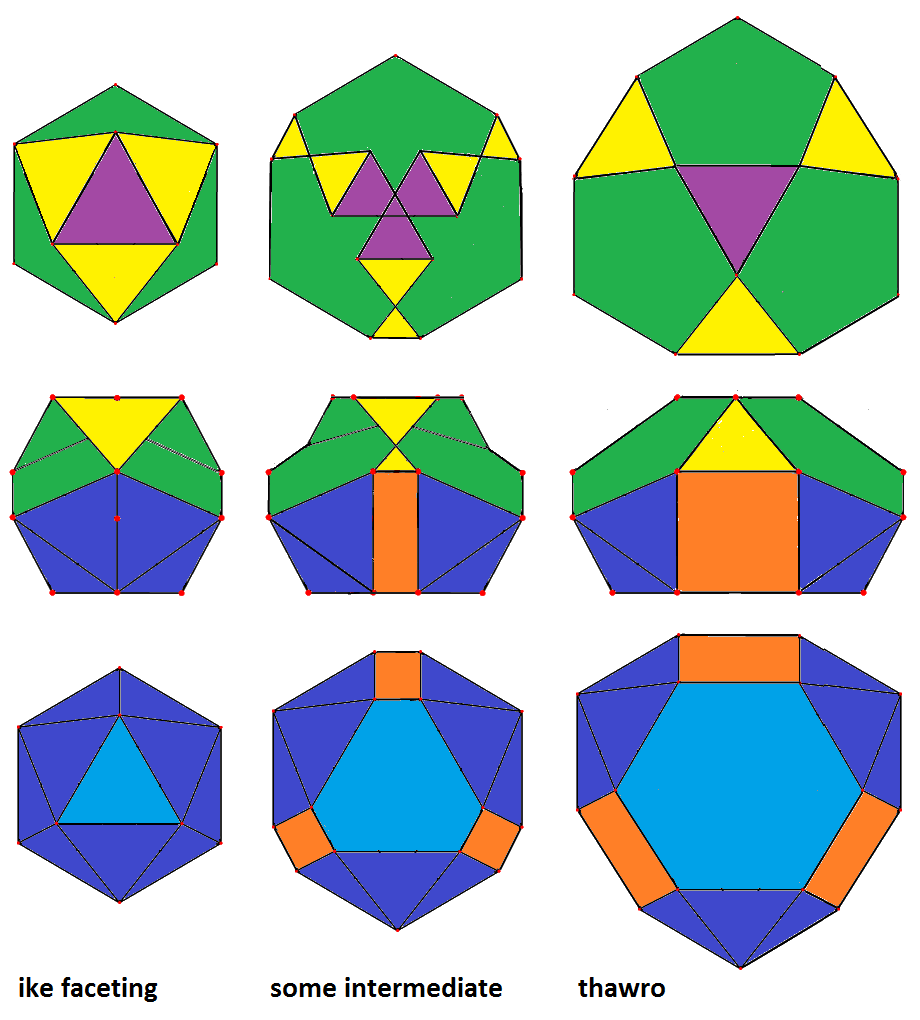
(If still being clipped in fullscreen mode then take refuge to my website, where these pics are displayed in a scaled version. - Don't know how to do that in here by means of that pseudo-html editor ...)

--- rk

[wendy]

In relation to student91's diagram, the expansion of the red hexagon into a red+black dodecagon, goes from (r)6(o) to (r)6(k), where (r) and (k) are lengths. Although the blue vector is the real vertex-vector of (k), we measure length along the black line, because we use edge lengths usually. The blue vector and the black edge are both half-an-edge from the line that bisects the mirror between the blue edges.

Thanks for finding the paper! I've downloaded it, it seems pretty much what i imagined to be in it.

[Klitzing]

Thanks for finding the paper! I've downloaded it, it seems pretty much what i imagined to be in it.

I already had got some scans (both in tif and gif form) of the paper. Sadly the pages 2-6 of the pdf were missing so far.

It now occured to me, that the publication date (edition of the "DEEL XI" on page 1 of the pdf) was 1913 (as I refered to so far on my webpage), while on page 6 of the pdf it seems to be the submission date provided additionally, where it states 1910 in contrast! - Surprising detail, ain't it?


While re-reading it now once more, I even found that Alicia herself used the term "partial operations" (page 15 of the pdf) when refering to the application of expansion to the triangular "limits" (faces) only in the transition from cuboctahedron towards truncated cube. Thus my term of "partial Stott expansion / contraction / operation" already got a precursor. But still, my idea would have been new. As she there is still using full symmetry again, "partial" there was just refering to a subset of "limits" (facets).

In this context it should be noted that the transitions of the yesterday provided pics of "true" transitions from faceted ike to bilbiro resp. from (differently) faceted ike to thawro (as well as the there not yet provided further one from even differnt faceted ike to pocuro) all are partial in Alicia's sense only: they use a subset of faces, which have to be expanded, not a subsymmetry! It only surpasses Alicia's setup, that expansions would not be normal to the corresponding "limits" but here rather orthogonal to the axial symmetry of the objects.

In contrast in my partial expansions, eg. from oct to esquidpy (J15) even uses still all faces, but breaks the former symmetry instead! (Whereas in the following steps of that very sequence, i.e. from esquidpy to squobcu (J28), resp. from squobcu to sirco it then would be "partial" in the sense of student91 again only (subset of faces moving non-necessarily in face-normal directions, but using the full symmetry of the starting figures).

So we get thus 3 different levels of "partial Stott expansions" now! Only levels 2 and 3 really are extrapolations of Alicia's original applications (i.e. provided examples´- we surely cannot know what else she already had in mind in those days, but not having written down then).

--- rk

[Klitzing]

Code: Select all

bilbiro
oxFxo 2 ofxfo &#xt

-> : (-x) 2 (-o)
<- : (+x) 2 (+o)

ike faceting
(-x)ofo(-x) 2 ofxfo &#xt


Code: Select all

thawro
oxFx 3 xfox &#xt

-> : (-x) 3 (-o)
<- : (+x) 3 (+o)

ike faceting
(-x)ofo 3 xfox &#xt


Code: Select all

pocuro
xoxx 5 ofxo &#xt

-> : (-x) 5 (-o)
<- : (+x) 5 (+o)

ike faceting
o(-x)oo 5 ofxo &#xt


--- rk

[student91]

[...]
While re-reading it now once more, I even found that Alicia herself used the term "partial operations" (page 15 of the pdf) when refering to the application of expansion to the triangular "limits" (faces) only in the transition from cuboctahedron towards truncated cube. Thus my term of "partial Stott expansion / contraction / operation" already got a precursor. But still, my idea would have been new. As she there is still using full symmetry again, "partial" there was just refering to a subset of "limits" (facets).

As far as I got it, in that part she was describing contractions of octahedral polytopes according to tetrahedral subsymmetry, resp. contractions of tesseractic polytopes according to demitesseractic symmetry. She describes:
½e₂O=tT, that is o4o3x (O) = o3x3o => x3x3o (½e₂O), or o4o3x => s4o3x with snub-nodes
½c₀c₀e₁C=T, that is x4o3o (C) => x4x3o (e₁C)=> o4x3o (c₀e₁C)= x3o3x => o3o3x (½c₀c₀e₁C)
½c₀c₀e₁C₈=C₁₆, that is, x4o3o3o (C₈)=> x4x3o3o (e₁C₈)=> o4x3o3o (c₀e₁C₈) = x3o3x*b3o => x3o3o*b3o (½c₀c₀e₁C₈).
Thus she describes full Stott-contractions, but according to a subsymmetry. This part thus treats the overlap between tetrahedral and octahedral symmetry, resp. that of tessic and demitessic symmetry. I guess nowadays, we won't really call this partial expansion resp. contraction.

In this context it should be noted that the transitions of the yesterday provided pics of "true" transitions from faceted ike to bilbiro resp. from (differently) faceted ike to thawro (as well as the there not yet provided further one from even different faceted ike to pocuro) all are partial in Alicia's sense only: they use a subset of faces, which have to be expanded, not a subsymmetry! It only surpasses Alicia's setup, that expansions would not be normal to the corresponding "limits" but here rather orthogonal to the axial symmetry of the objects.

In contrast in my partial expansions, eg. from oct to esquidpy (J15) even uses still all faces, but breaks the former symmetry instead! (Whereas in the following steps of that very sequence, i.e. from esquidpy to squobcu (J28), resp. from squobcu to sirco it then would be "partial" in the sense of student91 again only (subset of faces moving non-necessarily in face-normal directions, but using the full symmetry of the starting figures).
[...]
--- rk

I'm not sure what you ment here, my expansions clearly are with respect to a full subsymmetry. It is because of this subsymmetry, that we get more than one set of vertices, together making a full set of faces and stuff. A expansion of ike with a subset of faces could be x3o5o=>(-x)3x5o=>o3x5o. you take the x5o-faces that are hidden in ike (the faces of the great dodecahedron) and move them outwards. My partial expansions use a subsymmetry, so ike x3o5o has a axial subsymmetry, fox2xfo2oxf&#zx. when you expand this, you first change it in fox2xfo2of(-x)&#zx, then you add x to the right group of nodes. This makes two sets of fox2xfo(2xoF)&#zx move outwards (two pentagons together with two triangles). This clearly is according to axial subsymmetry. I don't think it differs that much from oct=>esquidpy, as that is qoo2oqo2ooq&#zx, expanded. The "limits" that are moving are qoo2oqo(2ooq)&#zx, which is a square pyramid. Thus oct=>esquidpy is, just as ike=>bilbiro, an expansion according to axial subsymmetry, if I'm right. not that the whole partial expansion chain of oct=>sirco can be described in axial subsymmetry: qoo2oqo2ooq&#zx => qoo2oqo2xxw&#zx => qoo2xwx2xxw&#zx => wxx2xwx2xxw&#zx. So this is a chain of partial expansions according to my definition. this is different from ike=>bilbiro in that that one doesn't give a chain of expansions. It might very well be that my definition is the same as yours.

[Klitzing]

[...]In this context it should be noted that the transitions of the yesterday provided pics of "true" transitions from faceted ike to bilbiro resp. from (differently) faceted ike to thawro (as well as the there not yet provided further one from even different faceted ike to pocuro) all are partial in Alicia's sense only: they use a subset of faces, which have to be expanded, not a subsymmetry! It only surpasses Alicia's setup, that expansions would not be normal to the corresponding "limits" but here rather orthogonal to the axial symmetry of the objects.

In contrast in my partial expansions, eg. from oct to esquidpy (J15) even uses still all faces, but breaks the former symmetry instead! (Whereas in the following steps of that very sequence, i.e. from esquidpy to squobcu (J28), resp. from squobcu to sirco it then would be "partial" in the sense of student91 again only (subset of faces moving non-necessarily in face-normal directions, but using the full symmetry of the starting figures).
[...]
--- rk

I'm not sure what you ment here, my expansions clearly are with respect to a full subsymmetry. It is because of this subsymmetry, that we get more than one set of vertices, together making a full set of faces and stuff. A expansion of ike with a subset of faces could be x3o5o=>(-x)3x5o=>o3x5o. you take the x5o-faces that are hidden in ike (the faces of the great dodecahedron) and move them outwards. My partial expansions use a subsymmetry, so ike x3o5o has a axial subsymmetry, fox2xfo2oxf&#zx. when you expand this, you first change it in fox2xfo2of(-x)&#zx, then you add x to the right group of nodes. This makes two sets of fox2xfo(2xoF)&#zx move outwards (two pentagons together with two triangles). This clearly is according to axial subsymmetry. I don't think it differs that much from oct=>esquidpy, as that is qoo2oqo2ooq&#zx, expanded. The "limits" that are moving are qoo2oqo(2ooq)&#zx, which is a square pyramid. Thus oct=>esquidpy is, just as ike=>bilbiro, an expansion according to axial subsymmetry, if I'm right. not that the whole partial expansion chain of oct=>sirco can be described in axial subsymmetry: qoo2oqo2ooq&#zx => qoo2oqo2xxw&#zx => qoo2xwx2xxw&#zx => wxx2xwx2xxw&#zx. So this is a chain of partial expansions according to my definition. this is different from ike=>bilbiro in that that one doesn't give a chain of expansions. It might very well be that my definition is the same as yours.

My point was that both, the faceting of ike, which I showed up, and your vertex representation of ike within that subsymetry (it should read rather fox2xfo2o(-x)f&#zx, I suppose) already break the global symmetry before we even apply Stott expansion.

As you correctly point out, the transitions are

• fox2xfo2o(-x)f&#zx + (+o)2(+o)2(+x) = fox2xfo2xoF&zx
• qoo2oqo2ooq&#zx + (+o)2(+o)2(+x) = qoo2oqo2xxw&#x

But you can see that you (first line) need to start with an assymmetric version, while I (second line) start with the full symmetrical one. That is the tiny, but crucial difference.

(My subsequent chain does not contribute to the argument. In fact, at the start of the second transition, the former symmetry already has been broken.)

--- rk

[Klitzing]

[...]
While re-reading it now once more, I even found that Alicia herself used the term "partial operations" (page 15 of the pdf) when refering to the application of expansion to the triangular "limits" (faces) only in the transition from cuboctahedron towards truncated cube. Thus my term of "partial Stott expansion / contraction / operation" already got a precursor. But still, my idea would have been new. As she there is still using full symmetry again, "partial" there was just refering to a subset of "limits" (facets).

As far as I got it, in that part she was describing contractions of octahedral polytopes according to tetrahedral subsymmetry, resp. contractions of tesseractic polytopes according to demitesseractic symmetry. She describes:
½e₂O=tT, that is o4o3x (O) = o3x3o => x3x3o (½e₂O), or o4o3x => s4o3x with snub-nodes
½c₀c₀e₁C=T, that is x4o3o (C) => x4x3o (e₁C)=> o4x3o (c₀e₁C)= x3o3x => o3o3x (½c₀c₀e₁C)
½c₀c₀e₁C₈=C₁₆, that is, x4o3o3o (C₈)=> x4x3o3o (e₁C₈)=> o4x3o3o (c₀e₁C₈) = x3o3x*b3o => x3o3o*b3o (½c₀c₀e₁C₈).
Thus she describes full Stott-contractions, but according to a subsymmetry. This part thus treats the overlap between tetrahedral and octahedral symmetry, resp. that of tessic and demitessic symmetry.

Hmmm, you might get a point here. She indeed considered (rare) occasions of subsymmetric operations too. But her notation as ½c₀ or ½e₂ show on the other hand, that she was not aware of the general concept of subsymmetrical applications. She just knew of the relation between hypercubical and demihypercubical polytopes, which happen to scale in elemtal counts in this ratio. For being aware of the general setup she would have used something different than this bluddy "½", I'd suppose.

... I guess nowadays, we won't really call this partial expansion resp. contraction.

In fact, this exactly is, what partial (=subsymmetrical) expansion is about!

--- rk

[student91]

My point was that both, the faceting of ike, which I showed up, and your vertex representation of ike within that subsymetry (it should read rather fox2xfo2o(-x)f&#zx, I suppose) already break the global symmetry before we even apply Stott expansion.

As you correctly point out, the transitions are

• fox2xfo2o(-x)f&#zx + (+o)2(+o)2(+x) = fox2xfo2xoF&zx
• qoo2oqo2ooq&#zx + (+o)2(+o)2(+x) = qoo2oqo2xxw&#x

But you can see that you (first line) need to start with an assymmetric version, while I (second line) start with the full symmetrical one. That is the tiny, but crucial difference.

(My subsequent chain does not contribute to the argument. In fact, at the start of the second transition, the former symmetry already has been broken.)

--- rk

[...]

... I guess nowadays, we won't really call this partial expansion resp. contraction.

In fact, this exactly is, what partial (=subsymmetrical) expansion is about!

--- rk

ah, okay, that clears things up. Btw, has wendy's "values on nodes" devise been published, or is it something that's only used on this forum? i.e. do you have any reference to an article that introduces this device, or do we have to explain that in the article we're going to write (or an article we'll write just before we write the one about partial expansions)

[wendy]

Wendy has not written it up because she has no clue how to publish things. :S

[student91]

Recently I've found another partial expansion of ex (one that gives bilbiro's): take the .5.3.-representation of ex:
o3o5o||x3o5o||o3o5x||f3o5o||o3x5o||f3o5o||o3o5x||x3o5o||o3o5o
As I've explained before, on the equator are hidden ikes in .2.2.-orientation. We've already expanded these ikes two ways (one gave castellated x5o3x-prism, one gave bilbiro'd o5o3x3o). These two ways are both done by adding an x to all parts of the polytope(see my first post on this topic). The third one should be done differently. This time we move the layers themselves apart. This gives us:
o3o5o||x3o5o||o3o5x||o3x5o||f3o5o||o3x5o||o3o5x||x3o5o||o3o5o
The bilbiro's can be revealed by deleting corresponding vertices of the id's.
Maybe we want to add x to some representation of ex that would give us this. The representation we would need is 3-dimensional. Such 3d-representations follow pretty straightforward from what we know from lace-cities and lace-towers. In 3D, we have lace-cities with single nodes. This is a 2D-representation with 1D-subsymmetry, and 2+1=3D. We also have lace-towers: 1D-representations with 2D-subsymmetry (again, 1+2=3D). (we could also take 0D-representations with 3D-subsymmetry (the original dynkin-diagram), and 3D-representations with 0D-subsymmetry (all it's vertices placed in space), but these are limiting representations that don't add anything). in 4D we have 2D-representations with 2D-subsymmetry, and 1D-representations with 3D-subsymmetry. 3D-representations with 1D-subsymmetry would have nodes (x,f,F etc.) placed in a 3D space. The case we want has: 1 node at the center with value 2f, 12 nodes placed at the vertices of an ike with value F, 20 nodes placed at the vertices of a doe with value f, another 12 nodes on the vertices of a (bigger) ike with value x, and finally 30 vertices with value o. First we change all x's in (-x)'s, then we add an x to everything, and we get the thing I described. (if we don't change x's in (-x)'s, we get an elongated ex, oxofoofoxo3ooooxxoooo5ooxooooxoo&#xt)

In this representation, I would like to clarify what node I'm using. I think I will do this by denotating x3.3.5. or something.
You might notice the .3x5x3x-representation describes the places of the nodes of the x3.3.5.-representation. We could say they are "inverse representations". I haven't investigated these inversions very much yet, I'm still unable to "wrap my mind around it". anyway, the 2D-representations with 2D-subsymmetry seem to be self-inverse, and the 1D-representations with 3D-subsymmetry seem all to inverse to a 1D-representation.

But as I've changed to nodes to describe subsymmetries, we can easilly say ho many "true" subsymmetries we have to check (I mean those that are in the dynkin graph, and thus subdimensional.) it's 2^4-2=14. that's unconveniently much. One positive thing is that only ike seems to admit 3d partial expansions, so we only have to check things with ikes. There are 3 of these, so we have to check 14*3=42, which is much less than 174 segmentochora.

[Klitzing]

Recently I've found another partial expansion of ex (one that gives bilbiro's): take the .5.3.-representation of ex:
o3o5o||x3o5o||o3o5x||f3o5o||o3x5o||f3o5o||o3o5x||x3o5o||o3o5o
...
This time we move the layers themselves apart. This gives us:
o3o5o||x3o5o||o3o5x||o3x5o||f3o5o||o3x5o||o3o5x||x3o5o||o3o5o
...

so you just exchange the usages of equatorial and tropal layers? - As ex had a circumsphere the circumradius of o3x5o would be larger than that of f3o5o. So this might lead to non-convexity at the new equatoral layer. - ?

(At the dodecahedral layer the bend between the ike||doe and the doe||id segmentochora at least does not come out non-convex. This is because the latter segmentochoron is just an icosa-diminishing of the bistratic ex segment o3o5x||f3o5o||o3x5o. - Essentially skipping the center vertices of the new paps. - So here we would be okay.)

... Such 3d-representations follow pretty straightforward from what we know from lace-cities and lace-towers. In 3D, we have lace-cities with single nodes. This is a 2D-representation with 1D-subsymmetry, and 2+1=3D. We also have lace-towers: 1D-representations with 2D-subsymmetry (again, 1+2=3D). (we could also take 0D-representations with 3D-subsymmetry (the original dynkin-diagram), and 3D-representations with 0D-subsymmetry (all it's vertices placed in space), but these are limiting representations that don't add anything). in 4D we have 2D-representations with 2D-subsymmetry, and 1D-representations with 3D-subsymmetry. 3D-representations with 1D-subsymmetry would have nodes (x,f,F etc.) placed in a 3D space.

Hmm, sounds like extending from lace towers (1D positioning space, (n-1)D subsymmetry space) via lace cities (2D positioning space, (n-2)D subsymmetry space) now towards the next step, say lace universes (3D positioning space, (n-3)D subsymmetry space)!   - (Hope Wendy would support that term. )

(So far my preliminary comments. For the remainder of your post I have to look a bit deeper into that first. )

--- rk

[Klitzing]

Recently I've found another partial expansion of ex (one that gives bilbiro's): take the .5.3.-representation of ex:
o3o5o||x3o5o||o3o5x||f3o5o||o3x5o||f3o5o||o3o5x||x3o5o||o3o5o
As I've explained before, on the equator are hidden ikes in .2.2.-orientation. We've already expanded these ikes two ways (one gave castellated x5o3x-prism, one gave bilbiro'd o5o3x3o). These two ways are both done by adding an x to all parts of the polytope(see my first post on this topic). The third one should be done differently. This time we move the layers themselves apart. This gives us:
o3o5o||x3o5o||o3o5x||o3x5o||f3o5o||o3x5o||o3o5x||x3o5o||o3o5o
The bilbiro's can be revealed by deleting corresponding vertices of the id's.
Maybe we want to add x to some representation of ex that would give us this. The representation we would need is 3-dimensional. Such 3d-representations follow pretty straightforward from what we know from lace-cities and lace-towers. In 3D, we have lace-cities with single nodes. This is a 2D-representation with 1D-subsymmetry, and 2+1=3D. We also have lace-towers: 1D-representations with 2D-subsymmetry (again, 1+2=3D). (we could also take 0D-representations with 3D-subsymmetry (the original dynkin-diagram), and 3D-representations with 0D-subsymmetry (all it's vertices placed in space), but these are limiting representations that don't add anything). in 4D we have 2D-representations with 2D-subsymmetry, and 1D-representations with 3D-subsymmetry. 3D-representations with 1D-subsymmetry would have nodes (x,f,F etc.) placed in a 3D space. The case we want has: 1 node at the center with value 2f, 12 nodes placed at the vertices of an ike with value F, 20 nodes placed at the vertices of a doe with value f, another 12 nodes on the vertices of a (bigger) ike with value x, and finally 30 vertices with value o. First we change all x's in (-x)'s, then we add an x to everything, and we get the thing I described. (if we don't change x's in (-x)'s, we get an elongated ex, oxofoofoxo3ooooxxoooo5ooxooooxoo&#xt).

Hmmm, if i get it correctly, 3x1 = 1x3, that is, you reconsider ex as lace tower again. But instead of handling the x's in para-space (symbol space) you rather handle those of perp-space (stacking alignment) now. Changing there x's into (-x)'s then would tell to go to and thro' accordingly rather than consecutively along this axial direction. For mere segmentochora (monostratic segments) this surely would be allowed (even so this generally would deviate from convexity! *) But be aware, that this would clearly dissect those cells, which would stretch thru more than one such segment, into an according number of cell segments!

(* Sure, you won't stick with just this replacement, but apply some x-addition thereon. So it would require to consider the final outcome instead of some intermediate figure.)

I further noticed, that your procedure surely would handle all outer layers alike, as there no (-x)'s would occure. They are just shifted out a bit. The main effect here is restricted to the first tropal layer, i.e. the region of the 3 medial layers. So we also could chopp off both outer caps and consider that medial region solely. Then it happens that you just transform f3o5o||o3x5o||f3o5o into o3x5o||f3o5o||o3x5o. - It should be noted however, that the large triangles of f3o5o occure in ex as medial sections within the segmentochora o3o5x (|| f3o5o) || o3x5o. In fact the vertices of f3o5o would be the centers of the paps in that segmentochoron. But then one notes that these vertices clearly are connected to both the id and doe, but that there are also lots of edges running thru, from doe to id directly! And therefore faces too, which get dissected at this level. Thus your inverse stacking o3x5o||f3o5o||o3x5o thus looks like having lots of broken lacing faces. - Or are you able to rearrange all these cell-bits somehow?

--- rk

[student91]

I'm not sure if you did understand what I ment to happen with changing x's in (-x)'s, so I'll try to explain that again.
first of all, I could denotate the 3D-representation of ex as (2f)(o5o3o)+(F)(o5o3x)+(f)(x5o3o)+(x)(o5o3f)+(o)(o5x3o). The first thing means what node it is, and the second thing how that would be placed in 3D. (now that I've written it down, it is much neater than I thougt).
if we add x to all first nodes, we get this:
[o5o3o||o5o3x||x5o3o||o5o3f||o5x3o]<=>[o5x3o||o5o3f||x5o3o||o5o3x||o5o3o]
"limit 1" <=(moved away from)=> "limit 2"
if we change the (x)(o5o3f) to (-x)(o5o3f), this would change the limits:
[o5o3o || o5o3x || x5o3o || (o5o3f||) o5x3o || o5o3f] <=> [o5o3f || o5x3o (||o5o3f) || x5o3o || o5o3x || o5o3o]
"limit 1" <=(moved away from)=> "limit 2"
The things in parenthesis aren't part of the limits. (you can compare this with my drawing of dodecagon=>something ugly, it made some vertices come from beyond the mirror, this is the same)
So what I do when I change the x in (-x) is, that I make the f-ike part of the far side of ex, instead of the near side. This can be done, because the f-ike's vertices can be removed, so the interconnectivity of everything around these vertices makes it possible instead of impossible.

Now the (x)(o5o3f) makes an x2f-rectangle that is part of an equatorial ike pyramid, and this ike-pyramid becomes an bilbiro-pseudopyramid, so I guess it will be CRF, though I'm not completely sure.

[student91]

That last post of me gave me an idea for denotation lace-cities, lace towers and all of that kind in one general way. take, for example ike. Klitzing has a lace-city of that on his site. This lace-city would be described, in my new way, as (f)(x2o)+(x)(o2f)+(o)(f2x). This means: there are f-nodes placed at the vertices of an x2o-"rectangle", and there are x-nodes placed at the vertices of an o2f-"rectangle", and finally you have o-nodes placed on the vertices of an f2x-rectangle. When you draw this, you get the lace-city on Klitzings site.
Funny thing is, that the inversion of this, (x2o)(f)+(o2f)(x)+(f2x)(o) makes a representation of ike as well. (we then have two x2o-things placed on the vertices of a f-line, two o2f-things placed on the vertices of an x-line, and finaly twoone f2x-things on the vertices of an o-"line", i.e. x2o||o2f||f2x||o2f||x2o, with the lengths of the lacings of equal layers given.)
This means every representation of ike has an inverse. In general, I think I can say every such representation can be inversed, and for every representation on Klitzings site, we can make a representation that describes both the nodes and the position of these things in the projection-space. (I don't want to replace Klitzings representations by mine, his representations are much more useful for cutting and pasting. My representation on the other hand give better insight in the symmetrical buildup of the polytopes.)
Unfortunately, this new way of describing doesn't decrease the number of representations we have to determine: all lace-cities seem to be self-inverse. take for example the .5.-representation of ex. It can be written as (o5o)(x5x)+(f5o)(o5x)+(o5f)(x5o)+(x5o)(o5f)+(o5x)(f5o)+(x5x)(o5o). You see both "node-space" and "projection-space" are .5., so they don't give new representations for free, as happens in 3d (every lace-tower gives a lace-city with very few effort)

[student91]

This new way to describe lace-structures is truely awesome . Look at the way I described the latest expansion of ex. I described it by shifting the 1D-representation. (so ...f3o5o||o5x3o||f3o5o... => ...o5x3o||f3o5o||o5x3o...) let's see that in the light of our new representation: (2f)(o5o3o)+(F)(o5o3x)+(f)(x5o3o)+(x)(o5o3f)+(o)(o5x3o) => (2f+x)(o5o3o)+(f+2x)(o5o3x)+(F)(x5o3o)+(-x=>o)(o5o3f)+(x)(o5x3o). So when we represent it in 1D-representation, the symbols shift places, but the nodes keep the same, and in the inverse representation, the symbols keep their position, and the nodes change.
Furthermore in the 1D-representation, we were able to identify the limits. (the limit was o5o3o||o5o3x||x5o3o||o5x3o||o5o3f) This is useful as the limits are the thnigs that are ment at 1 in my conditions:
1. the part that is moving outwards must be CRF
2. the new things that are made where things are pulled apart have to be CRF.
Of course the o5o3f at the end is not CRF, but 1 means only the part that is not on the boundary so to speak.
Now let's try this with something else, e.g. the .3.-expansion of ex. here is the lace-city of ex, according to .3.-symmetry.

Code: Select all

                o3o               
                                   
        x3o   o3f f3o   o3x       
                                   
                                   
o3o o3f   f3x       x3f   f3o o3o
                                   
   f3o       o3F   F3o       o3f   
                                   
                                   
o3x   x3f F3o   f3f   o3F f3x   x3o
                                   
                                   
   f3o       o3F   F3o       o3f   
                                   
o3o o3f   f3x       x3f   f3o o3o
                                   
                                   
        x3o   o3f f3o   o3x       
                                   
                o3o

With the new writing method, this would be written as
(f3o)(f3x)+(F3o)(o3x)
(o3f)(x3f)+(o3F)(x3o)+(f3f)(o3o)
(f3x)(f3o)+(o3x)(F3o)+(o3o)(f3f)
(x3f)(o3f)+(x3o)(o3F)
expansion gives:
(F3o)(f3x)+(A3o)(o3x)
(x3f)(x3f)+(x3F)(x3o)+(F3f)(o3o)
(F3x)(f3o)+(x3x)(F3o)+(x3o)(f3f)
(o3F)(o3f)+(o3x)(o3F)

Now we can project this two ways. One is already known, the other one shifts the positions of the .3.-lace city of ex. As we know, there will be three limits moving away from each other here. The "limit" can be found by projecting everything using the new positions (A3o etc.), but without mirroring around the mirror that is subject of expansion. You then get this:

Code: Select all

                o3o               
                                   
        x3o   o3f       o3x       
                                   
                                   
o3o o3f   f3x        x3f   f3o
                                   
                   F3o
                                   
                                   
o3x   x3f F3o   f3f   o3F
                                   
                                   
   f3o       o3F

this limit has to be checked for convexity. Yet we know we don't have to check for convexity at the boundaries of the limit. this means we only have to look if the cavities that are left by changing (-x) to x are convex, as we know the other parts are convex because they came from a convex polytope. The cavities in this case are made by changing positions of f3o and o3F. Both of these give convex cavities, so our limit is convex. Now we can draw the full lace-city, as we know it's nicely ocnvex:

Code: Select all

                o3o               
                                   
        x3o   o3f       o3x       
                                   
                                   
o3o o3f   f3x        x3f   f3o   o3x
                                   
                   F3o                  o3o
                              x3f
                                   
o3x   x3f F3o   f3f   o3F   F3o       o3f
                                   
                                   
   f3o       o3F         f3f        f3x   x3o
                                   
                                   
o3x   x3f F3o   f3f   o3F   F3o       o3f
                                   
                              x3f
                   F3o                  o3o       
                                   
o3o o3f   f3x        x3f   f3o   o3x
                                   
                                   
        x3o   o3f       o3x       
                                   
                o3o

[Klitzing]

what are these lace cities meant to describe, student91   - okay, now you filled text inbetween...
(the latter one does not look convex, I fear ...)   - okay, now you filled in the 3rd segment into this city as well...
--- rk

[student91]

those lace-cities were part of an unfinished post of mine. because I had to type on both my phone and my computer, I had to save my unfinished post somewhere, and I thought I could just post it quick enough for no one to notice it, but I failed. Anyway, does everyone understand what I've typed so far, as I think we're almost there when you understand what I've typed. I will eagerly explain anything that isn't clear.

[Klitzing]

... Thus your inverse stacking o3x5o||f3o5o||o3x5o thus looks like having lots of broken lacing faces. - Or are you able to rearrange all these cell-bits somehow?

Ehh, not too difficult, after all: isn't this just iddip (oo3xx5oo&#x) augmented by 12 pippies (ox2ox5oo&#x)?

If I get this correctly, then we have

• angle at 4-gon between pip and trip of iddip = 142.622632 degrees
• angle at 4-gon between pip and squippy of pippy = 13.282526 degrees
• angle at 5-gon between pip and id of iddip = 90 degrees
• angle at 5-gon between pip and peppy of pippy = 18 degrees

thus all combined angles ought be convex - at least within this bistratic segment.


(As such this is just kind a 4D analogon to J57, the triaugmented hexagonal prism:

• its squares then would get mapped to the trips,
• its both-base-connecting triangles to the squippies,
• its single-base-connected triangles to the peppies,
• its hexagons to the ids.)

--- rk

[student91]

Ehh, not too difficult, after all: isn't this just iddip (oo3xx5oo&#x) augmented by 12 pippies (ox2ox5oo&#x)?

If I get this correctly, then we have

• angle at 4-gon between pip and trip of iddip = 142.622632 degrees
• angle at 4-gon between pip and squippy of pippy = 13.282526 degrees
• angle at 5-gon between pip and id of iddip = 90 degrees
• angle at 5-gon between pip and peppy of pippy = 18 degrees

thus all combined angles ought be convex - at least within this bistratic segment.

Indeed. However, because It's made by expanding the 600-cell, it's much more interesting than just a dodecaaugmented iddip (although that's a way you could have discovered it, but then you don't account for it's awesome hidden structure).
My version of it would also have the rest of the 600-cell glued on top of it (that way it is a partial expansion, and thus it fits in our paper). Look what happens when we glue the rest on top of it: o5o3o||o5o3x||x5o3o||o5x3o ++ o5x3o||o5o3f||o5x3o ++ etc.
The dichoral angle of x5o3o||o5x3o at o5x of id is 72. This means the peppy of o5x3o||o5o3f||... will merge with the gyroelongated peppy of o5o3x||x5o3o||o5o3x to make an ike. Thus this expansion also has ikes.
What's even more interesting, though hard to demonstrate, is that it hides bilbiro's in it's structure. These can be shown with my new notation:
(F)(x5o3o)+(x)(o5x3o)+(o)(o5o3f) "=" (F)(x5o3o)+(x)(f5(-x)3x)+(o)(o5o3f).
look at it this way now:
(F)(x...o)+(x)(f...x)+(o)(o...f)
That is a bilbiro (just think there to be 2's everywhere, then you have F2x2o+x2f2x+o2o2f = Fxo2xfo2oxf&#zx = bilbiro.)
The fact that we had to change id (o5x3o)=>(f5(-x)3x) means the bilbiro is internal, so when we delete vertices of the id's, we will be able to see the bilbiro's.


Now why this CRF is quite interesting, is because it is the last one in a small family. Look at ex in my new notation:

Code: Select all

(2f) (o5o3o)       (2f) (o5o3o)
(F)  (o5o3x)       (F)  (o5o3x)
(f)  (x5o3o)       (f)  (x5o3o)      (f)..(x..o)
(x)  (o5o3f)       (x)  (o5o3f)      (x)..(o..f)   <=ike
(o)  (o5x3o)  "="  (o)(f5(-x)3x)     (o)..(f..x)


When you change o5x3o in f5(-x)3x, you can see the equatorial ikes in .2.2.-orientation, as highlighted above. As we know, fox2xfo2oxf&#zx can be expanded in 3 ways to get bilbiro's. (Fxo2xfo2oxf&#zx, fox2oFx2oxf&#zx and fox2xfo2xoF&#zx, the only difference in 3D is their orientation.)
In 4D, all these expansions can be done inside of ex:

Code: Select all

expansion on (.)(x5.3.)-node

(2f) (o5o3o)       (2f) (x5o3o)
(F)  (o5o3x)       (F)  (x5o3x)
(f)  (x5o3o)       (f)  (o5f3o)
(x)  (o5o3f)       (x)  (x5o3f)
(o)(f5(-x)3x)       (o)(F5(-x)3x) "=" (o)(x5x3o)
i.e. castellated x5o3x-prism

Code: Select all

expansion on (.)(.5.3x)-node

(2f) (o5o3o)       (2f) (o5o3x)
(F)  (o5o3x)       (F)  (o5x3o)
(f)  (x5o3o)       (f)  (x5o3x)
(x)  (o5o3f)       (x)  (o5o3F)
(o)(f5(-x)3x)       (o)(f5o3o)
i.e. "bilbiro'd o5o3x3o"

Code: Select all

expansion on (x)(.5.3.)-node

(2f) (o5o3o)       (F+f) (o5o3o)
(F)  (o5o3x)       (F+x)  ox5o3x)
(f)  (x5o3o)       (F)  (x5of3o)
(x)  (o5o3f)       (o)  (o5o3f)
(o)(f5(-x)3x)       (x)(f5(-x)3x)
i.e. my "new" discovery

Similar families can be made with other symmetries, but unfortunately, uniforms other than the 600-cell only exceptionally produce CRF's this way.

[Klitzing]

Ehh, not too difficult, after all: isn't this just iddip (oo3xx5oo&#x) augmented by 12 pippies (ox2ox5oo&#x)?

If I get this correctly, then we have

• angle at 4-gon between pip and trip of iddip = 142.622632 degrees
• angle at 4-gon between pip and squippy of pippy = 13.282526 degrees
• angle at 5-gon between pip and id of iddip = 90 degrees
• angle at 5-gon between pip and peppy of pippy = 18 degrees

thus all combined angles ought be convex - at least within this bistratic segment.

Indeed. However, because It's made by expanding the 600-cell, it's much more interesting than just a dodecaaugmented iddip (although that's a way you could have discovered it, but then you don't account for it's awesome hidden structure).

Well, it is true that it will occur just as a part (segment) within a larger structure, which deserves lots of interest on its own, but I think kind of minimalistic here: it is a smaller CRF, valid on itself. So, at least, worthwhile to mention!

My version of it would also have the rest of the 600-cell glued on top of it (that way it is a partial expansion, and thus it fits in our paper). Look what happens when we glue the rest on top of it: o5o3o||o5o3x||x5o3o||o5x3o ++ o5x3o||o5o3f||o5x3o ++ etc.
The dichoral angle of x5o3o||o5x3o at o5x of id is 72. This means the peppy of o5x3o||o5o3f||... will merge with the gyroelongated peppy of o5o3x||x5o3o||o5o3x to make an ike. Thus this expansion also has ikes.

I supposed that, but did not check last night, that these peppies would become corealmic with outer stuff. That is a nice coincidence!

What's even more interesting, though hard to demonstrate, is that it hides bilbiro's in it's structure. These can be shown with my new notation:
(F)(x5o3o)+(x)(o5x3o)+(o)(o5o3f) "=" (F)(x5o3o)+(x)(f5(-x)3x)+(o)(o5o3f).

Hmmm, we should be quite careful when using such "equalities"! Those are truely quite different things! o3x5o has faces being o3x . (unit triangles) and . x5o (unit pentagons). Whereas x3(-x)5f has faces x3(-x) . (doubly wound unit hexagons, kind of a double layer of 2 triangles), x . f (golden rectangles), and . (-x)5f ("complete" pentagons, i.e. unit pentagons with inscribed f-pentagrams). That is, the structure here is very different. - Instead, what you are after here, is just the set of vertices. That one indeed is the same. (So not very obvious without first evaluating the structure of that rather uncommon polyhedron.)

look at it this way now:
(F)(x...o)+(x)(f...x)+(o)(o...f)
That is a bilbiro (just think there to be 2's everywhere, then you have F2x2o+x2f2x+o2o2f = Fxo2xfo2oxf&#zx = bilbiro.)
The fact that we had to change id (o5x3o)=>(f5(-x)3x) means the bilbiro is internal, so when we delete vertices of the id's, we will be able to see the bilbiro's.

Same holds here: The bilbiroes probably are not truely contained as such, but the mere vertex set can be used to implement them, I suppose. - What I am after here all the time, is that the mere mechanics of your Dynkin symbol transformations is rather clear to me. But its implications onto esp. the face structures of the to be shifted elements is not described thereby and will have to be digged out separately. Consider e.g. the here used partial expansion of ike to bilbiro: that is, it is NOT ike, which gets expanded, it rather is some faceting thereof! - Same holds true in above's "equating". Again an example of some hidden (i.e. not mentioned) faceting.

Now why this CRF is quite interesting, is because it is the last one in a small family.

Indeed a truely worthwhile fact!

Look at ex in my new notation:

Code: Select all

(2f) (o5o3o)       (2f) (o5o3o)
(F)  (o5o3x)       (F)  (o5o3x)
(f)  (x5o3o)       (f)  (x5o3o)      (f)..(x..o)
(x)  (o5o3f)       (x)  (o5o3f)      (x)..(o..f)   <=ike
(o)  (o5x3o)  "="  (o)(f5(-x)3x)     (o)..(f..x)


When you change o5x3o in f5(-x)3x, you can see the equatorial ikes in .2.2.-orientation, as highlighted above. As we know, fox2xfo2oxf&#zx can be expanded in 3 ways to get bilbiro's. (Fxo2xfo2oxf&#zx, fox2oFx2oxf&#zx and fox2xfo2xoF&#zx, the only difference in 3D is their orientation.)
In 4D, all these expansions can be done inside of ex:

Code: Select all

expansion on (.)(x5.3.)-node

(2f) (o5o3o)       (2f) (x5o3o)
(F)  (o5o3x)       (F)  (x5o3x)
(f)  (x5o3o)       (f)  (o5f3o)
(x)  (o5o3f)       (x)  (x5o3f)
(o)(f5(-x)3x)       (o)(F5(-x)3x) "=" (o)(x5x3o)
i.e. castellated x5o3x-prism

Ehhmmm, "(f) (x5o3o) (f) (o5f3o)" looks like a typo, it must be hidden some deeper insight here! At least, direct application of mere expansion would result in (f) ((2x)5o3o) instead. - Ahh, you again did take implicite advantage of your "equations" first: x5o3o "=" (-x)5f3o, i.e. replacing the true dodecahedron by one which additionally uses the f-triangles underneath the vertices, and thus has to exchange the plain pentagons by "complete" ones.

Code: Select all

expansion on (.)(.5.3x)-node

(2f) (o5o3o)       (2f) (o5o3x)
(F)  (o5o3x)       (F)  (o5x3o)
(f)  (x5o3o)       (f)  (x5o3x)
(x)  (o5o3f)       (x)  (o5o3F)
(o)(f5(-x)3x)       (o)(f5o3o)
i.e. "bilbiro'd o5o3x3o"

Same here: "(F) (o5o3x) (F) (o5x3o)". I'd suspected (F) (o5o3(2x)) instead... - Well, suppose the same holds here as well, "equating" o5o3x and o5x3(-x) first. I.e. replacing the true icosahedron by a great dodecahedron together with doubled up (elsewhile canceling out) pseudo triangles.

Code: Select all

expansion on (x)(.5.3.)-node

(2f) (o5o3o)       (F+f) (o5o3o)
(F)  (o5o3x)       (F+x)  ox5o3x)
(f)  (x5o3o)       (F)  (x5of3o)
(x)  (o5o3f)       (o)  (o5o3f)
(o)(f5(-x)3x)       (x)(f5(-x)3x)
i.e. my "new" discovery

(where you already rewrote (on the left) that true icosidodecahedron o5x3o by f5(-x)3o ...)

Similar families can be made with other symmetries, but unfortunately, uniforms other than the 600-cell only exceptionally produce CRF's this way.

--- rk