The J92 rhombochoron and its derivatives

[quickfur]

I've been preparing the renderings of the J92 rhombochoron for April's Polytope of the Month on my website, and it occurred to me that it should be possible to augment its J92's with J92 pseudopyramids in a CRF way (the J92 pseudopyramid has very low height: only 1/phi for edge length 2, so the result should be convex). This would complete the J62's and produce a CRF with 6 icosahedra in triangular antiprismic symmetry.

This augmentation also causes some octahedra to appear in positions matching some of the square pyramids, indicating a possible derivation of the J92 rhombochoron as a diminishing of two relatively flat patches of the o5o3x3o's surface glued together like some analogue of a bicupola (the square pyramids would be bisected octahedra, if this derivation is correct). Of course, this still doesn't fully explain some of the other parts of the J92 rhombochoron, such as the triangular prism surrounded by 3 square pyramids and 2 tetrahedra, that seems to be analogous to Johnson's "luna" (triangle+square+triangle).

[Marek14]

I've been preparing the renderings of the J92 rhombochoron for April's Polytope of the Month on my website, and it occurred to me that it should be possible to augment its J92's with J92 pseudopyramids in a CRF way (the J92 pseudopyramid has very low height: only 1/phi for edge length 2, so the result should be convex). This would complete the J62's and produce a CRF with 6 icosahedra in triangular antiprismic symmetry.

This augmentation also causes some octahedra to appear in positions matching some of the square pyramids, indicating a possible derivation of the J92 rhombochoron as a diminishing of two relatively flat patches of the o5o3x3o's surface glued together like some analogue of a bicupola (the square pyramids would be bisected octahedra, if this derivation is correct). Of course, this still doesn't fully explain some of the other parts of the J92 rhombochoron, such as the triangular prism surrounded by 3 square pyramids and 2 tetrahedra, that seems to be analogous to Johnson's "luna" (triangle+square+triangle).

Let's see how the dichoral angles turn up:

Hexagon - rhombochoron: 60, pseudopyramid: 22.2388 - (bi)augmentation possible
Pentagon - rhombochoron: 144, pseudopyramid: 36 - augmentation possible, metabidiminished icosahedron fuses with pentagonal pyramid
Square - rhombochoron 135, pseudopyramid 20.9052 - augmentation possible
Triangle adjacent to hexagon - rhombochoron: 82.2388, pseudopyramid 22.2388 - augmentation possible
Second-layer triangle - rhombochoron 120, pseudopyramid 22.2388 - augmentation possible
Third-layer triangle - rhombochoron 30, pseudopyramid 22.2388 - augmentation possible
Top triangle - rhombochoron 120, pseudopyramid 22.2388 - (bi)augmentation possible

So, in total, there should be 1 augmented rhombochoron, 3 biaugmented rhombochora, 1 triaugmented rhombochoron and 1 tetraaugmented rhombochoron.

[quickfur]

Alright. Just as Marek has checked, the tetraaugmented J92 rhombochoron exists, and is CRF. My polytope viewer confirms that all edges are unit length. Here's a projection of it:



Here, we see 3 icosahedra surrounding the triangle closest to the 4D viewpoint. This indeed looks like a fragment of the o5o3x3o's surface, if you consider the outline of a pentagonal prism between the front and left icosahedra: it's actually a pentuplet of 2 octahedra and 3 square pyramids, the latter of which may be considered as bisected octahedra from the o5o3x3o's surface.

And now we see a continuation of the J92 rhombochoron's triangular prism + 2 tetrahedra + 3 square pyramid combo: now there are 3 such combos side-by-side linking the top triangular cupola to the bottom triangular cupola. Some of these square pyramids obviously belong to the o5o3x3o fragment; the rest I'm not so sure about. Together with the triangular prisms, they seem to be "bandages" that "patch up" the o5o3x3o fragment so that it interfaces with the far side of the polytope, where this arrangement of cell repeats, but in dual triangular orientation.

The pentagonal pyramids remain as mysterious as ever, since in o5o3x3o no icosahedra share faces with another icosahedron, so AFAICT these pentagonal pyramids are just struts that connect the two halves of the J92 rhombochoron together. OTOH, if we postulate that they are caps cut off from some other icosahedra, then, taken together with the tetrahedra, we see small fragments of the snub 24-cell here(!!). This would suggest the J92 rhombochoron is the diminished version of some sort of frankensteinian hybrid of o5o3x3o and the snub 24-cell, with triangular prisms as bandages to glue the pieces together!

So, I still can't figure out a derivation of the J92 rhombochoron from the uniform polychora. It seems to have quite a unique structure!

Question: what D number should we assign the augmentations of the J92 rhombochoron? I'd like to use D4.4.1 - D4.4.6 (according to Marek's count of augmentations), would that make sense?

[Marek14]

I have a suspicion that this tetraaugmented thing is some sort of 4D analogue to bilbro... patched together from surfaces of different polychora.

[student91]

Alright. Just as Marek has checked, the tetraaugmented J92 rhombochoron exists, and is CRF. My polytope viewer confirms that all edges are unit length. Here's a projection of it:



Here, we see 3 icosahedra surrounding the triangle closest to the 4D viewpoint. This indeed looks like a fragment of the o5o3x3o's surface, if you consider the outline of a pentagonal prism between the front and left icosahedra: it's actually a pentuplet of 2 octahedra and 3 square pyramids, the latter of which may be considered as bisected octahedra from the o5o3x3o's surface.

this image is interesting!! The fact that it has augmentations (or, needs a diminishing in order to show the thawros) makes me think that it is comparable with the thawrod/bilbirod o5o3x3o. These had patches of o5o3x3o and x5o3o3x. If the triangular prism-tetrahedron dichoral angle is equal to the corresponding angle of x5o3o3x, we know where that came from.
But what's more interesting, when you look at the ike's vertex most left and up, this is connected to the ike next to it via an edge. This edge seems to be the apex of a bilbiro pseudopyramid!! This would mean the rhombochoron has both room for bilbiro's and thawro's

[...]
So, I still can't figure out a derivation of the J92 rhombochoron from the uniform polychora. It seems to have quite a unique structure!

that's all I can tell about it's structure as well

Question: what D number should we assign the augmentations of the J92 rhombochoron? I'd like to use D4.4.1 - D4.4.6 (according to Marek's count of augmentations), would that make sense?

It does make sense, but do we really need a D-number for every augmentation? The bilbiro'd/thawro'd o5o3x3o also doesn't have listed all of it's possible diminishings. (Which is, in fact, just the inverse of what we're doing here) therefore, I suggest we only number the tetraaugmented one, call it D4.4.0 or D4.4.2

[student5]

Alright. Just as Marek has checked, the tetraaugmented J92 rhombochoron exists, and is CRF. My polytope viewer confirms that all edges are unit length. Here's a projection of it:



Here, we see 3 icosahedra surrounding the triangle closest to the 4D viewpoint. This indeed looks like a fragment of the o5o3x3o's surface, if you consider the outline of a pentagonal prism between the front and left icosahedra: it's actually a pentuplet of 2 octahedra and 3 square pyramids, the latter of which may be considered as bisected octahedra from the o5o3x3o's surface.

this image is interesting!! The fact that it has augmentations (or, needs a diminishing in order to show the thawros) makes me think that it is comparable with the thawrod/bilbirod o5o3x3o. These had patches of o5o3x3o and x5o3o3x. If the triangular prism-tetrahedron dichoral angle is equal to the corresponding angle of x5o3o3x, we know where that came from.
But what's more interesting, when you look at the ike's vertex most left and up, this is connected to the ike next to it via an edge. This edge seems to be the apex of a bilbiro pseudopyramid!! This would mean the rhombochoron has both room for bilbiro's and thawro's

[...]
So, I still can't figure out a derivation of the J92 rhombochoron from the uniform polychora. It seems to have quite a unique structure!

that's all I can tell about it's structure as well

this made me think the J92 rombochoron is similar to the D4.8.x series, they also have loads of options, together with a pretty similar orientation of bilbiro vs. thawro.
in fact, if you diminish the top, so that you get three bilbiroes centered around the top hexagon, and make a thawro from the bottom, you get tridiminished ikes, in the exact same orientation as D4.8.3

the bilbiroes are in the same orientation as D4.8.1, and even the surrounding cells are the same

the only difference lays in how these patches are put on top of each other.

now the question arises, if it is possible to augment the d.4.8.x series aswell, and how it would look i.e. would it also be a patch of the same cells? and would the J92 rombochoron it be deriveable from the D4.8 augmentation?
these two polychora seem to be made from the same operation, but at a different viewpoint or something, just like the partial stott-expansions give different shapes.
edit: after further tought, they both seem to have something to do with the hexagonal rotunda, where the projection envelope of J92 is a hexagonal orthobirontunda

[Keiji]

Btw., here is the incmats of that figure (in its full hexadecachoral symmetry):

@Keiji: add this to the D4.11 page?

Added.

I'm amazed by the similarity between this and D4.7! Though this polychoron is far simpler (25+1 positions instead of 67+1), the duals of both contain cubes, octahedra and rhombocupolawedges. D4.7 has been the first non-obvious dual (with an imat on the wiki, anyway) to contain either a cube or an octahedron, let alone both - and now they both show up in D4.11 too!

Question: what D number should we assign the augmentations of the J92 rhombochoron? I'd like to use D4.4.1 - D4.4.6 (according to Marek's count of augmentations), would that make sense?

Yes. D4.4 is already allocated, so it will stay as is, rather than becoming D4.4.0.

It does make sense, but do we really need a D-number for every augmentation? The bilbiro'd/thawro'd o5o3x3o also doesn't have listed all of it's possible diminishings. (Which is, in fact, just the inverse of what we're doing here) therefore, I suggest we only number the tetraaugmented one, call it D4.4.0 or D4.4.2

D-numbers are expendable. I think it's worth assigning D-numbers to every individual polytope, even inside (potentially large) families of similar polytopes, just in case wants to refer to something specific later. Plus, if we want to calculate explicit incidence matrices or coordinates etc. for these, a D-number is useful for referring to it, and giving its own wiki page.

[wendy]

Quickfur was asking about the lace-prism of the pentagonal uniforms in 4d. Here it is.

Here is the flat lace tower for the figures in {3,3,5}. The coordinate system is SSF, which means that 1 0 0 0 is read as x3o3o5o. The second figure gives the diameter-square, the usual measure for this parameter. The rest gives the vector difference, that 0 0 0 1 = 0 1 0 0 + a, where a = 0 1 0 -1.

The four vectors a,b,c,d all are equal to edge lengths, so the whole thing from o3x3o5o to x3o3x5x, forms a lace tower in its own right. You can check this by feeding the vectors o3x3o5xi, o3o3x5xi, x3x3xi5o, and x3xi3x5xi (where the i represents the negative value, that arises naturally on the short-chords of the supplement). So xi = -1, fi = -1.618 ... etc.

Code: Select all

  1 0 0 0    10.472136
  0 1 0 0    37.885438  *
  0 0 0 1    54.832815  a   0 1 0 -1
  0 0 1 0    82.249223  b   0 0 1 -1
  1 1 0 0    86.249223  c   1 1 -1 0
  1 0 0 1   109.665631  a
  1 0 1 0   147.554175  b
  0 1 0 1   181.442719  d   1 -1 1 -1
  0 1 1 0   229.803398  b
  0 0 1 1   270.164078  a
  1 1 0 1   274.164078  c
  1 1 1 0   332.996894  b
  1 0 1 1   379.829710  a
  0 1 1 1   506.439634
  1 1 1 1   653.993788


[student5]

the tetraaugmented J92 rombochoron turns out to be a (patch of) the triangularly stott expanded 600-cell. the one I tried to wrap my mind around earlier.

Code: Select all

                x3o               
                                  
        o3x   x3f F3o   x3x       
                                  
                                  
 x3o x3f   F3x       o3F   F3o x3o
                                  
   F3o       x3F   X3o       x3f   
                                  
                                  
x3x   o3F X3o   F3f   x3F F3x   o3x
                                  
                                  
   F3o       x3F   X3o       x3f   
                                  
 x3o x3f   F3x       o3F   F3o x3o
                                  
                                  
        o3x   x3f F3o   x3x       
                                  
                x3o               


it seems to be the patch on the top left, taking a section from x3x to x3x, you get

Code: Select all

                x3o               
                                  
        o3x   x3f F3o   x3x       
                                  
                                  
 x3o x3f   F3x
                                  
   F3o       x3F
                                  
                                  
x3x


which is half of J92 romb's lace city and everything you see in quickfur's render.

it just has to be mirrored around a point between F3x and x3F in order to complete the city

Code: Select all

                x3o               
                                  
        o3x   x3f F3o   x3x       
                                  
                                  
 x3o x3f   F3x       o3F
                                  
   F3o       x3F   f3x o3x
                                  
                                  
x3x   o3F f3x   o3x

        o3x


the lace city of tetraaugmented J92 rombochoron!
the thing I wonder about, is if the triangularly expanded ex is CRF, there are probably more patches to be cut from it, just as a lot of patches from the D4.8 series fit together (which is a patch of the tetrahedally stott-expanded ex)
thinking about that, I think a general rule applies for partial stott-expansions in 4D, and they are not that different from 3D
take a lace tower of any deltoid (such a thing with just triangles and stuff), for example this tower of ico, and choose a column to expand, change all x's according to the general rule, and start expanding

Code: Select all

o3x3o       o3x3o  x3(-x)3x    x3x3o  x3o3x
x3o3x -> (-x)3x3x  x3  o 3x -> o3x3x  x3x3x
o3x3o       o3x3o  x3(-x)3x    x3x3o  x3o3x


now these shapes aren't too complicated, so I'm pretty sure they are CRF,but maybe some more complicatad shapes do give problems, so I'll just try to expand ex ike-like

Code: Select all

o3o5o    o3o5o    x3o5o
x3o5o (-x)3x3o    o3x5o
o3o5x    o3o5x    x3o5x
f3o5o    f3o5o    F3o5o
o3x5o -> o3x5o -> x3x5o
f3o5o    f3o5o    F3o5o
o3o5x    o3o5x    x3o5x
x3o5o (-x)3x5o    o3x5o
o3o5o    o3o5o    x3o5o


guess this is CRF, I'm not completely sure however

[quickfur]

Alright. Just as Marek has checked, the tetraaugmented J92 rhombochoron exists, and is CRF.
[...]

[...]

[...]
But what's more interesting, when you look at the ike's vertex most left and up, this is connected to the ike next to it via an edge. This edge seems to be the apex of a bilbiro pseudopyramid!! This would mean the rhombochoron has both room for bilbiro's and thawro's
[...]

this made me think the J92 rombochoron is similar to the D4.8.x series, they also have loads of options, together with a pretty similar orientation of bilbiro vs. thawro.
in fact, if you diminish the top, so that you get three bilbiroes centered around the top hexagon, and make a thawro from the bottom, you get tridiminished ikes, in the exact same orientation as D4.8.3

Whoa. I think you're on to something!!! So here's the situation: the tetraaugmented J92 rhombochoron has 4 sets of 3 bilbiro-pyramid outlines that can be diminished, but you cannot simultaneously diminish both sets of bilbiro-pyramids around the same original J92 top triangle at the same time, because that would delete an edge from the bilbiro's. But you can diminish all 6 bilbiro-pyramids around a hexagonal face, to produce a new CRF with 6 bilbiroes that attach to each other via their pentagonal faces. Here's a render of this strange new beast:



Here, I'm projecting from a 4D viewpoint looking at the hexagon around which we diminished the bilbiro pyramids. The triplet of bilbiroes surrounding each octahedron outline only share edges with each other, but they share pentagonal faces with the bilbiros from the other triplet.

Note that I tweaked the 3D viewpoint so that this trigonal antiprismic symmetry is clearly seen; the 3D projection image is actually very narrow, so the central region in this projection that looks like a cuboctahedron is actually a pair of non-coplanar triangular cupolae.

Here's what the opposite side of the polychoron looks like:



Note that I left the J92 augmentations untouched, so the structure here is a bit more complicated than it would be otherwise. If we deleted the triangles that form the apices of the pseudo J92 pyramids, then we'd get two J92 cells on this side of the polychoron, which would produce a CRF with 6 bilbiro's and 2 thawro's.

[...]edit: after further tought, they both seem to have something to do with the hexagonal rotunda, where the projection envelope of J92 is a hexagonal orthobirontunda

Yeah I've noticed that. So there's definitely some kind of relationship between these CRFs. The D4.8.x series have overlapping patches of the hexagonal rotunda that form tetrahedral symmetry, whereas here we have a pair of hexagonal rotunda end-to-end. So they must derive from some common source somewhere, but just put together in different ways.

In any case, looks like there's an entire family of augmented/diminished CRFs here, directly related to the J92 rhombochoron, and also more distantly related to the D4.8.x series of CRFs. Clearly, we need to be looking at the various surface patches that give rise to these combinations, because enumerating each individual CRF would produce a very long list!

[student5]

[...]

[...]edit: after further tought, they both seem to have something to do with the hexagonal rotunda, where the projection envelope of J92 is a hexagonal orthobirontunda

Yeah I've noticed that. So there's definitely some kind of relationship between these CRFs. The D4.8.x series have overlapping patches of the hexagonal rotunda that form tetrahedral symmetry, whereas here we have a pair of hexagonal rotunda end-to-end. So they must derive from some common source somewhere, but just put together in different ways.

In any case, looks like there's an entire family of augmented/diminished CRFs here, directly related to the J92 rhombochoron, and also more distantly related to the D4.8.x series of CRFs. Clearly, we need to be looking at the various surface patches that give rise to these combinations, because enumerating each individual CRF would produce a very long list!

I tink this recurrence of patches is analogous to the ubiquity of Id's patches in stott-expanded 3D polyhedra, as I think both the J92 rombochoron and D4.8 are (modified) stott expansions. I think it'd be best to enumerate all different stott-expansions that are CRF (these are a lot aswell, since there are much more possiblle orientations in 4D)
just for fun: stott expanded ex's towers of which D4.8.4 and D4.8.2 are made: edit:they fit together at x3x3f, and form the (octa)augmented analog of the D4.8 series, the first one is center-expanded (the middle column) and in the other one, the left column is expanded

Code: Select all

x3x3o o3x3o    //edit
o3x3f x3o3f    x3x3o
o3F3o x3f3o    o3x3f //augmentation of A2, maybe this part can also be bilbiro'd?
f3x3x F3o3x    o3F3o
x3o3F x3x3f -> f3x3x //the point around which the second lace tower is rotated and stuck on the first
F3o3x F3x3o    x3o3F
x3x3f o3x3f    o3f3x //augmentation of B2, existent in B1
o3F3o x3f3o    f3o3x //augmentation of B1, existent in B2
f3x3o F3x3o    o3x3o
o3x3x x3o3x   


I do hope they are CRF, they must be for the part that is inside the D4.8 series
edit:a possible naming scheme for these expansions: middle-tetrahedally-stott-expanded 600 cell (m-tetstott ex) for the first and left-tetrahedally-stott-expanded ex (l-tetstott ex or r-tetstott ex, since they are the same)

[quickfur]

Here's a render of the far side with the J92 pyramids removed, leaving a pair of J92's:



The near side with the 6 bilbiros remains the same.

The derivation from the J92 rhombochoron is actually quite simple, and only affects one pair of J92's sharing a triangle:
- Identify a pair of J92's sharing a triangle
- Augment them with J92 pseudopyramids
- Delete their respective f3x vertices

[Marek14]

So, maybe we should consider the tetraaugmented version the basic polychoron with the others being various diminishings of it?

[quickfur]

So, maybe we should consider the tetraaugmented version the basic polychoron with the others being various diminishings of it?

That's a good idea.

[student5]

So, maybe we should consider the tetraaugmented version the basic polychoron with the others being various diminishings of it?

that'd be a good idea, and I guess renaming the D.4.8 series would be appropiate aswell, but I have no clue what to call them, except maybe call the augmented D.4.8 version l,m-tetrastott ex (but then the expansions need to be verified CRFs aswell)

another expansion, completely for free!
this'd be named l-penstott ex (pentagonal partial stott-expansion of ex in the left column)

Code: Select all

                 x5o           x5o                 
                        x5x                       
                                                   
            o5f                     o5f           
     x5o                                   x5o     
                        F5o                       
                 x5f           x5f                 
                                                   
     x5x                                   x5x     
            F5o                     F5o           
                                                   
x5o                     o5F                     x5o
                                                   
            x5f                     x5f           
     o5f                                   o5f     
                                                   
                 F5o           F5o                 
                        x5f                       
     x5o                                   x5o     
            x5x                     x5x           
                                                   
                        o5f                       
                 x5o           x5o                 


I somewhat have the idea these are CRF and if they are, the naming scheme could apply pretty effectively, thus the rombochoron could be called bi-l-tristott ex, as it has two patches of the l-tristott ex (triangular expansion of ex in the left row of the lace tower on Klitzing's site)'
edit: please tell me if I'm bloating the forum with these exapnsions and whether I should stop posting them until the first have been verified, or if I should start verification myself (I'm at loss as how to do this)

[student91]

So, maybe we should consider the tetraaugmented version the basic polychoron with the others being various diminishings of it?

That's a good idea.

That's why I suggested the tetraaugmented one to be called D4.4.0 We could call the normal one then D4.4 or D4.4.1 (or maybe D4.4(.1), with parentheses to prevent ambiguity.)
I don't like re-indexing the D4.8 CRF's though, that will cause big ambiguity with references in older posts. Note however, that the D4.8 series don't have a name yet. If you want, you can discuss naming it. (although I won't favor this to be discussed, when we don't know very much about their structure/relations)

[Marek14]

In my opinion we shouldn't be afraid to change the numbers because of older posts. Those posts are only a month or two old, it's not as if it's a decades-old convention

[Keiji]

edit: please tell me if I'm bloating the forum with these exapnsions and whether I should stop posting them until the first have been verified, or if I should start verification myself (I'm at loss as how to do this)

Not at all, space is not really an issue here; even if they are not verified, posting them here gives others a chance to verify them for you

[quickfur]

In my opinion we shouldn't be afraid to change the numbers because of older posts. Those posts are only a month or two old, it's not as if it's a decades-old convention

I don't like changing the numbers, because the D numbers are supposed to be arbitrary identifiers that uniquely identify a CRF, before we have enough information to name it properly. It's supposed to be a unique identifier that lets us refer to a specific CRF without fearing that a later (re)naming will mess up all the old references to it. In retrospect, I somewhat regret introducing the numerical suffixes that suggest some kind of grouping of these CRFs; it would have been better if we just used a single incrementing number instead.

The reason I say this, is because at this early stage, we simply don't have enough information to make a good decision about how to categorize (or name) these CRFs -- for example, we thought the J92 rhombochoron was a unique structure until we discovered "modified" partial Stott expansion, the J92 pseudopyramid, and now the connection of the J92 rhombochoron with the D4.8.x CRFs. In some sense, even the name "J92 rhombochoron" is, in retrospect, a bit premature, since now it's revealed to be just one instance of a wider class of CRFs with similar constructions.

So I'd rather leave the current D numbers as-is, perhaps even using a flat numbering system from now on (i.e., D4.13, D4.14, etc.) instead of D4.4.x -- because who knows, maybe later on we discover that our initial categorization was all wrong, and we have to rearrange the entire numbering hierarchy? In the interim, maybe we should introduce actual categories for these things, preferably on the wiki, with links to the D numbers of the members of each category.

(I'm tempted to say that we should use random numbers for the D number assignments from now on, to dispel the notion that the D numbers have any connection with chronology -- currently they do, but this limits them in other ways -- we now cannot retroactively assign a D number to some of the CRFs discovered before we started using D numbers, whereas many of those CRFs really do deserve such an identifier, especially those that are difficult to name because we're not sure where they fit in the scheme of things. Ideally, we should have wiki pages for each of them, so that we can upload .def files, .off files for them, link their projection images, etc., and have a unique ID that links to that page no matter how we may decide the rename these shapes later on.)

[quickfur]

Alright, two things:

• I renumbered the tetraaugmented J92 rhombochoron as D4.12, and the diminishing with 6 J91's and 2 J92's as D4.13.
• When updating the D number assignments, please do the assignments on Discovery index first, before adding it to another wiki page. This is so that there will be no inadvertent conflicting assignments.

I think from now on we should just assign D numbers linearly. Tentative category trees and such really should be done as new wiki pages (along the same lines as Bilbirothawroid).

[Keiji]

Numbering as something associated to a previously discovered polytope is a little easier to remember. We've already established the numbers mean nothing, only that there is some vague similarity between ones under the same "main" number. Can we not make D4.12 into D4.4.1 and D4.13 into D4.4.2?

[quickfur]

Numbering as something associated to a previously discovered polytope is a little easier to remember. We've already established the numbers mean nothing, only that there is some vague similarity between ones under the same "main" number. Can we not make D4.12 into D4.4.1 and D4.13 into D4.4.2?

Alright, alright, let's assign them to D4.4.1 and D4.4.2. I think it's a reasonable compromise.

EDIT: uploaded software models for them to D4.4.1 and D4.4.2.

[quickfur]

P.S. I skimmed over some older posts in this thread this morning, and realized that I'd forgotten to upload the software models for the D4.9.x polychora. Since I only actually constructed D4.9.1, I went and created a page for it, linked the render I made for it, and added the .def and .off files. Just in case people are interested to look at it. (Right, Marek? )

[Marek14]

P.S. I skimmed over some older posts in this thread this morning, and realized that I'd forgotten to upload the software models for the D4.9.x polychora. Since I only actually constructed D4.9.1, I went and created a page for it, linked the render I made for it, and added the .def and .off files. Just in case people are interested to look at it. (Right, Marek? )

Thanks

[Klitzing]

Hehe, PolyhedronDude always thinks about non-convex conjugates as well... - But I cannot wrap my mind around that one so far. It then should include the conjugates of bilbiro and teddi for cells. Several cells potentially might be used retrograde then too. - But instead of a try to build that one from scratch, just by "translation" of the final polychoron, one well could start from the conjugate of sadi, and then apply the same rebuild and expansion onto that. Perhaps this might be easier to follow...
[...]

Interesting. What's the general procedure for constructing a conjugate? Does it apply to any polytope? So far I only know of the conversion of icosahedron -> great icosahedron, but I'm not sure I understand the general procedure yet.

That's an easy one.

Consider the following:
replace within the Dynkin diagram any link -p/q- by -p/(p-q)-.

It happens to relate to a more general thing, not being restricted to Wythoffians only:

Consider the algebraic notation of vertex coordinates. And all the abstract incidence structure. Now maintain the latter, but switch every sqrt(2) by -sqrt(2) (for hypercubic type symmmetries) resp. every sqrt(5) by -sqrt(5) (for icosahedral and 600-cell type symmetries).

--- rk

[student5]

I tried to verify my (supposed) l-tetstott ex, but found out I got the lace tower of ex completely wrong
so, I tried to make a correct expansion of ex, but failed miserably again

Code: Select all

//original
x3o3o (-x)3x3o    o3x3o//this part is verified to be CRF, as in D.4.8
o3o3f    o3o3f    x3o3f
o3f3o    o3f3o    x3f3o
f3o3x    f3o3x    F3o3x
o3x3f    o3x3f    x3x3f
x3f3o (-x)3F3o    o3F3o //until here it follows D.4.8.x, this is also the point after which things get weird.
F3o3o    F3o3o    X3o3o //this can't stack properly with o3F3o
f3o3f -> f3o3f -> F3o3f // this won't stack with o3F3o or X3o3o either
o3o3F    o3o3F    x3o3F//this won't stack with o3F3o either
o3f3x    o3f3x    x3f3x //this will stack, with a height of 0,7071067812
x3o3f (-x)3x3f    o3x3f //stacks
o3f3o    o3f3o    x3f3o
f3o3o    f3o3o    F3o3o
o3o3x    o3o3x    x3o3x //stacks 0,2185080122 with F3o3o and 0,3535533906 with x3f3o


I think the problem lies in having no alternative to expanding F3o
and, when exploring that, I stumbled upon a way to alternatively expand anything, which is probably quite a powerful tool at hand, but gives us waaay many possibilities.

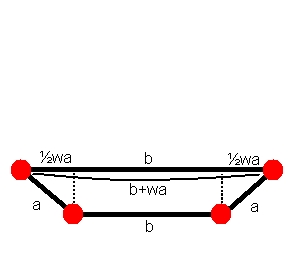
consider hexagon a3b, which "is the same as" (-a)3(b+a). If you expand this, you get hexagon (-a+1)3(b+a)

stuff.jpg

(124.31 KiB) Not downloaded yet

as is visible in the picture above, the edge length between the bottom two points is b+a-(-a+1), which is b+1.
in fact any hexagon a3b can thus be expanded as (a+1)3b or (a-1)3(b+1)

it goes even further than that, but I was too lazy to make a complete drawing for that, so here is the theory:
a random node is denoted as %
the length of the first shortcord belonging to a regular %-gon is w
according to student91's rule on negativity and stuff, x%o "=" (-x)%(wx) which can be mutliplied by anything, so a%o"="(-a)%(wa)
I don't know if it's already proven, but the drawing below shows that a%b "=" (-a)%(b+wa)

stuff2.jpg (16.56 KiB) Viewed 35486 times

if you stott-expand this, you get (-a+1)%(b+wa)
and if you substitute (-a+1) in a and (b+wa) in b and apply a%b "=" (-a)%(b+wa) again, you get
(-a+1)%(b+wa) "=" -(-a+1)%(b+wa)+w(-a+1)) = (a-1)%(b+w)
so any polygon a%b can be expanded either as (a+1)%b or (a-1)%(b+w)
edit:

[student5]

so the expansion I tried before, using this technique now is:

Code: Select all

x3o3o (-x)3x3o    o3x3o    o3x3o
o3o3f    o3o3f    x3o3f    x3o3f
o3f3o    o3f3o    x3f3o    x3f3o
f3o3x    f3o3x    F3o3x    F3o3x
o3x3f    o3x3f    x3x3f    x3x3f
x3f3o (-x)3F3o    o3F3o    o3F3o //until here it is verified
F3o3o (-F)3F3o (-f)3F3o    f3x3o //this stacks with o3F3o at a height of 0,1350453784 :-)
f3o3f =  f3o3f -> F3o3f =  F3o3f // this stacks with f3x3o at a height of 0,218...
o3o3F    o3o3F    x3o3F    x3o3f //from now on it should be CRF, beacause it is just a normal partial stott, without any inversions
o3f3x    o3f3x    x3f3x    x3f3x
x3o3f (-x)3x3f    o3x3f    o3x3f
o3f3o    o3f3o    x3f3o    x3f3o
f3o3o    f3o3o    F3o3o    F3o3o
o3o3x    o3o3x    x3o3x    x3o3x


it might just be CRF this way... it'd be so cool

[Keiji]

Okay, I've been staring at these projections of the D4.4.2 but I'm still not sure what's going on here.

I can see the central hexagon, surrounded by 3 J91s "in front" of it and 3 more "behind". Also, there are two triangular cupolae (one in front and one behind), and six tetrahedra between the J91s.

It looks like there's also two octahedra, one at the very front, one at the very back. Three triangles are joined to J91s and a further triangle is joined to a triangular cupola. But I can't see what the other four triangles are joined to, nor what fills in the gaps between the J91s.

Then on the opposite hemisphere we have this. I can see the central hexagon, with one J92 in front and another behind. I can also see parts of the J91s flattened on the equator since they were highlighted. But I have no idea what all those remaining lacing cells are, nor where the octahedra are.

Any hints? (Maybe a side view? )

[Marek14]

The structure of D4.4.2 is as follows:

6 tetrahedra (reflection symmetry) - joined to 3 bilbiros and 1 triangular cupola
6 square pyramids A (reflection symmetry) - joined to bilbiros through the square face, to two pentagonal pyramids through opposite triangular faces and to one square pyramid B and one tridiminished icosahedron through remaining triangular faces
6 square pyramids B (reflection symmetry) - joined to one thawro through the square face, to two pentagonal pyramids through opposite triangular faces and to one square pyramid A and the remaining thawro through remaining triangular faces
12 pentagonal pyramids (no symmetry) - joined to another pentagonal pyramid through the pentagonal face. The triangular faces join to, in order: square pyramid A, square pyramid B, thawro, tridiminished icosahedron, bilbiro
2 octahedra (3-gonal pyramidal symmetry) - joined to triangular cupola through one triangular face, to 3 bilbiroes through 3 faces adjacent to it, to tridiminished icosahedra through next 3 faces and to thawro through the remaining face.
2 triangular cupolas (3-gonal pyramidal symmetry) - joined to the other triangular cupola through the hexagonal face, to 3 bilbiroes through the square faces, to 3 tetrahedra through the lateral triangle faces and to octahedron through the top triangular face
6 tridiminished icosahedra (reflection symmetry) - joined to 2 bilbiros and 1 thawro through the pentagonal faces, to octahedron through the bottom triangular face, to another bilbiro through the lateral triangular face joined to 2 bilbiro-bearing pentagons, to 2 pentagonal pyramids through the other 2 lateral triangular faces and to square pyramid A through the top triangular face
6 bilbiros (reflection symmetry) - joined to 2 tridiminshed icosahedra through pentagonal faces on one side and to 2 more bilbiros through pentagonal faces on the other side, to square pyramid A and triangular cupola through the square faces. Triangular faces connect to: 2 pentagonal pyramids (luna triangles adjacent to square pyramid A), tetrahedra (luna triangles adjacent to triangular cupola), thawro (rotunda triangle adjacent to square pyramid A and 2 tridiminished icosahedra), octahedron (rotunda triangle adjacent to triangular cupola and 2 tridinimished icosahedra), tetrahedron (rotunda triangle adjacent to triangular cupola and 2 bilbiros) and tridiminished icosahedron (rotunda triangle adjacent to square pyramid A and 2 bilbiros)
2 thawros (3-gonal pyramidal symmetry) - joined to the other thawro through hexagonal face, to 3 tridiminished icosahedra through pentagonal faces, to 3 square pyramids B through square faces. Triangular faces connect to: 3 square pyramids B (the lowest layer), 6 pentagonal pyramids (second layer), 3 bilbros (top layer) and octahedron (top triangle)

So: Gaps between J91's -- they form 2 triplets which surround a triangular cupola and octahedron, with gaps filled by tetrahedra and big gaps between pentagonal faces filled by tridiminished icosahedra.

[quickfur]

The structure of D4.4.2 is as follows:

6 tetrahedra (reflection symmetry) - joined to 3 bilbiros and 1 triangular cupola

I find that this part of the polychoron is the most interesting: it has 3 bilbiros attached to a tetrahedron in a very non-obvious manner. I would never have thought to put cells together in this way, if I were to start constructing it from this position!

[...] So: Gaps between J91's -- they form 2 triplets which surround a triangular cupola and octahedron, with gaps filled by tetrahedra and big gaps between pentagonal faces filled by tridiminished icosahedra.

Yep.