considering the expansions x3o5o"="(-x)3x5o=>bilbiro.
 One part of this expansion looks like (-x)3x5o => o3x5o, and the other part looks like (-x)3x5o => x3o5x. When I tried to understand why it is exactly the expansion (-x)3x5o=>x3o5x, I got stuck, so I went on, just accepting that this happens. Then I got to consider why there is a part of x5o3x3x in the bilbiro'd o5x3o3x.
One part of this expansion looks like (-x)3x5o => o3x5o, and the other part looks like (-x)3x5o => x3o5x. When I tried to understand why it is exactly the expansion (-x)3x5o=>x3o5x, I got stuck, so I went on, just accepting that this happens. Then I got to consider why there is a part of x5o3x3x in the bilbiro'd o5x3o3x. When I considered the expansion o5o3x3o"="o5x3(-x)3x => bilbiro'd o5x3o3x, I saw one part looked like the expansion o5x3(-x)3x => o5x3o3x, and the other part looked like o5x3(-x)3x => x5o3x3x. You can see the similarity with the bilbiro-expansion, yet without any explanation why that happens. (the .5.3.-part is practically identical to the bilbiro'd ike)
The orthocupolarotunda'd ike also has a part going (-x)3x5o=>o3x5o and one part going (-x)3x5o => x3o5x. this also happens in the bilbiroing of o5x3o3x, giving the orthocupolarotunda's.
Then I wanted to see how far this analogy holds, so I went on considering the expansion o5o3o3x "=" o5o3x3(-x) "=" o5x3(-x)3o => bilbiro'd o5x3o3o. This should, if my analogy is correct, have partg going like o5x3(-x)3o=>o5x3o3o, and parts going like o5x3(-x)3o => x5o3x3o. So I went on searching for parts of x5o3x3o in the bilbiro'd o5x3o3o. This isn't directly present, but in analogy of inserting a patch of x5o3x3x in o5x3o3x, I tried to insert a patch of x5o3x3o in o5x3o3o, and it worked (you even have the "missing" parts of the bilbiro's in there). This "patch" is shown when you insert a pentagonal magnabicupolic ring in the decagonal prisms of the bilbiro'd o5x3o3o, such that the squippy's become oct's, and the pentagonal cupolae become orthocupolarotundae. The resulting figure should be considered the "real" bilbiro'd o5x3o3o, and the former figure a diminishing of that.
To make the analogy complete, I tried to find the orthocupolarotundae in the bilbiro'd o5o3x3o. these are present as well (I think), and they can be shown by removing the following vertices:
 you should look at the nearest bilbiro. the penatgon next to the edge of a triangle of the bilbiro (so the pentagon touching the triangle of the bilbiro, but not part of the bilbiro itself)should be deleted, together with the vertex that makes a pentagonal pyramid out of this.
you should look at the nearest bilbiro. the penatgon next to the edge of a triangle of the bilbiro (so the pentagon touching the triangle of the bilbiro, but not part of the bilbiro itself)should be deleted, together with the vertex that makes a pentagonal pyramid out of this. I just made up the stott-deriviation of this bilbiro'd o5o3x3o. o5o3x3o"="o5x3(-x)3x "=" o5x3o3(-x). this should be the product of the o5x3(-x)3A=>o5x3o3A procedure, so A=-x, and the "parent" figure is o5x3(-x)3(-x). this is not "equal" to a uniform CRF, so the stott-deriviation is a bit weird. nevertheless, via analogy, it should also have parts of x5o3x3(-x) "=" x5o3o3x. this is true, it does have a pentagonal orthobicupolic ring, borrowed from x5o3o3x.
so in summary all bilbiro-ings are weird stott-expansions, although "we" (I) don't know why. Also orthocupolarotunda-ing is the same procedure as bilbiro-ing. More complex weird stott-expansions such as D4.11 and thawro-ing are still unexplained as well. Furthermore I think this kind of expansion shouldn't be called "partial", because it's a full, combined expansion of both ike=>id and ike=>x5o3x. I guess I'll stick to "weird" expansions as I don't know any better name. lastly, I don't know what ike=>thawro should be seen as, all analogy's seem to fail. please help me out, I think we've got something important here. If you don't understand something of this post, please tell me, I will explain it as best as I can, in order to work this out

 So you're saying that the 5D 600-cell ursateron is actually flat? So we should remove it from the list of CRF ursatopes?
So you're saying that the 5D 600-cell ursateron is actually flat? So we should remove it from the list of CRF ursatopes? this seems random to me, but I believe it has got something to do with the fact that the change of x only appears in the second layer of the lace pyramid, I just have no idea why
this seems random to me, but I believe it has got something to do with the fact that the change of x only appears in the second layer of the lace pyramid, I just have no idea why 


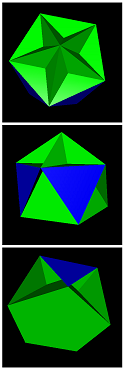
 . Instead, I hope we only have to consider those that have a negative-node representation. e.g. the great dodecahedron can be written as o5x3(-x) "=" o5o3x, and the stellated dodecahedron as f5(-x)3o "=" o5o3x. I'm not able to do such a thing for the great stellated dodecahedron and the great icosahedron, probably because they are based on cuts that are deeper than one edge-length of the convex hull. Anyway, I thought as well this weird stott-expansion/contraction was the grid you were looking for, and that's why I said this might be something important
. Instead, I hope we only have to consider those that have a negative-node representation. e.g. the great dodecahedron can be written as o5x3(-x) "=" o5o3x, and the stellated dodecahedron as f5(-x)3o "=" o5o3x. I'm not able to do such a thing for the great stellated dodecahedron and the great icosahedron, probably because they are based on cuts that are deeper than one edge-length of the convex hull. Anyway, I thought as well this weird stott-expansion/contraction was the grid you were looking for, and that's why I said this might be something important