Marek14 wrote:Hmm... Still looks like there might be a good number of CRFs waiting for discovery.
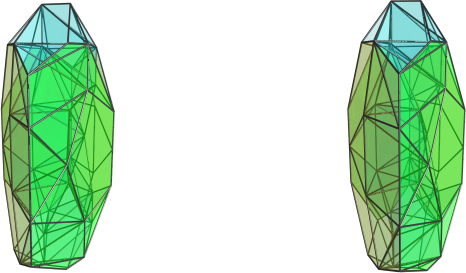
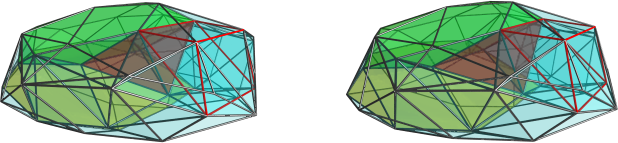
Indeed! Before the discovery of the castellated prism and the J92 crown jewel (anybody has a good name for it yet? it's kinda getting tedious to refer to it as "that thing with 4 J92 cells"

), I was vacillating between thinking there should be a handful of 4D crown jewels, and thinking that maybe there are none because of the increased linking requirements in 4D (in 3D you only had to worry about joining up the edges of regular polygons; in 4D, you have faces in all directions that all must match up to close the shape). But after discovering them, and esp. this last one with a completely unexpected structure, I'm also tempted to think there should be many more out there.
I guess that what we need is a "polychoron builder" application where you could add polychora to faces of existing polychora and "snap" two faces together, foldint the result into 4D, all interactive and graphical

Ah, but the problem with that is that I suck at designing GUIs. Well, actually, I suck at
using GUIs. I find them a great hindrance to what I need to do, so my own polytope programs are all CLI-based. My latest partial rewrite of the main polytope viewer, which is still not completely working, at least has enough functionality now to understand Wendy-style permutation operators and Unicode characters like √, so you can literally input
- Code: Select all
epacs<0, 1, (1+√5)/2>
and it will produce all the vertices of an icosahedron. You can even construct the coordinates piecemeal with the concatenation operator '~':
- Code: Select all
epacs<0, 1, phi> ~ <±1>
produces the icosahedron prism: the epacs applies to the first vector segment, generating the coordinates of an icosahedron, then the concatenation appends <+1> and <-1> to each result. This allows for very convenient algebraic representations of coordinates in my polytope source files, so I can compute convex hulls and render them, and at the same time retain their algebraic formulation for formal mathematical verification of their CRF-ness, etc..
The current (old) version of my polytope viewer has a crude face-lattice querying system, so you can ask for cells that contain faces with 5 vertices, for example, and it will pick up pentagonal pyramids, dodecahedra, etc., but exclude cubes and tetrahedra. It can also filter by visibility (by checking whether the hyperplane normal of a facet faces the current viewpoint). In fact, this query-language is what I use to do almost all my renders when I want to highlight certain cells, or color a group of cells a certain way. Having an explicit scripting language for this means that I can save my renders as script files, so that I can re-create them at any time without needing to click through endless layers of menus, and I can edit them to use precise values (e.g., 1+sqrt(5) instead of 3.23608, which will throw povray off because of roundoff errors and will produce many rendering artifacts.
However, the current query language is rather handicapped, and often I find myself having to manually copy-n-paste intermediate results so that I can later filter them to get what I want (this task is no joke when you're dealing with things like the omnitruncated 120-cell which has 14400 vertices, 28800 edges, and who knows how many more other surtopes). I've been thinking about implementing an improved query language that will run more efficiently (the current implementation is a very inefficient O(n^2) algorithm).
Along with these improvements, I'm thinking of supporting partial polytopes, that is, polytopes that aren't closed up, so they are like cell complexes not necessarily enclosing space. These can be used as "CRFs-in-progress" where you can add/delete cells, snap cells together, etc.. Since I suck at designing/using GUIs, this will probably be script-based, and probably the input would be like a connectivity graph specification, so you can specify graph nodes to be specific polyhedra, then specify how they are to be connected to each other, like "connect cell 0 to cell 1 via ridge 16 with dichoral angle 60°". Probably, some dichoral angles can be replaced with "snap", meaning the program should automatically determine the angle based on adjacent cells. Things like mismatching ridges will generate errors, and there can be commands to check CRF-ness, self-intersection, etc.. Having it in script form also means I can go back and edit an earlier step without needing to redo every subsequent step after making the change, as you'd be forced to with a GUI-based undo/redo function.
Armed with something like this, I'd be able to explore CRFs much more easily, and perhaps even do partially-automated searches (initial part of script specifies a CRF fragment as seed, then give a command for the program to explore all possible CRF extensions up to depth 5 or something, then look at the output for something that looks promising).
At this point, I was thinking mainly about rings of snub square antiprisms...
Hmm... I wonder if you could link those up in a ring! Am I thinking what you're thinking?

Although, I'm a bit worried that perhaps things might not work out, because we got lucky that both J91 and J92 had strong connections to the pentagonal polyhedra, so they fit more easily into the 600-cell framework which is known to work. The snub square antiprism may be much harder to close up in 4D... although if we
do find a CRF with it, that would indicate that maybe
all Johnson solids can occur as cells in CRFs other than just their own prisms! In any case, these may be considered as the "hard crown jewels", as opposed to "soft crown jewels" that are partially derived from existing uniforms/regulars like the 600-cell. They would have structures that are completely unrelated to any known uniforms.




 I suspect something in my toratope threads is also new, but I have no real idea where to look
I suspect something in my toratope threads is also new, but I have no real idea where to look 
 *nudges Klitzing*
*nudges Klitzing*  We could just be the co-authors, and he will do the real work.
We could just be the co-authors, and he will do the real work. 




![Pleased :]](./images/smilies/pleased.gif)

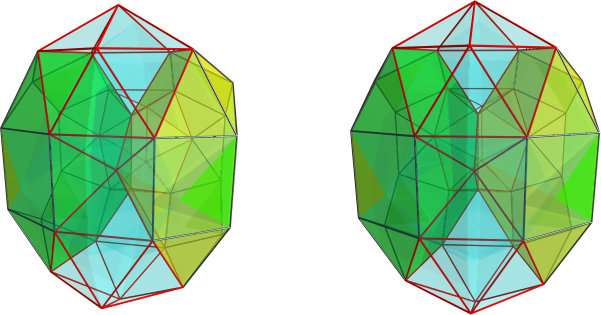
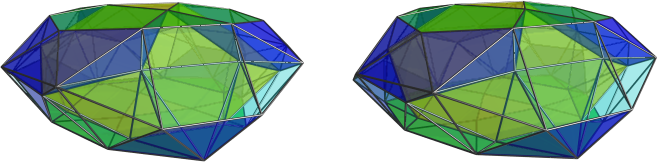





 Unfortunately, that obscures its relation to J92.
Unfortunately, that obscures its relation to J92.