I'll just leave this here, it's now way past my bedtime

student91 wrote:A further investigation of xfox3oxFx3oooo&#xt gave the following:
the first part works out well.
the second part is, according to xfox3oxFx3oooo&#xt, build up by placing a trigonal prism at a triangle of the ....3ox..3oo..&#xt-tetahedron, and then filled up with square pyramids.
The problem here is that [dichoral angle of trigonal prism]+[dichoral angle of square pyramid]=144.7356103<159.0948426=[dichoral angle of J92 at 4.3]. This means it is not possible with a trigonal prism and a square pyramid. you might want to insert a polytope in beween somewhere, it's dihedral angle should then be between 14.3592323 and 56.169471. Of course you could also use different polytopes. fact is that a lot of what is already build is rigid.
student91 wrote:Marek14 wrote:quickfur wrote:Surrounding a tetrahedron is a shard of o5x3o3o. The only other uniform polychoron that uses icosidodecahedra is o5x3o3x.
This would lead into cuboctahedron surrounded by 4 J92's, 4 other cuboctahedra (or possibly triangular cupolas/gyrobicupolas, if those would fit better) and 6 pentagonal prisms. This is a second form that would have to be checked if it can be completed.
What's wrong with putting 4 J92's around a tetrahedron? It would appear that we should be able to at least insert 4 more tetrahedra into the result (i.e. following the pattern of o5x3o3o), which then leaves only the outer surface of hexagons, squares, and triangles, to be closed up. Seems like it should be possible? Or am I missing something obvious?
Well, that was something which was already suggested. My suggestion was meant to be "in addition to", not "in place of" the previous one.
it seems that your polytope is an expansion of mine, so xfox3oxFx3oooo&#xt => xfox3oxFx3xxxx&#xt.
 So the question now is whether the last node is x, or some other quantity. If it's x, then we certainly have a new CRF. But if not, then we'll have to find larger closures for this J92 configuration. Now I'm all tense and expectant, I'm hoping it will work out but I'm not sure.
So the question now is whether the last node is x, or some other quantity. If it's x, then we certainly have a new CRF. But if not, then we'll have to find larger closures for this J92 configuration. Now I'm all tense and expectant, I'm hoping it will work out but I'm not sure. 
 Maybe I'll try to recalculate and see if it's actually 1 after all. The reason I'm somewhat hopeful is because the dihedral angles of the icosidodecahedron are related to the dihedral angles of the tridiminished icosahedron, and the latter has been proven to have CRF results with tetrahedral symmetry. Of course, the non-icosidodecahedral faces of J92 does throw a monkey wrench into the mix, so maybe my hope is ill-founded after all. Hmm.
Maybe I'll try to recalculate and see if it's actually 1 after all. The reason I'm somewhat hopeful is because the dihedral angles of the icosidodecahedron are related to the dihedral angles of the tridiminished icosahedron, and the latter has been proven to have CRF results with tetrahedral symmetry. Of course, the non-icosidodecahedral faces of J92 does throw a monkey wrench into the mix, so maybe my hope is ill-founded after all. Hmm.student91 wrote:That thing is just super awesomely cool.
I mean, ursachora are pretty cool, and this one is like 20 times cooler.
Speaking of which, it has some similarity with ursachora. Ursachora are based on the xfo3oox-buildup of a trid.ike, and this one is based on the xFoFx(2)xofox-buildup of the bilunabirotunda. Therefore, as the ursachora are possible with other symmetries as well, this one might be too, so e.g. xFoFx3ooooo3xofox&#xt might be possible as well, and maybe expanded ones, so xFoFx3xxxxx5xofox&#xt too. I'm not sure about this, and just extrapolated the ursachora to this one. Of course I couldn't've done this extrapolation without your awesome discovery. It's real awesome

student91
Klitzing wrote:student91 wrote:That thing is just super awesomely cool.
I mean, ursachora are pretty cool, and this one is like 20 times cooler.
Speaking of which, it has some similarity with ursachora. Ursachora are based on the xfo3oox-buildup of a trid.ike, and this one is based on the xFoFx(2)xofox-buildup of the bilunabirotunda. Therefore, as the ursachora are possible with other symmetries as well, this one might be too, so e.g. xFoFx3ooooo3xofox&#xt might be possible as well, and maybe expanded ones, so xFoFx3xxxxx5xofox&#xt too. I'm not sure about this, and just extrapolated the ursachora to this one. Of course I couldn't've done this extrapolation without your awesome discovery. It's real awesome

student91
Others symmetries? - hmm I have to think that through...
Stott expansion? - surely is!
That is, the pentagons, so far connecting 2 bilbiroes (bilunabirotundae), now would spread apart, giving place for pips (5-prisms) inbetween. The tets (tetrahedra) likewise get extended to tricues (3-cupulae), the peppies (5-pyramids) become pecues (5-cupolae). Further those bilbiro edges, which connect 2 pentagons, formerly were incident to 5 bilbiroes. But now they would spread apart, giving room for further pips.
 I already gave the cell counts for this Stott expansion, but I missed the pentagonal prisms introduced by the spreading apart of the degree-5 edges. Thanks for giving the right counts!
I already gave the cell counts for this Stott expansion, but I missed the pentagonal prisms introduced by the spreading apart of the degree-5 edges. Thanks for giving the right counts! 
And for sure, the srids (small rhombicosidodecahedra) become grids (great ones).
That is, the cell count of xFoFx3xxxxx5xofox&#xt thus is: 2x grid + 40x tricu + 24x pecu + 30x bilbiro + (60+12)x pip.
If you called the former (contracted) version cool, the expanded one is even cooler! As here there are even more Johnson solids being used, both by types and by total count.
 Unless you're kind enough to do that for me.
Unless you're kind enough to do that for me. 
quickfur wrote:But yeah, I think the trigonal/square versions are not CRF, because the 3 J91's around the vertex are rigid, which in turn fixes the dihedral angle of the triangular faces of the pentagonal pyramids, so they have to be pentagonal pyramids and not tetrahedra or square pyramids, otherwise things won't close up.
Klitzing wrote:quickfur wrote:But yeah, I think the trigonal/square versions are not CRF, because the 3 J91's around the vertex are rigid, which in turn fixes the dihedral angle of the triangular faces of the pentagonal pyramids, so they have to be pentagonal pyramids and not tetrahedra or square pyramids, otherwise things won't close up.
I still have not fully wrangled my mind around those ones. But surely yours is no valide argument!
Note that the pentagon-pentagon edge of bilbro has 3-fold vertices and as such is fixed. Moreover it connects to a triangle. I.e. we have a 3-5-5 acron. This very acron likewise occurs in teddi!
Note also that the dihedral angle at that mentioned edge between the pentagons of bilbiro is given as arccos(1/sqrt(5)) = 63.434949°. That is, neither 3, nor 4, nor 5 of them fill up a full circuit. But it is this very defekt, which is needed to bend into 4D.
--- rk
quickfur wrote:student91 wrote:quickfur wrote:But yeah, I think the trigonal/square versions are not CRF, because the 3 J91's around the vertex are rigid, which in turn fixes the dihedral angle of the triangular faces of the pentagonal pyramids, so they have to be pentagonal pyramids and not tetrahedra or square pyramids, otherwise things won't close up.
Note that the ursachora have similar edges (3 tridiminished icosahedra placed face-to-face, and a pyramid filling the gap). This one also works out.
The difference there is that the number of tridiminished icosahedra around an edge is flexible. Here, the number of J91's around the 5.3.5.3 vertex can only be 3, because otherwise it becomes hyperbolic (the angle of the two pentagons is too wide to fit more than 3 J91's around that vertex). So the dichoral angles between the J91's is fixed, which means that if you continue the pattern of 3 J91's around the 5.3.5.3 vertices, it will eventually form an icosahedral framework of J91's, which means the top/bottom edges will have 5 J91's surrounding it.
Now, it may be possible to have other numbers of J91's around that edge, but it means that you cannot also have the repeating pattern of 3 J91's around the 5.3.5.3 vertices anymore, but you'll need some other arrangement of cells to close the shape up.
Klitzing wrote:[...]
Quickfur, no-one is arguing about an other count at that 3.5.3.5 vertex. That one is indeed fixed. Thus you'll have a shard of 3 bilbroes and 2 tets as larger bilding block. But that one can be used freely I think, just as similar patches of triangles and pentagons not only occur within the icosidodecahedron, but also in bilbro (J91) and thawro (triangular hebesphenorotunda, J92), extending it quite differently.
I also think that this shard has kind a triangular shape, when seen from above. So it might well be suitable to build an icosahedron, an octahedron, or an tetrahedron therefrom. And this is exactly what is under discussion. That is, whether those pentagon-pentagon edges of bilbro might become incident by 3, 4, and/or 5.
 But the problem I see is this: suppose you try to make an octahedron with J91's as the "edges". This will retain the 3 J91's surrounding each 3.5.3.5 vertex, but have degree 4 at the pentagon-pentagon edge. So let's construct the shape piece-by-piece. Say we make the first octahedron face ABC, where A, B, C are J91's. So far so good. Now let's say we want to make the second octahedron face. Topologically, we can do this by adding a 4th J91, D, to ABC, say to the free pentagonal face of A. The problem is, once you attach D to A, it now shares the 3.5.3.5 vertex with A, and so it makes a fixed dichoral angle with A (since otherwise, it will be impossible to add another J91 to the other pentagon of A on the other side of the 3.5.3.5, since that vertex is rigid.) Since A itself is rigid, you cannot just bend the ABC part and the AD part around the pentagon-pentagon edge to make a different angle; the dichoral angles of AB and AD are fixed. This in turn causes each additional J91 you add to the complex to always make the same dichoral angles with the preexisting cells, so eventually it will fold into icosahedral symmetry. There's no degree of freedom here to allow for alternatives, unfortunately.
But the problem I see is this: suppose you try to make an octahedron with J91's as the "edges". This will retain the 3 J91's surrounding each 3.5.3.5 vertex, but have degree 4 at the pentagon-pentagon edge. So let's construct the shape piece-by-piece. Say we make the first octahedron face ABC, where A, B, C are J91's. So far so good. Now let's say we want to make the second octahedron face. Topologically, we can do this by adding a 4th J91, D, to ABC, say to the free pentagonal face of A. The problem is, once you attach D to A, it now shares the 3.5.3.5 vertex with A, and so it makes a fixed dichoral angle with A (since otherwise, it will be impossible to add another J91 to the other pentagon of A on the other side of the 3.5.3.5, since that vertex is rigid.) Since A itself is rigid, you cannot just bend the ABC part and the AD part around the pentagon-pentagon edge to make a different angle; the dichoral angles of AB and AD are fixed. This in turn causes each additional J91 you add to the complex to always make the same dichoral angles with the preexisting cells, so eventually it will fold into icosahedral symmetry. There's no degree of freedom here to allow for alternatives, unfortunately. But it seems clear to me that it's not possible.
But it seems clear to me that it's not possible.
So, let's try the other way round. Asume their existance, and derive how those then would look like.
xAoAx-3-ooooo-P-xoBox-&#xt, with some A=A(P) and B=B(P). And xAoAx-3-xxxxx-P-xoBox-&#xt for sure.
- The contracted version for P=5 was Quickfur's first shot. Cells are: 2x srid + 40x tet + 24x peppy + 30x bilbro.
- The expanded version with P=5 then has cells: 2x grid + 40x tricu + 24x pecu + 30x bilbro + (60+12)x pip.
- The contracted version for P=4 should have for cells: 2x sirco + 16x tet + 12x squippy + 12x bilbro.
- The expanded version with P=4 then should have: 2x girco + 16x tricu + 12x squacu + 12x bilbro + 24x pip + 6x cube.
- The contracted version for P=3 should have for cells: 2x co + (8+8)x tet + 6x bilbro.
- The expanded version with P=3 then should have: 2x toe + (8+8)x tricu + 6x bilbro + 12x pip + 4x trip.
--- rk

Klitzing wrote:[...][...]
- The contracted version for P=5 was Quickfur's first shot. Cells are: 2x srid + 40x tet + 24x peppy + 30x bilbro.
- The expanded version with P=5 then has cells: 2x grid + 40x tricu + 24x pecu + 30x bilbro + (60+12)x pip.

 ). Again, the J91's are seen from a 90° angle so their shape is a bit hard to discern, even though this projection does give you a good idea of the global structure of the polychoron. Next, we do a side-view, as before:
). Again, the J91's are seen from a 90° angle so their shape is a bit hard to discern, even though this projection does give you a good idea of the global structure of the polychoron. Next, we do a side-view, as before:
# The two x5x3x's:
apacs<1, 1, 4*phi+1> ~ <±phi>
epacs<1, phi^3, 3+2*phi> ~ <±phi>
epacs<2, phi^2, phi^4> ~ <±phi>
epacs<phi^2, 3*phi, 2*phi^2> ~ <±phi>
epacs<2*phi, 1+3*phi, 2+phi> ~ <±phi>
# The two o5x3F's:
epacs<0, 3+2*sqrt(5), (3+sqrt(5))/2> ~ <±1>
epacs<1, (5+3*sqrt(5))/2, 3+sqrt(5)> ~ <±1>
epacs<(1+sqrt(5))/2, (7+3*sqrt(5))/2, (5+sqrt(5))/2> ~ <±1>
# The central f5x3o:
epacs<0, (1+sqrt(5))/2, 3+2*sqrt(5)> ~ <0>
epacs<1, 1+sqrt(5), (7+3*sqrt(5))/2> ~ <0>
epacs<(5+sqrt(5))/2, 2+sqrt(5), 3+sqrt(5)> ~ <0>
Klitzing wrote:[...]
So, let's try the other way round. Asume their existance, and derive how those then would look like.
xAoAx-3-ooooo-P-xoBox-&#xt, with some A=A(P) and B=B(P). And xAoAx-3-xxxxx-P-xoBox-&#xt for sure.
- The contracted version for P=5 was Quickfur's first shot. Cells are: 2x srid + 40x tet + 24x peppy + 30x bilbro.
- The expanded version with P=5 then has cells: 2x grid + 40x tricu + 24x pecu + 30x bilbro + (60+12)x pip.
- The contracted version for P=4 should have for cells: 2x sirco + 16x tet + 12x squippy + 12x bilbro.
- The expanded version with P=4 then should have: 2x girco + 16x tricu + 12x squacu + 12x bilbro + 24x pip + 6x cube.
- The contracted version for P=3 should have for cells: 2x co + (8+8)x tet + 6x bilbro.
- The expanded version with P=3 then should have: 2x toe + (8+8)x tricu + 6x bilbro + 12x pip + 4x trip.
--- rk
quickfur wrote:If you can prove me wrong, that will be great, since that means more CRFs.But the problem I see is this: suppose you try to make an octahedron with J91's as the "edges". This will retain the 3 J91's surrounding each 3.5.3.5 vertex, but have degree 4 at the pentagon-pentagon edge. So let's construct the shape piece-by-piece. Say we make the first octahedron face ABC, where A, B, C are J91's. So far so good. Now let's say we want to make the second octahedron face. Topologically, we can do this by adding a 4th J91, D, to ABC, say to the free pentagonal face of A. The problem is, once you attach D to A, it now shares the 3.5.3.5 vertex with A, and so it makes a fixed dichoral angle with A (since otherwise, it will be impossible to add another J91 to the other pentagon of A on the other side of the 3.5.3.5, since that vertex is rigid.) Since A itself is rigid, you cannot just bend the ABC part and the AD part around the pentagon-pentagon edge to make a different angle; the dichoral angles of AB and AD are fixed. This in turn causes each additional J91 you add to the complex to always make the same dichoral angles with the preexisting cells, so eventually it will fold into icosahedral symmetry. There's no degree of freedom here to allow for alternatives, unfortunately.
The situation is analogous to the rhombic triacontahedron. You can't make a closed shape out of configurations of 1:phi rhombuses without causing the shape not to close up. You especially can't make it into octahedral symmetry; the only way that can happen is if you modify the rhombus to 1:√2 instead, then it will close up into octahedral symmetry. The J91's are like 1:phi rhombuses, if you try to put their acute vertices in a non-pentagonal configuration, you won't be able to close up the shape.
You can, of course, insert other stuff in between the J91's, and you will be able to modify the global closure properties, but if you only use J91's to fold around each other, it will always end up with icosahedral symmetry.
If you can prove me wrong, please do; I'd like to have more interesting CRFs than not.But it seems clear to me that it's not possible.
So, let's try the other way round. Asume their existance, and derive how those then would look like.
xAoAx-3-ooooo-P-xoBox-&#xt, with some A=A(P) and B=B(P). And xAoAx-3-xxxxx-P-xoBox-&#xt for sure.
- The contracted version for P=5 was Quickfur's first shot. Cells are: 2x srid + 40x tet + 24x peppy + 30x bilbro.
- The expanded version with P=5 then has cells: 2x grid + 40x tricu + 24x pecu + 30x bilbro + (60+12)x pip.
- The contracted version for P=4 should have for cells: 2x sirco + 16x tet + 12x squippy + 12x bilbro.
- The expanded version with P=4 then should have: 2x girco + 16x tricu + 12x squacu + 12x bilbro + 24x pip + 6x cube.
- The contracted version for P=3 should have for cells: 2x co + (8+8)x tet + 6x bilbro.
- The expanded version with P=3 then should have: 2x toe + (8+8)x tricu + 6x bilbro + 12x pip + 4x trip.
--- rk
If you have coordinates for these, I'll run them through my polytope viewer to prove myself wrong. If such coordinates exist, that is.
student91 wrote:The problem here is that xAoAx(2)xoBox&#xt isn't always a bilbro. this is only the case with Quickfurs thing. It took a while before I was conviced of their nonexistence too. The vertex quickfur is talking about fixes the dihedral angle for the pentagons of the bilbro's. this means that the angle of the to-be-inserted pyramid is also fixed, because the bilbro-bilbro-pyramid edge is rigid, and thus fixed with one imput. It might be possible, however, that something with prism-symmetry is possible. e.g. xFoFx3ooooo2xofox&#xt (not very promising) or xFoFx5ooooo2xofox&#xt. they don't close up very nicely though.
 Nevertheless, it has an extremely interesting structure, and the last bits that aren't CRF have edge lengths that almost admit a CRF modification, so I thought I'd post it here.
Nevertheless, it has an extremely interesting structure, and the last bits that aren't CRF have edge lengths that almost admit a CRF modification, so I thought I'd post it here.
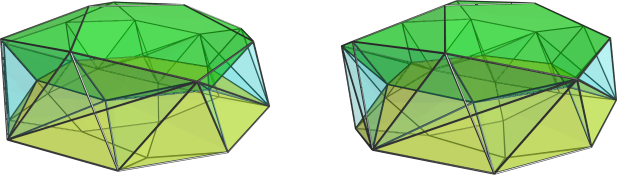

quickfur wrote:[...]
The only remaining edges that are not unit length is exactly φ in length (you can see them between the tips of the respective pentagons of the J92's). These edges are surrounded by tetrahedra that are unit edge length except for one edge that is length φ. Given the tridiminished icosahedra and coincidences involving φ popping up everywhere in the coordinates, my immediate thought was that adding a few more vertices should allow us to replace these scalene tetrahedra with CRF florets of tetrahedra, like in the 600-cell, since the φ edge length suggests that we could break up the edge by "completing the pentagon". But alas, when I calculated the coordinates of the prospective vertices, I found that the points would define a phi-scaled hexagon that lies in the same 2-plane as the hexagon between the two J92's and in the same 3-plane as the J92's, which means that the hexagon will become internal to the polychoron, the square pyramids will disappear, and the J92's merge into non-CRF cells. So close, yet so far!

o3x
x3f
F3o
A3B
x3x o3o
B3A
o3F
f3x
x3o
Klitzing wrote:Still wrong, student91! Quickfiur was not dealing with the 3-5-5 vertex of the bilbiroes, which surely makes that cell rigid within 3D, but tells nothing about its surroundings. He rather was dealing with the 3-5-3-5 vertex of the bilbiroes, which makes the surrounding cells become rigid within 4D, as that one allows in here for 3 bilbiroes and 2 tets only! (Or its Stott expansion ...)
--- rk
student91 wrote:as far as I see it, with the vertices inserted, the lace-city would look somewhat like this:
- Code: Select all
o3x
x3f
F3o
A3B
x3x o3o
B3A
o3F
f3x
x3o
I get stuck at calculating A and B.
But In this picture, you can see that when A and B are calculated, the vertices won't lay in the same plane, and also not in the same 3-space as the J92's. I hope we can get a CRF out of this
[...]
o3o
x3o o3f f3o o3x
o3o o3f f3x x3f f3o o3o
f3o o3F F3o o3f
o3x x3f F3o f3f o3F f3x x3o
f3o o3F F3o o3f
o3o o3f f3x x3f f3o o3o
x3o o3f f3o o3x
o3o
Klitzing wrote:Haha,
consider the hexacosachoron (ex = x3o3o5o) being viewed along a 3-fold axis. The corresponding lace city is
- Code: Select all
o3o
x3o o3f f3o o3x
o3o o3f f3x x3f f3o o3o
f3o o3F F3o o3f
o3x x3f F3o f3f o3F f3x x3o
f3o o3F F3o o3f
o3o o3f f3x x3f f3o o3o
x3o o3f f3o o3x
o3o
You recognize that pattern? In fact it is nothing but the figure shown by "student91" (with the missing numbers A and B already being calculated), multiplied by 6 around the central hexagon. - Really? - Not quite! The central hexagon should have been x3x, not f3f. (But reserve that for later.)
[...]
Now consider that half of id. Reject for a moment the bottom tau scaled hexagon and all those golden polygons (parts of the former pentagons). Then you'll get 6 triangles, each with 2 open sides, the tip of which exactly connecting to the bottom plane. Consider further that those triangles could be spun around the remaining connected side. Then there would be a different angle too, again having the tip connected to the bottom plane. This time they won't point out, rather they would point in. - We could now ask about the pairwise distances of those 6 tips, when bowing to this new constraint. - Well, the answer here is surprisingly simple. They would be spaced at unit distance! In fact, this is how thawro (J92, triangular hebesphenorotunda) is related to id! And yes, those former golden triangles resp. tetragons then become regular ones. And sure, the bottom hexagon thus becomes unit edged too. (Esp. the height of thawros, when measured between the hexagon and the opposite triangle, is exaclty the inradius of id, whith resp. to its triangles.)
 ) that J92 is nothing but a bisected o5x3o, with the 6 equatorial vertices scaled down by phi (conversely, if you scale the hexagonal face of J92 by phi, you'll end up with a bisected o5x3o). So when those tridiminished icosahedra showed up, I immediately recognized it as some kind of diminished 600-cell. But what I wasn't sure about, was whether scaling those equatorial vertices down by phi would maintain CRF-ness in the result, and my initial calculations suggest no. But after student91 kindly provided the lace city for the polychoron, I realized that I've been unconsciously lapsing into 3D-centric thinking again, and so my calculations went in the wrong direction -- in fact, the coplanar coordinates I found were exactly those that turned the J92's back into bisected o5x3o's, which is not what is desired in this case. Nevertheless, on the way to work this morning, I realized that it must be possible to insert two points where the phi-scaled edges are, and get a CRF patch of the 600-cell again.
) that J92 is nothing but a bisected o5x3o, with the 6 equatorial vertices scaled down by phi (conversely, if you scale the hexagonal face of J92 by phi, you'll end up with a bisected o5x3o). So when those tridiminished icosahedra showed up, I immediately recognized it as some kind of diminished 600-cell. But what I wasn't sure about, was whether scaling those equatorial vertices down by phi would maintain CRF-ness in the result, and my initial calculations suggest no. But after student91 kindly provided the lace city for the polychoron, I realized that I've been unconsciously lapsing into 3D-centric thinking again, and so my calculations went in the wrong direction -- in fact, the coplanar coordinates I found were exactly those that turned the J92's back into bisected o5x3o's, which is not what is desired in this case. Nevertheless, on the way to work this morning, I realized that it must be possible to insert two points where the phi-scaled edges are, and get a CRF patch of the 600-cell again.That is, the dissected pentagons of that half of id, represent equatorial sections of rosettes of 5 tets (tetrahedra) of ex. the regular triangles then are bottom faces of other tets. That is, when bending in the triangles around the still connected edge, this represents a bending in of the corresponding tets around the then still connected face. The trapezium deforms into a square. Accordingly that rosette of 5 tets gets replaced by a squippy. And the golden triangle becomes a regular one. That is the other partial rosette of 5 tets becomes replaced by a single tet. That's all. - The remaining structure can be kept. I.e., when finally taking one 6th, you'd re-introduce those so far blended out thawros. You'd get exactly the desired structure!
Thus, finally, this new find of quickfur indeed seems valide. (In fact, that doubted f-edge can be seen from his own renders as being nothing but a false edge, the diagonal of 2 bottom-attached tetrahedra.)
But we not only get this figure now, but a second one for free as well! This is, as quickfur's find in fact is a lune polychoron. As he already pointed out himself, a 60 degree lune. - What about the corresponding 120 degree lune? (Perhaps we might have to fiddle a bit next to the x3x, so. Similar to the n/10-lunes of ex.)
--- rk
Marek14 wrote:Maybe you should publish somewhere about these crown jewels...
student91 wrote:Cool, it exists, and it's extremely awesome.
I still have a little doubt, and I hope you can prove me wrong easilly.
doesn't scaling down the hexagon place the hexagon inside of everything, making it non-convex? I mean, quickfurs program wouldn't've drawn that edge for nothing, or quickfur just told the program to.

Users browsing this forum: No registered users and 49 guests