Johnsonian Polytopes

[quickfur]

[...] But maybe your terminology is more consistent. Would you mind updating the wiki to reflect this change?

Neither know whether I've writing access, nor how to locate all occurancies...
(Thus it might be better, when someone would take hands on, who knows what to do... I might provide some guidance, if required, with respect to the contents.)

You just have to sign up for an account (it's separate from the forum account), and you'll have write access. To my knowledge, the only place where the term 'rotunda' is used is in the CRF polychora project page, maybe a few pages linked from that page. It will probably be helpful to dedicate another page to the terminology, so that we can put in the details/rationale, etc., and link to it from the main CRF page.

I was using the term 'florets' for these polychora, but I guess rosette works just as well, too.

Florets have 2 rings. One clearly is the flower, a rose is an example of. The other is that of a rapier. And that obviously leads into the wrong direction.
[...]

Well, if it's two rings, then we just have to throw duoprism into the mix and it should all work out.

But OK, jokes aside, I guess rosette is a better term.

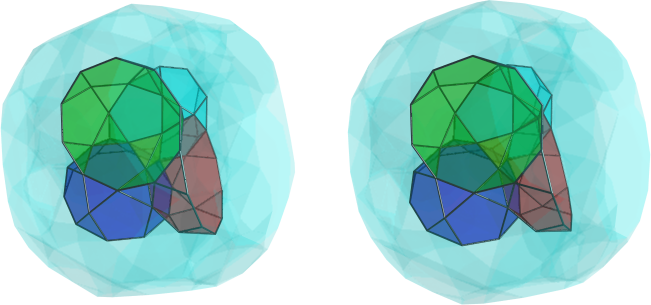
Also, an update on the bicyclodiminishings: it turns out that I did make a mistake -- or rather, there was a bug in one of my utilities that factors coordinates in terms of wendy's apacs/epacs operators, so that 10 vertices failed to be deleted from the original polychoron, thus causing the result to be non-CRF. I decided to bypass the factoring (it was just so the diminishing script I was writing can have nicely-factored forms instead of just a long list of coordinates), and managed to successfully get a CRF polychoron. So, allow me to introduce the bicyclopentadiminished o5x3o3o:



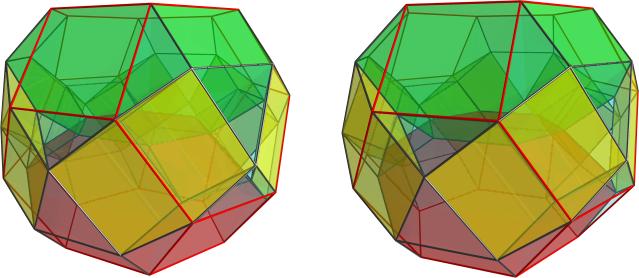
The yellow cells are truncated dodecahedra in one orthogonal ring (only 3 are visible because I left visibility clipping on, but there are 5 in total), and the green cells are truncated dodecahedra in the other orthogonal ring. So we have some kind of 5,5-duoprism symmetry here. Interestingly, the cells in the two rings are bridged by single tetrahedra, with the remaining gaps filled in by a fascinating alternating pattern of pentagonal rotundae plus more tetrahedra in between them. There are 310 cells in total; 10 truncated dodecahedra, 100 pentagonal rotundae, and 200 tetrahedra.

This is wonderful news!! It means that o5x3o3x should also have a bicyclopentadiminishing!

[quickfur]

More views of the bicyclopentadiminished o5x3o3o:

There are several different types of tetrahedra, due to the symmetry-breaking introduced by the diminishings, including one that's completely surrounded by pentagonal rotundae:



Here you see a very interesting chiral tetrahedral configuration of rotundae around the tetrahedron. Is the polychoron itself chiral, though? I'm not sure.

Another interesting fact is that none of the tetrahedral cells share a face with the truncated dodecahedra (though there are a good number that share edges). IOW, the x5xo's are completely surrounded by two other x5xo's, and a bunch of pentagonal rotundae. The following image, this time centering the projection on a decagonal face, shows two of the x4xo's in the same ring, with the 10 rotundae that surround them where they share a decagonal face:



Although not shown, you can see the band around the equator of the projection, where another alternating series of pentagonal rotundae would fit; those are the rotundae surrounding the cells from the orthogonal ring. You can also see the different kinds of tetrahedra here: the chiral one shown above can be seen to fit into the tetrahedral gap between a single magenta rotunda and a single blue rotunda.

[quickfur]

Recently I noticed that Klitzing's paper on segmentochora includes triangular_cupola||tetrahedron and square_cupola||square pyramid, but I couldn't find pentagonal_pyramid||pentagonal_cupola. Does this shape exist? Or is there something about the pentagonal pyramid or pentagonal cupola that makes it impossible to be CRF?

[Klitzing]

Recently I noticed that Klitzing's paper on segmentochora includes triangular_cupola||tetrahedron and square_cupola||square pyramid, but I couldn't find pentagonal_pyramid||pentagonal_cupola. Does this shape exist? Or is there something about the pentagonal pyramid or pentagonal cupola that makes it impossible to be CRF?

For sure, that's an hyperbolic segmentochoron. Just consider peppy being part of ike and pecu being part of srid. Accordingly peppy || pecu has exactly the same height as would have ike || srid. But this one calculates to have a negative squared height (if lacing edges should have unit lengths too)!

--- rk

[quickfur]

Recently I noticed that Klitzing's paper on segmentochora includes triangular_cupola||tetrahedron and square_cupola||square pyramid, but I couldn't find pentagonal_pyramid||pentagonal_cupola. Does this shape exist? Or is there something about the pentagonal pyramid or pentagonal cupola that makes it impossible to be CRF?

For sure, that's an hyperbolic segmentochoron. Just consider peppy being part of ike and pecu being part of srid. Accordingly peppy || pecu has exactly the same height as would have ike || srid. But this one calculates to have a negative squared height (if lacing edges should have unit lengths too)!

--- rk

Thanks for the explanation. I've also realized that it doesn't work because the pentagonal pyramid is too low, so if you have two of them meeting at the apex, then there's not enough space to squeeze in uniform triangular prisms between them -- it would not have unit edge length, or its square faces would have to deform into rhombuses. IOW, the angle defect is negative, so the result cannot be CRF.

[Klitzing]

[...] Here's another line of investigation that I wanted to do, but so far haven't gotten around to: we know the dodecahedra of the 120-cell can be partitioned into 12 great circles of 10 cells each, which gives us a dodecahedral swirlprism sort of arrangement. Now, it should be possible to map each of these great circles to the x5ox's of the x5o3x3o, so that the x5ox's are partitioned into 12 rings. Then within each ring of x5ox's, we can gyrate (resp. cut off) the 10prism||pentagon segmentochora in between the x5ox's, and so we would obtain the swirlgyrated (resp. swirldiminished) x5oxo, which will have 120 parabigyrated x5ox's (resp. parabidiminished x5ox's).

The only thing I'm not sure about, is whether this gyration (resp. diminishing) is CRF, because I'm not sure if the 10p||5g segmentochora from adjacent rings would overlap, making it impossible to gyrate/delete them without making the result non-CRF. Is this possible?

Wow, those are very interesting!

You even could apply that to any such ring individually. Whether such a gyration keeps all angles convex, should be determined. Diminishing clearly would be possible.

As to whether its application to more than 1 ring would lead to intersections of those dips (10p): [...]
Thus it comes out that all these possible swirling diminishings / gyrations should be possible, in any combination btw.: You just have to select a specific swirl orientation first, then you could separately apply cyclo-diminishings and cyclo-gyrations to either ring independently!

Sure the omni-cases would be esp. interesting, as they have the highest symmetry. [...]

And here it comes, the incidence matrix of sidsrahi, the (full-symmetrically) swirl-diminished small rhombihecatonicosachoron:

Code: Select all

1200    *   * |   1    1    1    1    1    0    0 |   1   1   1   1    2    1    1   0 |   2   1   1   1  dip-v with inter dip
   * 1200   * |   0    1    1    1    0    1    1 |   1   1   1   1    1    1    1   1 |   2   1   1   1  dip-v w/o inter dip
   *    * 600 |   0    0    0    0    2    2    2 |   0   1   0   0    2    2    2   2 |   2   0   2   1
--------------+-----------------------------------+------------------------------------+----------------
   2    0   0 | 600    *    *    *    *    *    * |   0   1   0   0    2    0    0   0 |   2   0   1   0  inter dip edges
   1    1   0 |   * 1200    *    *    *    *    * |   1   0   1   0    1    0    1   0 |   1   1   1   1  dip-base edges (inc. to squippy)
   1    1   0 |   *    * 1200    *    *    *    * |   1   1   0   1    0    0    0   0 |   2   1   0   0  dip-base edges (not inc. to squippy)
   1    1   0 |   *    *    * 1200    *    *    * |   0   0   1   1    0    1    0   0 |   1   1   0   1  dip-lacings
   1    0   1 |   *    *    *    * 1200    *    * |   0   0   0   0    1    1    1   0 |   1   0   1   1  squippy lacing (inc. to inter-dip)
   0    1   1 |   *    *    *    *    * 1200    * |   0   0   0   0    0    1    1   1 |   1   0   1   1  squippy lacing (not inc. to inter-dip)
   0    1   1 |   *    *    *    *    *    * 1200 |   0   1   0   0    1    0    0   1 |   2   0   1   0  non-inter-dip trip-lacings
--------------+-----------------------------------+------------------------------------+----------------
   5    5   0 |   0    5    5    0    0    0    0 | 240   *   *   *    *    *    *   * |   1   1   0   0
   2    2   1 |   1    0    2    0    0    0    2 |   * 600   *   *    *    *    *   * |   2   0   0   0
   2    2   0 |   0    2    0    2    0    0    0 |   *   * 600   *    *    *    *   * |   0   1   0   1
   2    2   0 |   0    0    2    2    0    0    0 |   *   *   * 600    *    *    *   * |   1   1   0   0
   2    1   1 |   1    1    0    0    1    0    1 |   *   *   *   * 1200    *    *   * |   1   0   1   0
   1    1   1 |   0    0    0    1    1    1    0 |   *   *   *   *    * 1200    *   * |   1   0   0   1  pabidrid - squippy
   1    1   1 |   0    1    0    0    1    1    0 |   *   *   *   *    *    * 1200   * |   0   0   1   1  trip - squippy
   0    2   2 |   0    0    0    0    0    2    2 |   *   *   *   *    *    *    * 600 |   1   0   1   0
--------------+-----------------------------------+------------------------------------+----------------
  20   20  10 |  10   10   20   10   10   10   20 |   2  10   0   5   10   10    0   5 | 120   *   *   *  pabidrid
  10   10   0 |   0   10   10   10    0    0    0 |   2   0   5   5    0    0    0   0 |   * 120   *   *  dip
   2    2   2 |   1    2    0    0    2    2    2 |   0   0   0   0    2    0    2   1 |   *   * 600   *  trip
   2    2   1 |   0    2    0    2    2    2    0 |   0   0   1   0    0    2    2   0 |   *   *   * 600  squippy

--- rk

[Klitzing]

And here comes the incidence matrix of sgysrahi (the swirl-gyrated srahi):

Code: Select all

600    *    *   * |   2    2    2   0    0    0    0    0    0    0 |   1    4    2    2   0   0   0    0    0    0   0 |   2   2   1   0   0
  * 1200    *   * |   0    1    0   1    1    1    1    1    0    0 |   0    1    1    1   1   1   1    2    1    1   0 |   2   1   1   1   1
  *    * 1200   * |   0    0    1   0    1    1    1    0    1    1 |   0    1    1    1   1   1   1    1    1    1   1 |   2   1   1   1   1
  *    *    * 600 |   0    0    0   0    0    0    0    2    2    2 |   0    0    0    0   1   0   0    2    2    2   2 |   2   0   0   2   1
------------------+-------------------------------------------------+---------------------------------------------------+--------------------
  2    0    0   0 | 600    *    *   *    *    *    *    *    *    * |   1    2    0    0   0   0   0    0    0    0   0 |   2   1   0   0   0
  1    1    0   0 |   * 1200    *   *    *    *    *    *    *    * |   0    1    1    1   0   0   0    0    0    0   0 |   1   1   1   0   0
  1    0    1   0 |   *    * 1200   *    *    *    *    *    *    * |   0    1    1    1   0   0   0    0    0    0   0 |   1   1   1   0   0
  0    2    0   0 |   *    *    * 600    *    *    *    *    *    * |   0    0    0    0   1   0   0    2    0    0   0 |   2   0   0   1   0
  0    1    1   0 |   *    *    *   * 1200    *    *    *    *    * |   0    1    0    0   0   1   0    1    0    1   0 |   1   1   0   1   1
  0    1    1   0 |   *    *    *   *    * 1200    *    *    *    * |   0    0    1    0   1   0   1    0    0    0   0 |   2   0   1   0   0
  0    1    1   0 |   *    *    *   *    *    * 1200    *    *    * |   0    0    0    1   0   1   1    0    1    0   0 |   1   1   1   0   1
  0    1    0   1 |   *    *    *   *    *    *    * 1200    *    * |   0    0    0    0   0   0   0    1    1    1   0 |   1   0   0   1   1
  0    0    1   1 |   *    *    *   *    *    *    *    * 1200    * |   0    0    0    0   0   0   0    0    1    1   1 |   1   0   0   1   1
  0    0    1   1 |   *    *    *   *    *    *    *    *    * 1200 |   0    0    0    0   1   0   0    1    0    0   1 |   2   0   0   1   0
------------------+-------------------------------------------------+---------------------------------------------------+--------------------
  5    0    0   0 |   5    0    0   0    0    0    0    0    0    0 | 120    *    *    *   *   *   *    *    *    *   * |   2   0   0   0   0  gyrated {5}
  2    1    1   0 |   1    1    1   0    1    0    0    0    0    0 |   * 1200    *    *   *   *   *    *    *    *   * |   1   1   0   0   0
  1    1    1   0 |   0    1    1   0    0    1    0    0    0    0 |   *    * 1200    *   *   *   *    *    *    *   * |   1   0   1   0   0
  1    1    1   0 |   0    1    1   0    0    0    1    0    0    0 |   *    *    * 1200   *   *   *    *    *    *   * |   0   1   1   0   0
  0    2    2   1 |   0    0    0   1    0    2    0    0    0    2 |   *    *    *    * 600   *   *    *    *    *   * |   2   0   0   0   0
  0    2    2   0 |   0    0    0   0    2    0    2    0    0    0 |   *    *    *    *   * 600   *    *    *    *   * |   0   1   0   0   1
  0    2    2   0 |   0    0    0   0    0    2    2    0    0    0 |   *    *    *    *   *   * 600    *    *    *   * |   1   0   1   0   0
  0    2    1   1 |   0    0    0   1    1    0    0    1    0    1 |   *    *    *    *   *   *   * 1200    *    *   * |   1   0   0   1   0
  0    1    1   1 |   0    0    0   0    0    0    1    1    1    0 |   *    *    *    *   *   *   *    * 1200    *   * |   1   0   0   0   1
  0    1    1   1 |   0    0    0   0    1    0    0    1    1    0 |   *    *    *    *   *   *   *    *    * 1200   * |   0   0   0   1   1
  0    0    2   2 |   0    0    0   0    0    0    0    0    2    2 |   *    *    *    *   *   *   *    *    *    * 600 |   1   0   0   1   0
------------------+-------------------------------------------------+---------------------------------------------------+--------------------
 10   20   20  10 |  10   10   10  10   10   20   10   10   10   20 |   2   10   10    0  10   0   5   10   10    0   5 | 120   *   *   *   *  pabgyrid</a>
  2    2    2   0 |   1    2    2   0    2    0    2    0    0    0 |   0    2    0    2   0   1   0    0    0    0   0 |   * 600   *   *   *  trip
  1    2    2   0 |   0    2    2   0    0    2    2    0    0    0 |   0    0    2    2   0   0   1    0    0    0   0 |   *   * 600   *   *  squippy
  0    2    2   2 |   0    0    0   1    2    0    0    2    2    2 |   0    0    0    0   0   0   0    2    0    2   1 |   *   *   * 600   *  trip
  0    2    2   1 |   0    0    0   0    2    0    2    2    2    0 |   0    0    0    0   0   1   0    0    2    2   0 |   *   *   *   * 600  squippy

(Convexity here still has to be determined.)

--- rk

[Klitzing]

[...] However, it is possible to have a metatridiminishing, produced by deleting the vertices of three cuboctahedra which are meta to each other. Each diminishing produces a gap that can be filled in by a truncated octahedron; the metatridiminishing (which I believe is a maximal diminishing) produces 3 truncated octahedra that are adjacent to each other, and lie on a great circle. The gaps in between are filled in by an interesting band of interconnected trigonal cupolae and cubes: 18 cupolae and 6 cubes.


[...]

Having spoken of bicyp drahi (bicyclopentadiminished rahi), bicyp disrix (bicyclopentadiminished srix), and cytid srico (cyclotridiminished srico) more recently, that one of your mail from last August then would qualify as cytid rico.

In fact, here is the lace city of rico:

Code: Select all

      o3x   x3x   x3o     
                          
                          
   x3x   u3x   x3u   x3x   
                          
                          
x3o   x3u  oH3Ho  u3x   o3x
                          
                          
   x3x   u3x   x3u   x3x   
                          
                          
      o3x   x3x   x3o     


(Here x represents an edge of length 1, u one of size 2, and H one of size 3. Moreover by "oH3Ho" the concentric compound of o3H and H3o is refered.)

And the corresponding lace city of cyted rico then just is given by

Code: Select all

            x3x           
                           
                           
         u3x   x3u         
                           
                           
      x3u  oH3Ho  u3x     
                           
                           
   x3x   u3x   x3u   x3x   


--- rk

[Marek14]

Question: Do we have any polychoron analogous to bilunabitorunda? I.e. made of non-CRF parts of other polychora?

[quickfur]

Question: Do we have any polychoron analogous to bilunabitorunda? I.e. made of non-CRF parts of other polychora?

I believe wintersolstice and myself have tried various constructions for non-uniform CRFs, but we haven't succeeded in finding anything unique as yet. I've tried to construct a 4D equivalent of the snub disphenoid (by analogy on it being a siamese (bi)octahedron), but the analogy doesn't work.

So, no "crown jewels" yet (except maybe Klitzing's cube||icosahedron).

Anyway, on an unrelated note, thinking on the discovery of bicyclopentadiminished o5x3o3o with 5,5-duoprism symmetry, I realized that this corresponds with a non-adjacent 600-cell diminishing; which means that similar diminishings can be carried out on any 120-cell family uniform polychoron that admits a CRF diminishing.

Furthermore, any 120-cell family uniform polychoron that permits CRF diminishing of adjacent elements corresponding to 600-cell vertices will also admit the bi-24cell-diminishing that produces the bidex (bi-24-diminished 600-cell, 48 tridiminished icosahedra). Of course, in that case they will not be cell-transitive, but they should have similar symmetry, plus they will be chiral.

I think we should go through all of the 120-cell family uniform polychora and catalogue the possibilities.

[quickfur]

P.S. One idea I had, though, was to explore various ways of modifying an icosahedral pyramid to produce pieces that might be usable to construct analogues of the Johnson coronas. We can, for example, substitute square pyramids for some of the tetrahedra and see if it's possible to close up the shape. I've been meaning to try this, but I've been very busy with other things IRL.

[Klitzing]

[...] Anyway, on an unrelated note, thinking on the discovery of bicyclopentadiminished o5x3o3o with 5,5-duoprism symmetry, I realized that this corresponds with a non-adjacent 600-cell diminishing; which means that similar diminishings can be carried out on any 120-cell family uniform polychoron that admits a CRF diminishing.

Furthermore, any 120-cell family uniform polychoron that permits CRF diminishing of adjacent elements corresponding to 600-cell vertices will also admit the bi-24cell-diminishing that produces the bidex (bi-24-diminished 600-cell, 48 tridiminished icosahedra). Of course, in that case they will not be cell-transitive, but they should have similar symmetry, plus they will be chiral.

I think we should go through all of the 120-cell family uniform polychora and catalogue the possibilities.

Seems that you're kind of about 3 month behind your time...
Just confer this post from 2012-12-09, where I started exactly this research not only within this very forum, but even within this very thread.
I then subsequently derived the cell counts and even wrote longuish on how to derive their incidence matrices. All that stuff (including those huge matrices) can be found there.
Finally, in this post of 2013-01-08 I even had summed up the results of that research - esp. for your re-entrance into the forum.

In a different thread Wendy meanwhile also started a related topic, i.e. this thread, extrapolating the sequence {5}, {3,5}, {3,3,5}, onto {3,3,3,5} and their corresponding diminishings. - Sure the latter one is not a polyteron, rather a locally 4D hyperbolic tiling. - BTW. Wendy derived those figures only by extrapolating analogy. I struggled to get feeds onto the ground, contacted several persons in this forum and privately. But I have to admit, that there I've not made any progress so far...

--- rk

[quickfur]

[...] Anyway, on an unrelated note, thinking on the discovery of bicyclopentadiminished o5x3o3o with 5,5-duoprism symmetry, I realized that this corresponds with a non-adjacent 600-cell diminishing; which means that similar diminishings can be carried out on any 120-cell family uniform polychoron that admits a CRF diminishing.

Furthermore, any 120-cell family uniform polychoron that permits CRF diminishing of adjacent elements corresponding to 600-cell vertices will also admit the bi-24cell-diminishing that produces the bidex (bi-24-diminished 600-cell, 48 tridiminished icosahedra). Of course, in that case they will not be cell-transitive, but they should have similar symmetry, plus they will be chiral.

I think we should go through all of the 120-cell family uniform polychora and catalogue the possibilities.

Seems that you're kind of about 3 month behind your time...
Just confer this post from 2012-12-09, where I started exactly this research not only within this very forum, but even within this very thread.
I then subsequently derived the cell counts and even wrote longuish on how to derive their incidence matrices. All that stuff (including those huge matrices) can be found there.
Finally, in this post of 2013-01-08 I even had summed up the results of that research - esp. for your re-entrance into the forum.

Yes, but did you consider diminishings with 5,5-duoprism subsymmetry?

In a different thread Wendy meanwhile also started a related topic, i.e. this thread, extrapolating the sequence {5}, {3,5}, {3,3,5}, onto {3,3,3,5} and their corresponding diminishings. - Sure the latter one is not a polyteron, rather a locally 4D hyperbolic tiling. - BTW. Wendy derived those figures only by extrapolating analogy. I struggled to get feeds onto the ground, contacted several persons in this forum and privately. But I have to admit, that there I've not made any progress so far... [...]

I'm afraid my 4D visualization skills are still limited only to euclidean space. Hyperbolic 4D tilings are a bit beyond me, I'm afraid.

[Marek14]

I think that to investigate cuts of 4D hyperbolic tilings properly, we'd first need to investigate possible facets of their vertex figures.

And that's hard to do by hand and imagination. One possibility would be to find all possible hyperplanes that pass through 4+ vertices of the vertex figure, then compute their intersections with it. If they don't intersect any edges outside of vertices (not sure what would happen if they did, but presumably it wouldn't result in a nice shape), you find a polychoron whose vertex figure corresponds to the cut.

My exploration of polychoron cuts was generally based on similar approach, but it's much harder in 4D since the number of vertices involved can huge and there's always a possibility that one of many possible 600-cell facets will have the properties we seek.

Hmm, a program seems to be the best solution here...

[Klitzing]

I think that to investigate cuts of 4D hyperbolic tilings properly, we'd first need to investigate possible facets of their vertex figures.
...

She was quite explicite there:

You can inscribe a tau-scaled chiral compound of 5 icoes into ex. You can diminish ex according to the vertex positions of any number of these icoes. Let's extend the bidex acronym for that purpose:

• then sadi would be nothing but idex,
• then there is bidex itself,
• then there would be tridex,
• quidex,
• and finally, when according to all 5 icoes the diminishing takes place, we would come out with the kernel hi.

• Sure sadi is still uniform and uses 2 facets,
• bidex is only scaliform, but uses only one cell, which is the vertex figure of sadi.
• Tridex would again be noble, using the vertex figure of bidex for cells, and thus is no longer CRF - convex for sure, but no longer unit edges only. It further comes out that tridex is nothing but the dual of bidex.
• And quidex would be the dual of sadi, i.e. having 2 types of vertices, but a single facet type.
• And, as is well-known, hi is the dual of ex.

Wendy just extended that relational sequence then to 3335.

• I.e. id.3335 (here representing: incomplete diminishing) would use ex for additional cells (bottom of chopped off vertex pyramids) and vertex figure should be sadi.
• bid.3335 should use sadis only for cells and bidex for vertex figure.
• tid.3335 should then use bidex for cells only and tridex for vertex figure; it therefore would be self-dual.
• quid.3335 then uses tridex for cells only and quidex for vertex figure; it would be dual to bid.3335.
• pid.3335 then uses quidex for cells only but would have 2 vertex types, the shallower one would have hi for vertex figure; that one should be dual to id.3335.
• And finally there would be 5333, the dual of 3335.

Note, just as this short recapitulation of Wendy's thoughts shows, this is a mere application of analogy. This is no proof of existance. We both already tried to set up incidence matrices for those. But so far we didn't succeed. So either we haven't tried hard enough, or there is some un-seen point which makes their existance impossible.
This is what remains to be evaluated.

Lower dimensional analogy works: i.e. for {5} it is trivial (e.g. inscribed golden triangle) and for {3,5} also known (teddi, Andrew's hexahedron, and dual of teddi). In fact the {5} would be divided into vertices of type ababc. And for ike we would use a face-center inscribed chiral compound of 5 tets, each using 4 colors for vertices.

If analogy would be shown to work for 3335, we even could step up and consider 33335 next, etc.

(Sure, true contributions to that theme most probably would be better to be placed in her thread...)

--- rk

[wendy]

Here's a little secret on hyperbolic geometry.

If all of the points of a polytope lie on the same sphere in one geometry, they do in all geometries that support that curvature. Moreover, such a sphere does not loose its internal geometry when moved from one kind of space to another.

So, for example, the hyperbolic planes that strike a given sphere, create circles, these circles are exactly the same as euclidean planes striking the same sphere. So, if you know that a given plane crosses points x,y,z in euclidean geometry, then there is a same plane striking the sphere in hyperbolic geometry in the same way. This is the secret of 'circle drawing' and the 'polytope projection' that i devised hyperbolic geometry on.

[Klitzing]

Coming back to the main topic of this thread

Having found today a CRF with

• 4 esquidpies (elongated square dipyramids)
• 4 squobcues (square orthobicupolae)
• 16 octs (octahedra)
• 16 trips (trigonal prisms)

Anyone has seen that one before?

Well, here is how to derive it:
Start with sodip (square-octagon duoprism). Augment each alternate cube by cubpies (cube-pyramids) and all ops (octagonal prisms) by {4} || op segmentochora. - So far this sound un-spectacular. But it comes out, that those squippies (square pyramids) of those cubpies either recombine pairwise into octs (octahedra) or unite with the remaining cubes into esquidpies (elongated square dipyramids). Furthermore the squacues of {4} || op likewise combine pairwise into squobcues (square orthobicupolae).

Even then it sounds kind of arbitrary. There are so many duoprism augmentations, even when using pyramids only. So what is special in here?

It further comes out, that this finding also can be obtained as a partial Stott contraction of srit (small rhombated tesseract)! Consider srit as tristratic polychoron, omit the central ticcup (truncated-cube prism) and recombine the outer parts into an orthobicupola. Then take this and apply the same procedure in an orthogonal direction again.

This construction esp. proves both, the overall convexity and the recombination of corealmic parts: octs clearly are already contained in srit. And for the occurance of those Johnsonian solids just consider the restriction of that action onto the sircoes (snall rhombicuboctahedra) of srit: One subset of 4 then gets its central stratos (ops) omitted, the other one gets this operation being applied twice.

What is meant here can be made evident, when considering the lace cities of srit ...

Code: Select all

x4o x4x   x4x x4o
                
x4x w4o   w4o x4x
                
                
x4x w4o   w4o x4x
                
x4o x4x   x4x x4o


... and of my new finding (in fact, this was how I first came across):

Code: Select all

x4o x4x x4o
          
x4x w4o x4x
          
x4o x4x x4o


Thus it becomes a relative to the last-year finding of quickfur, which meanwhile has been called quawros (quadratic wedge rosette), which likewise can be derived as a partial Stott contraction, here from sidpith (small disprismatotesseractihexadecachoron).

I even have thought about naming that new fellow. I think it is best described as bicyclotetraugmented sodip, therefore as OBSA we could use bicyte ausodip. (@hedrondude )

--- rk

[Klitzing]

next partial Stott contraction:

this time applied to prit (prismatorhombitesseract)

Code: Select all

    x4o x4x   x4x x4o          = x3o4x
                         
x4o     x4u   x4u     x4o      = u3o4x
                         
x4x x4u w4x   w4x x4u x4x      = x3x4x
                         
                         
x4x x4u w4x   w4x x4u x4x
                         
x4o     x4u   x4u     x4o
                         
    x4o x4x   x4x x4o   


and getting:

Code: Select all

    x4o x4x x4o          = xxx4oxo&#xt

x4o     x4u     x4o      = xxx4ouo&#ut

x4x x4u w4x x4u x4x      = xxwxx4xuxux&#xt

x4o     x4u     x4o

    x4o x4x x4o   


That one uses 4 squobcues (square orthobicupolae), 4 cubes, 16 hips (hexagonal prisms), 16 tuts (truncated tetrahedra), and 4 esquidpies (elongated square dipyramids).

Any idea how to name that one?

--- rk

[Marek14]

Well, since this shape is basically made by removing the middle layers, the innards of polychoron, how about eviscerated prit?

[Klitzing]

That recent finding is part of a more general observation.

(In the followings I use Wendys abbreviations for edge lengths:

Code: Select all

o = zero length edge (point)
x = unit edge
q = edge of size sq2
u = edge of size 2
w = edge of size 1+sq2)

Consider first 3D:

Here we have

A) x3o4x (sirco)
as lace city:

Code: Select all

  x x   
x w w x
x w w x
  x x   

A1) That one can be reduced in 1 coordinate direction into: squobcu
as lace city:

Code: Select all

  o o   
o q q o
o q q o
  o o   

or in different orientation:

Code: Select all

  x x   
x w w x
  x x   

A2) Reduction in 2 orthogonal directions results in: esquidpy
as lace city:

Code: Select all

  o o   
o q q o
  o o   

or in different orientation:

Code: Select all

  x   
x w x
  x   

A3) Full reduction (all 3 directions) results in: x3o4o (oct)
as lace city:

Code: Select all

  o   
o q o
  o   

Or start with
B) o3o4x (cube)
as lace city:

Code: Select all

x x
x x

B1) That one can be reduced in 1 coordinate direction into: {4}
as lace city:

Code: Select all

o o
o o

or in different orientation:

Code: Select all

x x

B2) Reduction in 2 orthogonal directions results in: edge
as lace city:

Code: Select all

o o

or in different orientation:

Code: Select all

x

B3) Full reduction (all 3 directions) results in: o3o4o (point)
as lace city:

Code: Select all

o

Now move on to 4D:

C) x3x3o4x (prit)
as lace city:

Code: Select all

    x4o x4x   x4x x4o     
                         
x4o     x4u   x4u     x4o
                         
x4x x4u w4x   w4x x4u x4x
                         
                         
x4x x4u w4x   w4x x4u x4x
                         
x4o     x4u   x4u     x4o
                         
    x4o x4x   x4x x4o     

C2) Reduction in 2 orthogonal directions results in: (no name so far)
as lace city:

Code: Select all

    x4o x4x x4o     
                   
x4o     x4u     x4o
                   
x4x x4u w4x x4u x4x
                   
x4o     x4u     x4o
                   
    x4o x4x x4o     

or in different orientation:

Code: Select all

    o4o o4x   o4x o4o     
                         
o4o     o4u   o4u     o4o
                         
o4x o4u q4x   q4x o4u o4x
                         
                         
o4x o4u q4x   q4x o4u o4x
                         
o4o     o4u   o4u     o4o
                         
    o4o o4x   o4x o4o     

C4) Full reduction (all 4 directions) results in: x3x3o4o (thex)
as lace city:

Code: Select all

    o4o o4x o4o     
                   
o4o     o4u     o4o
                   
o4x o4u o4x o4u o4x
                   
o4o     o4u     o4o
                   
    o4o o4x o4o     

D) x3o3o4x (sidpith)
as lace city:

Code: Select all

    x4o   x4o     
                 
x4o x4x   x4x x4o
                 
                 
x4o x4x   x4x x4o
                 
    x4o   x4o     

D2) Reduction in 2 orthogonal directions results in: quawros
as lace city:

Code: Select all

    x4o     
           
x4o x4x x4o
           
    x4o     

or in different orientation:

Code: Select all

    o4o   o4o     
                 
o4o o4x   o4x o4o
                 
                 
o4o o4x   o4x o4o
                 
    o4o   o4o     

D4) Full reduction (all 4 directions) results in: x3o3o4o (hex)
as lace city:

Code: Select all

    o4o     
           
o4o o4x o4o
           
    o4o     

E) o3x3o4x (srit)
as lace city:

Code: Select all

x4o x4x   x4x x4x
                 
x4x w4o   w4o x4x
                 
                 
x4x w4o   w4o x4x
                 
x4o x4x   x4x x4o

E2) Reduction in 2 orthogonal directions results in: bicyte ausodip
as lace city:

Code: Select all

x4o x4x x4x
           
x4x w4o x4x
           
x4o x4x x4o

or in different orientation:

Code: Select all

o4o o4x   o4x o4x
                 
o4x q4o   q4o o4x
                 
                 
o4x q4o   q4o o4x
                 
o4o o4x   o4x o4o

E4) Full reduction (all 4 directions) results in: o3x3o4o (ico)
as lace city:

Code: Select all

o4o o4x o4x
           
o4x q4o o4x
           
o4o o4x o4o

F) o3o3o4x (tes)
as lace city:

Code: Select all

x4o   x4o
         
         
x4o   x4o

F2) Reduction in 2 orthogonal directions results in: {4}
as lace city:

Code: Select all

o4o   o4o
         
         
o4o   o4o

or in different orientation:

Code: Select all

x4o

F4) Full reduction (all 4 directions) results in: o3o3o4o (point)
as lace city:

Code: Select all

o4o

NB:

• In cases C, ..., F the ..1 and ..3 cases clearly would exist too, just too trivial to display additionally. (And to be named, I fear.)
• quawros (quadratic wedge rosette) last year was found by quickfur. All other 4D ones were discovered by myself (at least I'm not aware of other mentions).
• In this context however they seem to belong to a more general concept.
• Thus we should consider a specific naming concept. So far I use "partial Stott contraction" as a working title. Hedrondude already suggested "condensed". Marek14 suggested "eviscerated". - Both are appreceated, but seem to be understandable only from context, not by their own. - Any further ideas? (This should be solved first, before asking for a name for that TBD C2) case.)
• It obviously comes out, that this procedure quite generally applies to any decoration of o3o...o3o4o, provided that the last node bears an "x" and the one but last remains an "o".
• So far it is not apparent to me, whether this could be extended to other symmetries as well.

--- rk

[quickfur]

Been busy the last little while, so only caught up today (and only skimmed over your new ideas, klitzing, I still have to come back to re-read it in detail later). I like "partial Stott contraction", so maybe "contracted polytopes"? Although, that may have the wrong connotation (like contracting germs ). Depending on how many axis we contract, we can write 1-contracted, 2-contracted, etc..

As for generalization to other symmetries, I'm not so sure, it seems difficult because n-cube symmetry is the only one with trivial dissection properties (i.e. an n-cube can be cut into smaller n-cubes evenly, which also allows trivial elongations, partial Stott expansions/contractions, etc.). One possible direction to look, though, might be the duoprisms. There, the regularity of the toroidal ridge between the two rings (consisting of a grid of squares) may make it easier to perform partial expansions, maybe? One can also look into "inflating" the rings apart so that they no longer touch each other, and filling in the gaps with CRFs (something like the grand antiprism, but not necessarily with tetrahedra -- what about square pyramids, say?).

If this approach proves fruitful, we can also consider its generalization to other swirlprism symmetries: take the bidex, for example: is it possible to pull the 8 rings apart (maybe by inserting prisms, or expanding the cells somehow along the ring but leave new gaps at the interfaces between rings) and insert CRF polyhedra to fill in the gaps? I think it's safe to say that at least some such expansion is possible -- in the form of a 24-diminishing of the other 120-cell uniforms. Are there expansions which are not directly derived from a 120-cell uniform diminishing, though?

Also, I've been thinking about searching for CRFs with swirlprism symmetry, that are not directly derivable from the uniforms. Any thoughts/ideas?

[Klitzing]

Been busy the last little while, so only caught up today (and only skimmed over your new ideas, klitzing, I still have to come back to re-read it in detail later). ...

My last mail was the essence of the former ones

... I like "partial Stott contraction", ...

Yep, this is in fact what those are. It was Alicia Boole Stotts term, contraction, the opposite operation of expansion. - Sure, she didn't apply it as partial operations to be applied in different directions, rather as an operation to be applied globaly to all equivalent elements. So it turns out that it is kind a completely new idea, even so it comes out to be, if applied to all directions at the same time (or even one by one) that the result would look like Alicias contraction.

... so maybe "contracted polytopes"? Although, that may have the wrong connotation (like contracting germs ). Depending on how many axis we contract, we can write 1-contracted, 2-contracted, etc.. ...

Possible, but on the one hand this would not un-umbiguously connote how thick the medial to be omitted segment would be, and on the other that very number even could be miss-interpreted as just giving that thickness (instead of the number of directions).

... As for generalization to other symmetries, I'm not so sure, it seems difficult because n-cube symmetry is the only one with trivial dissection properties (i.e. an n-cube can be cut into smaller n-cubes evenly, which also allows trivial elongations, partial Stott expansions/contractions, etc.). One possible direction to look, though, might be the duoprisms. There, the regularity of the toroidal ridge between the two rings (consisting of a grid of squares) may make it easier to perform partial expansions, maybe? One can also look into "inflating" the rings apart so that they no longer touch each other, and filling in the gaps with CRFs (something like the grand antiprism, but not necessarily with tetrahedra -- what about square pyramids, say?). ...

One has to bear in mind that an essential ingrediant in those shown possible cases for partial Stott contractions is that no other 2D-faces other than squares are contracted, that is, the equatorial segment has to be a true prism (independent of those prismatic parts are themselves complete or in turn equatorial parts of larger cells).

While writing this, it occurs to me that we might consider a term like "de-prismation"? One the other hand, "depri" also has different connotations, haha.

... If this approach proves fruitful, we can also consider its generalization to other swirlprism symmetries: take the bidex, for example: is it possible to pull the 8 rings apart (maybe by inserting prisms, or expanding the cells somehow along the ring but leave new gaps at the interfaces between rings) and insert CRF polyhedra to fill in the gaps? ...

In general this does not work. the thereby required angles would not allow for CRF-polyhedral cells.

... I think it's safe to say that at least some such expansion is possible -- in the form of a 24-diminishing of the other 120-cell uniforms. ...

Those were already described in earlier posts of mine.

... Are there expansions which are not directly derived from a 120-cell uniform diminishing, though? ...

Hmmm, don't know whether I get completely what you bear in mind here. With respect to Stott expansions at least, the answer probably is "no". Alicias expansions seem to be exactly equivalent to the Wythoff constructions and so would not go beyond uniform ones.

... Also, I've been thinking about searching for CRFs with swirlprism symmetry, that are not directly derivable from the uniforms. Any thoughts/ideas?

Up to my knowledge so far nothing is known here.

--- rk

[Klitzing]

... One has to bear in mind that an essential ingrediant in those shown possible cases for partial Stott contractions is that no other 2D-faces other than squares are contracted, that is, the equatorial segment has to be a true prism (independent of those prismatic parts are themselves complete or in turn equatorial parts of larger cells).

While writing this, it occurs to me that we might consider a term like "de-prismation"? One the other hand, "depri" also has different connotations, haha. ...

I've found other cases too, where this "deprismation" would apply, but when applyng to reduction-parallel equatorial hexagons those would reduce to 60°/120° rhombs and when applying to octagons you'd get 90°/135° hexagons, i.e. no longer remaining in the CRF class. (Easy 3D examples: omit the equatorial part of tic (being oriented {8} first), or that of a toe (being oriented with its {6}-{6}-edge first).)

--- rk

[Klitzing]

... As for generalization to other symmetries, I'm not so sure, it seems difficult because n-cube symmetry is the only one with trivial dissection properties (i.e. an n-cube can be cut into smaller n-cubes evenly, which also allows trivial elongations, partial Stott expansions/contractions, etc.). One possible direction to look, though, might be the duoprisms. There, the regularity of the toroidal ridge between the two rings (consisting of a grid of squares) may make it easier to perform partial expansions, maybe? One can also look into "inflating" the rings apart so that they no longer touch each other, and filling in the gaps with CRFs (something like the grand antiprism, but not necessarily with tetrahedra -- what about square pyramids, say?). ...

One has to bear in mind that an essential ingrediant in those shown possible cases for partial Stott contractions is that no other 2D-faces other than squares are contracted, that is, the equatorial segment has to be a true prism (independent of those prismatic parts are themselves complete or in turn equatorial parts of larger cells).

While writing this, it occurs to me that we might consider a term like "de-prismation"? One the other hand, "depri" also has different connotations, haha. ...

Thought a little. - Found more!

Consider the 3D case again first. We have got so far the following sequences

• point -> edge -> square -> cube
• oct -> esquidpy -> squobcu -> sirco

Those sequences use partial Stott expansions in dihedral subsymmetry each, subsequently applied to mutually orthogonal directions.

But there is more!
Consider the sequences

• oct -> tut -> toe
• trip -> hip

Here the first one applies partial Stott expansion onto tetrahedral subsymmetry, while the second applies it onto trigonal subsymmetry.

Now step up to 4D.
Consider the ico (24-cell). We will consider that expansion, which finally would end in tico (truncated ico). But we will do that in partial steps here. This one turns out not to be a new one. This is because of its embedding into demihedral subsymmetry:

• ico = x3o4o3o = o3x3o4o = o3x3o *b3o (this latter tristar Dynkin symbol will make it obvious)
  Each "arm" would represent a subset of 8 octahedra, in fact, one for each hexadecachoron, which could be vertex inscribed into the icositetrachoron. And note moreover that the latter is selfdual, that is, those hexadecachora could well be oriented to point to the centers of the octs.
  
• Thus the first partial expansion will choose one such subset of 8 octahedra and pull those apart. Then the remaining 2*8 octs get deformed into tuts - and the former 24 connection points (of those chosen octs) become new edges. - The result figur would be the well-known thex = x3x3o4o = x3x3o *b3o.
  
• Next choose a further inscribed hexadecachoron, i.e. a subset of 8 of those tuts, and apply the (partial) Stott expansion to pull those apart. Then those 8 tuts clearly remain tuts. The other 8 tuts become toes, and the priviously remaining octs become tuts instead. And those 24 new edges now become squares. - The result will be nothing but tah = o3x3x4o = x3x3x *b3o.
  
• Finally consider the 8 toes of tah, and apply a partial Stott expansion here, pulling those apart. This clearly deforms the 2*8 tuts into toes as well. And those special squares now become cubes. - This now is tico = x3x4o3o = x3x3x4o = x3x3x *b3x.

Note, that the dihedral partial Stott expansions (resp. contractions when applied the other way round) re-occur in here too.

That sequence was not new, as I mentioned. But there is a similar application, resulting in non-uniform intermedial steps:

• Consider spic = x3o4o3x as starting figure. That one uses both set of octs of the dual pair of icoes.
• Again choose a similar set of 8 octs and pull those apart. Where in the former case were connection points here ore the 24 octs of the dual ico. Those thus become elongated into esqidpies. the remaining 2*8 octs again become tuts. Further one subset of 32 trips becomes deformed into hips, while the remaining 5*32 remain trips. - This figure btw. is an already known CRF: quickfur last year has found it independently as being an octa-augmented prit.
  
• Next choose one of the subsets of 8 tuts, and pull them apart. Those clearly will remain tuts. The 8 remaining octs now will become tuts as well. The former other tuts become toes. And the esquidpies become squobcues. The hips remain hips. One further subset of 32 trips likewise becomes hips. Thus 4*32 of the trips remain. - This figure so far was never described (to my knowledge)!
• Finally pull those 8 toes apart. The 2*8 tuts then become toes as well. The squobcu become sircoes. Further 32 trips become hips, while the former hips remain, as do the other 3*32 trips. - This then will be nothing but prico = x3x4o3x.

Thus "(de-)prismation" after all would not serve any longer. We have to come back to "partial Stott expansin/contraction".

--- rk

[Klitzing]

• ico = x3o4o3o = o3x3o4o = o3x3o *b3o (this latter tristar Dynkin symbol will make it obvious)
  Each "arm" would represent a subset of 8 octahedra, in fact, one for each hexadecachoron, which could be vertex inscribed into the icositetrachoron. And note moreover that the latter is selfdual, that is, those hexadecachora could well be oriented to point to the centers of the octs.
  
• Thus the first partial expansion will choose one such subset of 8 octahedra and pull those apart. Then the remaining 2*8 octs get deformed into tuts - and the former 24 connection points (of those chosen octs) become new edges. - The result figur would be the well-known thex = x3x3o4o = x3x3o *b3o.
  
• Next choose a further inscribed hexadecachoron, i.e. a subset of 8 of those tuts, and apply the (partial) Stott expansion to pull those apart. Then those 8 tuts clearly remain tuts. The other 8 tuts become toes, and the priviously remaining octs become tuts instead. And those 24 new edges now become squares. - The result will be nothing but tah = o3x3x4o = x3x3x *b3o.
  
• Finally consider the 8 toes of tah, and apply a partial Stott expansion here, pulling those apart. This clearly deforms the 2*8 tuts into toes as well. And those special squares now become cubes. - This now is tico = x3x4o3o = x3x3x4o = x3x3x *b3x.

Note that this sequence can both be considered a partial Stott expansion sequence and a classical one!
This is due to different symmetries of reference:

Either you consider the full icositetrachoral one, then it becomes a partial one:

Code: Select all

x3o4o3o = ico <--> thex <--> tah <--> x3x4o3o = tico

Alternatively you just consider demitesseractic symmetry, then it becomes a classical one:

Code: Select all

o3x3o *b3o = ico <--> x3x3o *b3o = thex <--> x3x3x *b3o = tah <--> x3x3x *b3x = tico

The relevant cell counts respectively cell transitions here are

Code: Select all

   ico   thex   tah    tico
8  oct   oct    tut    toe
8  oct   tut    tut    toe
8  oct   tut    toe    toe
24 point edge   square cube


• Consider spic = x3o4o3x as starting figure. That one uses both set of octs of the dual pair of icoes.
• Again choose a similar set of 8 octs and pull those apart. Where in the former case were connection points here ore the 24 octs of the dual ico. Those thus become elongated into esqidpies. the remaining 2*8 octs again become tuts. Further one subset of 32 trips becomes deformed into hips, while the remaining 5*32 remain trips. - This figure btw. is an already known CRF: quickfur last year has found it independently as being an octa-augmented prit. [...]
• Next choose one of the subsets of 8 tuts, and pull them apart. Those clearly will remain tuts. The 8 remaining octs now will become tuts as well. The former other tuts become toes. And the esquidpies become squobcues. The hips remain hips. One further subset of 32 trips likewise becomes hips. Thus 4*32 of the trips remain. - This figure so far was never described (to my knowledge)!
• Finally pull those 8 toes apart. The 2*8 tuts then become toes as well. The squobcu become sircoes. Further 32 trips become hips, while the former hips remain, as do the other 3*32 trips. - This then will be nothing but prico = x3x4o3x.

In this 2nd sequence case, there clearly is no alternate view. Those polychora cannot be written as closed Dynkin symbols of demitesseractic symmetry. Therefore it is forced to be a partial Stott expansion / contraction sequence! (I.e. again surpassing Alicia's 1913 intend - exactly 100 years after, hehe.)

Here the relative cell counts respectively cell transitions are

Code: Select all

   spic  owau  (no    prico
         prit  name)
8  oct   oct   tut    toe
8  oct   tut   tut    toe
8  oct   tut   toe    toe
24 oct   esqu. squob. sirco
32 trip  trip  trip   hip
32 trip  trip  hip    hip
32 trip  hip   hip    hip
96 trip  trip  trip   trip


Reading that sequence from the left, we might re-name owau prit (octa-augmented prismatorhombated tesseract) also a pox spic (partially octa-expanded small prismated (dis)icositetrachoron), and then that un-named one a phex spic (partially hexadeca-expanded small prismated (dis)icositetrachoron).

Reading the sequence from the right, we well could name that "un-named one" a poc prico (partially octa-contracted prismatorhombated icositetrachoron), and then that owau prit correspondingly a phic prico (partially hexadeca-contracted prismatorhombated icositetrachoron).

What do you think about those proposed names? Any preference? Any other ideas? Perhaps there even might be some different construction devices? (@hedrondude: what about either of those proposed OBSAs?)

--- rk

[Klitzing]

... Hmmm, don't know whether I get completely what you bear in mind here. With respect to Stott expansions at least, the answer probably is "no". Alicias expansions seem to be exactly equivalent to the Wythoff constructions and so would not go beyond uniform ones. ...

Alicia in her 1913 article explicitely restricts to transitions from regular to semiregular polytopes and tesselations. Nowadays we would rather call those Wythoffian uniforms, i.e. anything what could be displayed by Dynkin symbols with "o" and "x" node marks only. (And we clearly now would no longer restrict to polytopes and tesselations only, we well could apply to hyperbolics alike!) Especially she restricts for that purpose to the chosen underlying symmetry, i.e. to that of the Dynkin symbol of consideration. In fact, what she described there comes out to be nothing but the transitions between any 2 Dynkin symbols, which differ just in one of their node marks.

Therefore my extended application to arbitrary subsymmetries is not only completely new, it moreover goes beyond mere uniforms. In fact, as was already shown, more general figures occur, which might include Johnson solids for cells (respectively, for dimensional independant applications: CRFs). Sure, that was my chosen intend. But its most general application to any subsymmetry even would extend CRF figures. There would well occur partial polygons and other stuff as well. And moreover that idea clearly could well be applied to non-convex cases too.

So far I have not run through all possible cases. Therefore I don't know whether there are other CRF examples out there, which would rise out of the applications of this idea. The so far mentioned ones are (so far) mere occasional examples I stumbled upon. In fact, they all are based on generalizing some few ingenuine findings of quickfur from last year. - Thus yes, thank you quickfur for unconsciously providing the seed for this quite general concept!

--- rk

[wendy]

Alicia Stott derived a notation based on expansions of a kernel. This does not call down to the Dynkin graph, and is somewhat older than any version of the Dynkin graph. The notion of 'x' and 'o' only seems that there was interest in finding all of the uniform figures, but the actual notation does suggest that expansion or contraction was 1 or 0 only. The 15 examples of 3,3,5 were thus found.

Wythoff showed that Stott expansion corresponded to half-edges to the separate mirrors of a reflective group, again for 3,3,5, showing the completeness. Robertson showed the equality of these.

Coxeter first described the Dynkin graph (it's pretty obvious from group theory: de Witt and Dynkin both found it separately relative to lie groups). When he read wythoff's paper, he had then the means to decorate the dynkin graph with wythoff-style nodes. It appears that he did understand weighted nodes, since what we call 'q' nodes appear in 'Regular Complex Polytopes'. The bulk of the rest appears in just x and o.

Using the known graphs and the Stott/Wythoff construction, he found all of what i call Wythoff Mirror-Edge figures.

Stott suggested to Coxeter a notation of an 's' node, a hollow node representing a vertex without symmetry.

My main contribution is to isolate the vertex as a separate node. In terms of vertex figures, the vertex node is connected to the balance by way of branches marked 5/2, 3, 4, 5, 6, &c. The effect of twelfty here is that a symbol like 335 might be translated to 2.95, which is not meant to happen. So there were letters, first based on the linearising of the 2_21 type symbols (4B). So these branches become v, s, q, f, h, &c.

Conway explained the magic of stott expansion in the list.

Having a separate vertex node allows for multiple vertex nodes, which in part helps Klitzing with his segmentotopes, but elsewhere describes a larger range of lacing prisms.

[Klitzing]

Wendy, I surly agree in that Alicia wrote her 1913 paper before there were Dynkin symbols to use. But now having this means, and applying that onto what is outlined in her paper, it cools down to exactly what I've said. So yes, she was ahead of those means, but her intended application can be given in that form today.

Throughout her paper she never goes beyond the application of "pulling apart" / "pushing in" to other than elements from equivalence classes with respect to full underlying symmetry, i.e. in the sense of the (undecorated) Dynkin symbol.

Applications with respect to true subsymmetries, i.e. what I called so far tentatively "partial Stott expansions / contractions", up to my knowledge never occured since. - And even if someone would have thought about that before, he/she would have thrown it apart quite soon, as that usually results in non-uniform figures, which up to this thread where clearly out of scope.

This is the point, I was stressing, when pointing out that it took exactly 100 years to extend her application that way.

--- rk

[Klitzing]

Just found more again!

we already had the following partial applications:
in 3D:

Code: Select all

x3o4o = oct <--> tut <--> x3x4o = toe

in 4D:

Code: Select all

x3o4o3o = ico  <--> thex      <--> tah       <--> x3x4o4o = tico
x3o4o3x = spic <--> owau prit <--> poc prico <--> x3x4o3x = prico


but additionally there are clearly:
in 3D:

Code: Select all

o3o4o = point <--> tet <--> o3x4o = co

in 4D:

Code: Select all

o3o4o3o = point      <--> hex <--> rit <--> o3x4o3o = rico
o3o4o3x = (dual) ico <--> A   <--> B   <--> o3x4o3x = srico


We should note (as an aside), that those 3D sequences become classical Stott sequences, when applying to the tetrahedral subsymmetry:

Code: Select all

o3y3o <--> x3y3o <--> x3y3x // where either y=o or y=x

and similarily the first of the 4D ones each can be rewritten such, when being applied to demitesseractic (= hexadecachoral) subsymmetry:

Code: Select all

o3y3o *b3o <--> x3y3o *b3o <--> x3y3x *b3o <--> x3y3x *b3x // y as above

But the second case of 4D each clearly cannot be given in closed form in that subsymmetry. Therefore those are indeed non-classical cases!

This additionally shows, that even so the other so far known application (removing resp. inserting equatorial prismatic parts in mutually orthogonal directions) applies to every dimension, this application seems to end here. In fact, we could consider to apply it likewise onto the symmetry o3o3o *b3o *b3o. But that is no longer a spherical symmetry, that one becomes a flat (euclidean) tetracomb symmetry. (Quite similar as why the Gosset figures do not exist in 9D any longer.)

Finally returning to the main topic of this mail:
The last sequence of interest would have the following cell counts respectively cell transitions:

Code: Select all

   ico*  A     B      srico
8  point point tet    co
8  point tet   tet    co
8  point tet   co     co
24 oct   esqu. squob. sirco
32 edge  edge  edge   trip
32 edge  edge  trip   trip
32 edge  trip  trip   trip


According to my mail of this morning we might call A and B respectively:

• A = poxic (partially octa-expanded ico) = phic srico (partially hexadeca-contracted srico
• B = phixic (partially hexadeca-expanded ico) = pocsric (partially octa-contracted srico

What would you think about those names (resp. OBSAs)?

--- rk

[quickfur]

... As for generalization to other symmetries, I'm not so sure, it seems difficult because n-cube symmetry is the only one with trivial dissection properties (i.e. an n-cube can be cut into smaller n-cubes evenly, which also allows trivial elongations, partial Stott expansions/contractions, etc.). One possible direction to look, though, might be the duoprisms. There, the regularity of the toroidal ridge between the two rings (consisting of a grid of squares) may make it easier to perform partial expansions, maybe? One can also look into "inflating" the rings apart so that they no longer touch each other, and filling in the gaps with CRFs (something like the grand antiprism, but not necessarily with tetrahedra -- what about square pyramids, say?). ...

One has to bear in mind that an essential ingrediant in those shown possible cases for partial Stott contractions is that no other 2D-faces other than squares are contracted, that is, the equatorial segment has to be a true prism (independent of those prismatic parts are themselves complete or in turn equatorial parts of larger cells).
[...]

I wonder if it's possible to find CRF cases for which contraction happens in a 2D way, so that it's possible to, say, shrink all n-gons that lie along a great circle to a point, or 2n-gons along a great circle shrink to n-gons? Of course, the outer surface elements will probably still need some kind of deprismation via contraction of square faces, but maybe there are more possible subsymmetries we can consider? Or are these already covered by your analysis?