Marek14 wrote:[...]
We do know how many verfs to fit around a vertex since the idea is to set an abstract polyhedron first and then try to concretize it. So when we try to fit the polygons together, we already know which structure precisely we're building.
Number of polyhedra - actually, I think that most Johnson solids' verfs are quadrangles, not triangles. Triangular verfs are surprisingly limited.
Interesting. So the dichoral angles based algo will not get very far then, if the 4D CRFs also mostly exhibit degree-4 edges.
First of all, I'm not sure how many different abstract polyhedra there is for up to 12 vertices.
Wait, why only 12? An icosahedral pyramid has 20 tetrahedra meeting at a vertex. Narrower shapes like triangular cupola may be able to fit even more around a vertex. (The 11 or 12 figure we got was for maximum number of cells around an
edge, but we're talking about
vertex figures here.)
[...] As for their convexity, that seems more complex than I thought -- what exactly does "convex" mean for a skew polyhedron that doesn't fit in a single hyperplane? Are skew polygons convex? But I guess there are two kinds of convexity that need to be checked: the local convexity of vertex which would be done while building the verfs, and the global convexity to prevent intersecting faces.
Maybe one way to check convexity would be to assemble the cells associated with the verf into an actual 4D figure (a partial polychoron - a bunch of cells around a single vertex) and check that the figure is convex. If all verfs give convex figures, then by extension the entire polychoron must be convex.
The main improvement from 4D edge to 3D vertices is that there is now only finite amount of possible distortions. Let's say that we start with an abstract polyhedron.
Step 1 -- lengths are assigned to the polyhedron's edges.
Step 2 -- check the faces to verify each matches a valid cell. If a single face does not (for example, if there's a triangle that would have a triangle, square and pentagon around), the length assignment is invalid.
Step 3 -- for each face with 4 or more edges check all possible skewings for that combination, in various orientation if necessary.
But still, you have the problem of which deformations to use to get a valid polyhedron. Just because the abstract polyhedron tells you there are 5 faces around the vertex, doesn't mean you know what dihedral angles to assign to them. So you still end up having to solve the non-rigid vertex problem. Although, I suppose you could assign verfs to faces first, so that gives you a fixed length for all the edges, then you can use that to compute the angles. Hmm. Maybe this will work after all. But how to handle the case when some verfs are non-planar?
Step 4 -- now that each face is clearly defined, the computer has to actually build them into the structure of the shape. This will involve solving a series of equations since the relationships between the vertices are described in terms of distances and angles.
Better make sure there are no systems of quadratics here!
Step 5 -- once you have the polyhedron and the paint dries a bit, you try to find a point with distance 1 from each of its vertices. If this is not possible, the polyhedron cannot serve as a verf and is discarded.
Maybe there's a way to make use of this fact to cull the number of abstract polyhedra that are generated or considered? Not sure how, though.
Step 6 -- check the convexity. Here you can also check that you didn't end up with a degenerate 2D shape, like happened with that delirious tetrahedron of mine,
Step 7 -- the verf is ready to use.
Clearly, step 4 is hardest, but it should be in capabilities of computers.
I also suspect that the more outlandish and complicated structure of the abstract polyhedron, the less chance it will actually lead to a valid verf. Most of the possibilities will be thrown out in step 5 or 6. Number of abstract polyhedra will be further culled (though probably not that much) by the fact that anything that contains hexagon or larger polygon can be discarded outright.
Hmm. I'm still not convinced that the abstract polyhedron approach will save us very much. But maybe we should put it in more concrete terms so that we can analyze it. How do we go about enumerating abstract polyhedra? You can start with n vertices, then generate all possible pairings (edges) between them, which is
(n choose 2) EDIT: no that's wrong, it should be 2^(n^2) combinations. Then from those edges, generate all possible groupings (faces) between adjacent edges, which is
(E choose k) EDIT: 2^(E^k) for E = number of edges, 3≤k≤5. That's a total of about
(n choose 2) * (E choose k) 2^(n^2 + E^k) combinations to check (loose upper bound). And you have to loop from n=4 to at least 20, maybe more. I'm not sure how to count this correctly, but it does look like a very huge number of combinations to go through.
But still, once you assign lengths to edges, how to turn that into coordinates? If all you have is a graph with labelled edges indicating length, how do you turn that into an actual polyhedron? Edge lengths constrain the location of vertices to a fixed radius from adjacent vertices, so to solve for vertex coordinates, you could fix one vertex (say at (0,0,0)), and maybe the second vertex at (x,0,0) for some x, then try to solve for the rest. Since the constraints involve radius, this gives you a system of quadratic equations.



 Wouldn't you just love to look at it from a 5Der's POV, eh? And the 24-cell 5-teddy, which may be the only CRF teddy in any dimension that contains non-simplex (n-1)-teddies for facets.
Wouldn't you just love to look at it from a 5Der's POV, eh? And the 24-cell 5-teddy, which may be the only CRF teddy in any dimension that contains non-simplex (n-1)-teddies for facets.
 I assume this is the maximum amount, but it might be a bit more.
I assume this is the maximum amount, but it might be a bit more.



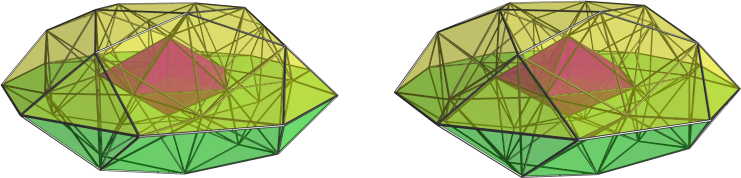
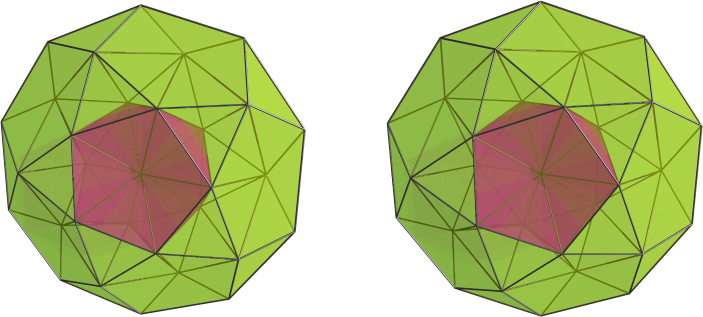
 (The missing tetrahedra are just the bits that fall out when you cut up the melon, y'know.)
(The missing tetrahedra are just the bits that fall out when you cut up the melon, y'know.)
