Keiji wrote:[...]
OK. But I don't like the word "expand" because it's ambiguous. A 5D teddy can be runcinated and still be a teddy-like shape, for example.
That's why I put the "expanded" immediately before the "teddy".
However, I accept that there's no way to distinguish between a teddy that has subsequently been expanded ("expanded (________ teddy)") and a teddy of an expanded polytope ("(expanded ________) teddy") with that nomenclature. Therefore, I now propose:
teddy =
ursatope or
ursamorphexpanded teddy =
ursa____tope or
ursa____morph where ____ is some word meaning "outside", which I also need to use for the xoo...oox uniforms.
How does that deal with cantellated, runcinated, etc., teddies? Isn't it just still equivalent to "expanded ... ursatope"?
My first thought, the obvious one, is "exo", but that doesn't go well (it creates "ursaexomorph", which gets shortened to "ursexomorph", which is rather unpleasant), although Google provides
a number of alternatives. I considered Japanese, but that is "soto", and "ursasototope" is... just a little too alliterate for my liking, although "ursasotomorph" isn't so bad.
So, if we can find a decent word here, we're all good

Well, let's run through the list of languages that I know or am somewhat familiar with:
English: ursa-out-tope > ursaouttope (sounds funny and looks weird)
Greek: ursa-ex-tope - you already discounted this one.
Latin: ditto (N.B. I don't actually know any Latin).
Russian: вы- (vy "out, out of"), внешный (vneshnyi "outside"), наружный, снаружи (naruzhnyi, snaruzhnyi): none of them looks (or sounds) particularly attractive in English.
Mandarin: wai (pronounced like "why") - not that great either: ursawaitope looks and sounds weird.
Hokkien: gua - ursaguatope. Surprisingly, this one actually doesn't look too bad.
Malay/Indonesian: luar, diluar: ursaluartope. Doesn't sound too bad, but looks a bit strange. Or "pinggir" (edge, boundary): Ursapinggirtope - looks totally bizarre.
Tagalog: labas - ursalabatope? Seems workable.
Latvian: ara: ursaaratope > ursaratope. Hmm. This might actually work! (Caveat: I don't know any Latvian. I got this from Google Translate.

)
Croatian: vanjski: maybe vanatope? Ursavanatope. Sounds nice! (except for the unfortunate substring coincidence with "savana", which might give the wrong idea).
Estonian: välis-: hmm, valitope? Ursavalitope. Not too bad.
Finnish: ulko-: ulkotope. Ursaulkotope > ursalkotope. Not too bad, just looks a bit strange.
Swedish: ute-: utetope. Ursautetope > ursutetope. Not too bad, but a bit awkward.
Romanian: periferic: maybe peritope? Peri- is also nice for "outside": perimeter. Ursaperitope. Hey I like that! Plus, "peri" is also a Greek prefix, so it's not too incongruous with the rest of the derivations (which are generally drawn from Latin/Greek). Huh, why didn't I think of this earlier.
I vote for ursaperitope! Ursavalitope would be my 2nd choice. Then maybe ursalabatope.
P.S. Romanian also has marginas-: so maybe ursamarginotope might work too. But it's a bit verbose, and maybe confusing if you start thinking of marginalized polytopes...
(OK, I lied. I don't know most of the above languages. I was just using Google Translate.

)
Certainly -- you'll get something with a hexagon on top, 3 pentagons around every other edge, with squares in between, and skirting the bottom you'll get trapeziums, and another hexagon at the bottom.
Ah yes, of course. I pretty much knew all that, but for some reason I couldn't piece it together and visualise it until you put it in your own words.

And this isn't even 4D we're talking about!
I have the opposite problem. I can visualize things quite well, but trip over the simplest calculations that's anything harder than 1+1=2. (Even that I sometimes get wrong!) I
know how to do the algebra, but I keep making silly mistakes everywhere.



 And 3-teddy for the 3D counterpart, just to avoid ambiguity. We already have
And 3-teddy for the 3D counterpart, just to avoid ambiguity. We already have  I inverted the sign of the height of the cuboctahedron, that's why the convex hull algo produced a non-CRF. You are absolutely right, the octahedral counterpart of 4-teddy exists, and is CRF.
I inverted the sign of the height of the cuboctahedron, that's why the convex hull algo produced a non-CRF. You are absolutely right, the octahedral counterpart of 4-teddy exists, and is CRF.
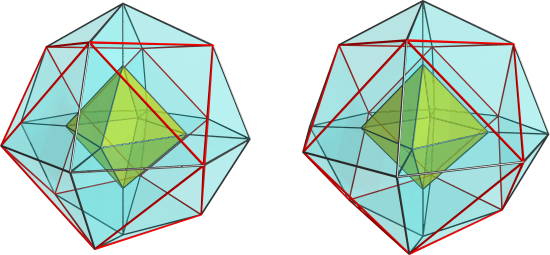
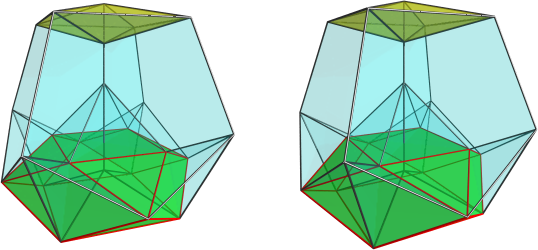
 )
)

 And this isn't even 4D we're talking about!
And this isn't even 4D we're talking about!