Klitzing wrote:[...] Esp. I got to know that in 1979 a german couple already started that 4D research in a somewhat smaller or stricter sense: they extrapolated the Johnson solid conditions in the sense of regular boundaries, i.e. of regular facets. For 4D this would mean regular cells. Those were listed all in those days, except of the various 600-cell diminishings, for sure.
So the regular-celled CRFs are already known? Is this list published or available online somewhere?
[...] The other stem for my research within the millenium change, was to provide a set of polychora which allow for an easy to grasp visualization of 4D content. So think of that research also as kind a didactical one. This is why 2 parallel vertex layers were chosen. Those figures can easily be visualized in 2 concentric settings.
True, that certainly makes it easier to introduce the subject of 4D visualization.
quickfur wrote:Have you considered the slightly larger category of monostratic Johnsons with the orbiform requirement relaxed? [...]
Well, it was kind a direct lifting of what occurs in 3D: convex segmentohedra need to have regular polygons as bases (if not degenerate). So it was easily translated into orbiform bases, as those still bow to an unique circumradius (of the base). And 2 orbiforms arranged atop of each other would allow for an unique circumradius in the next dimension up. At least the lacings would tie them accordingly so that their centers align at the axis. - Only subdimensional bases allow for a shift.
True, I guess this would keep the numbers of segmentochora manageable in higher dimensions, as well as preserve a useful common property among all of them. Relaxing the orbiform requirement would admit more and more exotic shapes as you go up into higher dimensions, since an exotic shape in one dimension opens up the opportunity for even more exotic shapes constructed from it in the next dimension.
Further these unique circumradii of the bases made it easy to calculate the height of the segmentotopes, i.e. the displacement of the hyperplanes. Additionally this guaranteed that all lacing edges would be of the same length. Thus this choice was quite helpful for the research. - Any weaker setup would get a lot harder.
True. These calculations would get very complicated quickly once the orbiform requirement is relaxed.

Still, I'm curious about what kinds of non-orbiform CRF monostratics there are, that aren't just prisms of Johnson solids. I find that the process of discovering how polyhedra can be put together to form polychora is very insightful into the workings of 4D space.
quickfur wrote:[...] On a slightly higher-level, I wonder if the enumeration of 4D Johnsons can be made somewhat more tractable if we split up the task into more directed categories where more specialized search methods can be employed. Following the way Johnson arranged the 3D Johnson solids in groups, I came up with the tentative categories:
[...]
Could give a try... But sure wont get less hard to do. And you would have the additional task to prove that this partitioning would not omit some cases...
I was thinking of using the crown jewels category as a "catch-all" category for odd shapes that don't belong to any other category. But you're right -- even if we filled out those categories, we still have to prove that we've covered everything. It seems that a computer brute-force search is the only way to conclusively prove the completeness of our list.
I rather would try to lift the prove of completeness of Normans original research directly, by means of a brute force computer research sticking allowed polyhedra face to face, with lots of freedoms of deformation until those complexes would close finally. - Just could run into problems with the sheer number of to be found polychora, so that such a program wont end within a human lifetime...

I've been thinking about that, but the major difficulty is the sheer number of 3D CRFs, which means a giant combinatorial explosion, coupled with the complexity of representing partial CRF complexes in an efficient way that would allow algorithmic detection of when something can be closed up to make a CRF polychoron.
A brute-force algorithm that Marek & I have been considering uses dihedral angles to fix dichoral angles between cells so that viable cell combinations are discovered more quickly. But it turns out that, due to non-rigid edges surrounded by more than 3 polyhedra, this algorithm will not enumerate all possibilities. So it's not suitable for proving CRF completeness, but with some tweaks, it can be used to search for CRFs up to degree-4 edges, with at least one degree-3 edge per face. It's a much smaller class of CRFs, since most of the 600-cell family CRFs would be excluded, but it may help reveal some unusual constructions that can be generalized by hand to more complex shapes.
[...] I just gave the bi-stratics some preliminary thoughts. There would be 3 classes: Stacks (i.e. towers) of monostratics with some true dihedral angles between the lacing facets; similar stacks with that angle becoming 180 degrees, so that those facets would be reconnected to towers themselves; and finally the original new ones containing true bistratic lacing facets. - Wendys xfo3oox3ooo&#xt clearly belongs to those last ones.
I think stacks/towers can be automatically enumerated by computer, since the monostratics are already known. We just compute the dichoral angles for each cell pair in the monostratics, which can also be done by computer, and that will tell us which ones can be stacked on top of each other without becoming non-convex.
The second class needs some special handling, since not all co-planar facets are Johnson. There are a finite number of allowed co-planer facets, like square pyramid + cube = elongated square pyramid, cupola + base prism = elongated cupola, etc.. Things like cube+cube would be illegal, since the convex hull would have cuboidal facets.
The last class I would regard as "true" bistratics, since they cannot be formed by cut-n-paste operations on monostratics. They're also the most interesting class.

But then I gave a thought to the diameter of the equatorial vertex layer: Esp. in the last 2 classes that one generally would not match the unique circumsphere condition. So, in view of the usefulness of unique circumradii, as stated above, we probably should restrict orbiformness to the layers only, and not ask for the total figure! But that in turn would open a can of worms for the first class: we have to determine that the dihedral angles of the lacing cells at the equatorial hyperplane still have to bow to convexity. And this asks for additional calculations here...
[...]
Hmm. While I see the usefulness of the orbiform requirement, I'm more interested in the non-orbiform cases. They would be harder to calculate, but more rewarding to discover IMO.

As for computing angles, it can probably be done by computer, since once vertex coordinates are known, a convex hull algorithm gives the face lattice, and it's easy to automate computation of dihedral/dichoral angles. This should allow us to write programs to quickly eliminate obviously non-convex combinations, then if necessary we can manually check the boundary cases (where the angle is close to 180°) where there may be inaccurate results due to roundoff error in computer arithmetic.


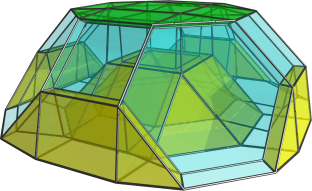
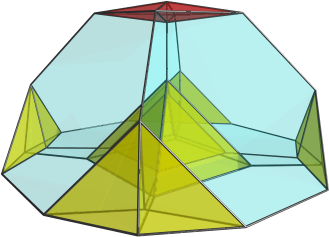


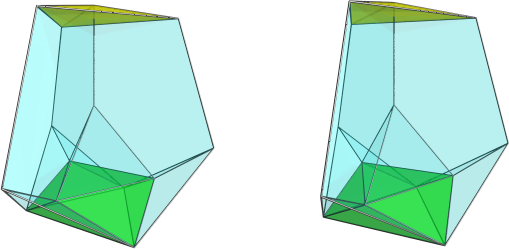




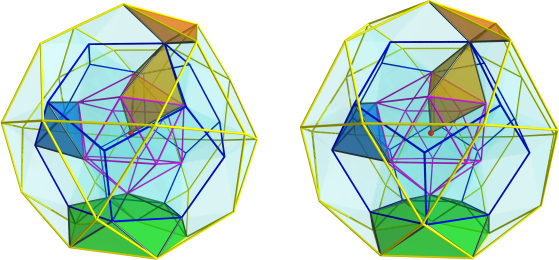
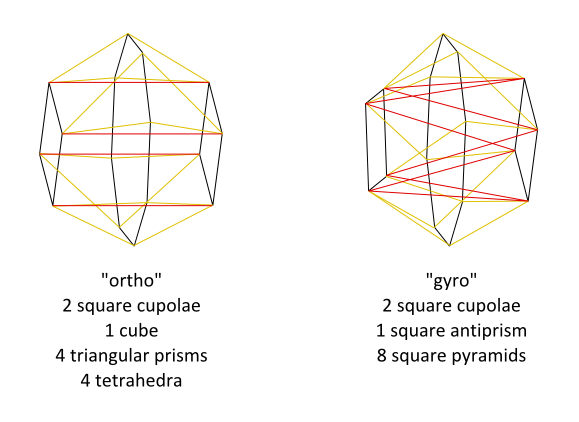

 I'm aware that my diagrams have the black square faces rotated 22.5 degrees (I think) out of line with where they should be so the square faces do not appear planar even though they are supposed to be
I'm aware that my diagrams have the black square faces rotated 22.5 degrees (I think) out of line with where they should be so the square faces do not appear planar even though they are supposed to be
 The icosidodecahedron is o3x5o, not x3o5x.
The icosidodecahedron is o3x5o, not x3o5x.