Hi, new member here.
As a favorite meditation subject of mine, I have figured out several 4-d and higher geometries. I can visualize cubes up to 5-d, and UNDERSTAND them up through 8-d (cubes are the easiest, for me). I recently managed to complete my visualization and understanding of triangles/pyramids in 4-d, and have logically progressed them through 6-d.
One shape that has eluded my grasp for a LONG time was the higher-d sphere, though. I still cannot for the life of me begin to visualize it, nor can I logically figure how to construct one. I had a recent breakthrough, when I realized (I swear, a lightbulb actually materialized over my head and blinded everyone nearby with THAT flash...) that a 2-d circle is a 1-d line curved through 2-d space to intersect all points at x distance in 2 dimensions from a given point c; a 3-d sphere is a 2-d plane curved through 3-d space to intersect all points at x distance in 3 dimensions from a given point c; thus a 4-d sphere must be a 3-d (something) curved through 4-d space to intersect all points at x distance in 4 dimensions from a given point c.
Where my new problem lies is in figuring out what the (something) is, exactly. I have a line and a plane; what is my logical procession? I am working on this exercise now. It is a tough little challenge, one I am thoroughly enjoying. Once I figure it out, I will have 3 points on my progression, and will be more easily able to extrapolate the next several.
I know that you can also view the sphere as a circle twisted a full rotation through z around the x or y bisecting axis, and a circle as a line twisted a full rotation through x around the y halfway point. But this is not the progression I am pursuing. It is not nearly as elegant. Plus it creates solid shapes, where the other model would just be the hollow skin encompassing the shape, which is far preferable for my purposes. (This was my original progression, but read on...)
In this alternate progression, the 4-d sphere would be a 3-d sphere twisted a full rotation through w around the xy, yz, or xz bisecting plane/circle. The problem is, although I can logically understand this, and probably continue the progression (5-d is 4-d twisted through v around the xyz, wxy, zwy, or wxz bisecting spheres. That would be the progression, but is it correct?) I still cannot visualize it, thus rendering myself incapable of determining of it is correct or just an example of fuzzy logic taken too far.
I wish to note, I have never looked at ANY models until I have designed my own first. I do not muddy the waters of my mind with other peoples' work; I work it out myself, then compare. It allows me to give things a fresh viewpoint, which has allowed me to come up with a few models I believe to be unique to myself. I did not have in my head already "Oh, that's what a tesseract looks like", because then any time I tried to visualize it, I'd just have seen that super-cross shape, and never been able to come up with my own versions. This methodology also allows me to more easily visualize the actual 4-d shape, rather than just the unfolded representation of each one.
Anyways, I am just excited about my progress on the hypersphere (which I have never seen a model of, yet, of course), and wished to share my thoughts.
See ya!
Some thoughts on the hypersphere.
5 posts
• Page 1 of 1
Re: Some thoughts on the hypersphere.
You may find this thread helpful
viewtopic.php?f=25&t=1641
Actually, the hyperspheres are also my most favorite higher dimensional object
My visualization techniques are also follows
1D Line
2D Spin the line about its midpoint, the figure it traces out is a circle (technically a disk)
3D Spin a circle about its diameter, the figure it traces out is a sphere (technically a ball)
4D Spin a sphere about one of its great circles (largest possible circle you can draw on the sphere, e.g. the equator), the figure trace out is a 3-sphere (technically a 4-ball)
To get from 3D to 4D
remember how a line occupies a small region of a plane and how a plane is flat relative to 3D space. In nD, (n-1)D objects occupies relatively negligible space, thus they act as if they are flat. (However, they are still fully n-1D dimensional objects). E.g. In 3D, a plane may look flat, but it is still puffy in the sense that it is a fully 2D objects. Similarly, for 3D spaces (I often like to refer them as cells or solids) they are 'flat' relative to the more spacious 4D, but they are bulky with respect to 3D space. So if you see too 3D solid bits crossing each other in the images, remember they are not actually meeting each other but are separated in the 4th direction
There are also other threads that are worth looking for, try typing "hypersphere", "glome", "3-sphere" on the search bar of this forum and see what comes out
viewtopic.php?f=25&t=1641
Actually, the hyperspheres are also my most favorite higher dimensional object
My visualization techniques are also follows
1D Line
2D Spin the line about its midpoint, the figure it traces out is a circle (technically a disk)
3D Spin a circle about its diameter, the figure it traces out is a sphere (technically a ball)
4D Spin a sphere about one of its great circles (largest possible circle you can draw on the sphere, e.g. the equator), the figure trace out is a 3-sphere (technically a 4-ball)
To get from 3D to 4D
remember how a line occupies a small region of a plane and how a plane is flat relative to 3D space. In nD, (n-1)D objects occupies relatively negligible space, thus they act as if they are flat. (However, they are still fully n-1D dimensional objects). E.g. In 3D, a plane may look flat, but it is still puffy in the sense that it is a fully 2D objects. Similarly, for 3D spaces (I often like to refer them as cells or solids) they are 'flat' relative to the more spacious 4D, but they are bulky with respect to 3D space. So if you see too 3D solid bits crossing each other in the images, remember they are not actually meeting each other but are separated in the 4th direction
There are also other threads that are worth looking for, try typing "hypersphere", "glome", "3-sphere" on the search bar of this forum and see what comes out
- Secret
- Trionian
- Posts: 162
- Joined: Tue Jul 06, 2010 12:03 pm
Re: Some thoughts on the hypersphere.
Thanks for the reply.
Your visualization technique is the same as my original technique, although you described it about a million times more elegantly than I did. This technique works wonders for logical progression, and can be used to understand any dimension I care to take it to. It just wasn't working for my visualization, is all. So I was quite excited when I came up with an alternate progression method.
Your visualization technique is the same as my original technique, although you described it about a million times more elegantly than I did. This technique works wonders for logical progression, and can be used to understand any dimension I care to take it to. It just wasn't working for my visualization, is all. So I was quite excited when I came up with an alternate progression method.
- lightandtime
- Nullonian
- Posts: 2
- Joined: Mon Apr 23, 2012 5:13 pm
Re: Some thoughts on the hypersphere.
It took me 2 years to have a better grasp on the visualization of 4D
I learnt most of the technique from other users on this forum, experience on the java applets, drawing 4D shapes diagrams, etc.
A little bit of maths do help, when it comes to check your visualization technique, though I tend not to rely on them too much, so as to make the visualization as intuitive as possible so I can teach my peers on it.
Having said that, I'm not really that good at visualization of higher dimensions. Some users such as Wendy and quickfur are good at visualizing them. You can also try this site, quickfur does really good at making this subject more intuitive
http://eusebeia.dyndns.org/4d/index
I learnt most of the technique from other users on this forum, experience on the java applets, drawing 4D shapes diagrams, etc.
A little bit of maths do help, when it comes to check your visualization technique, though I tend not to rely on them too much, so as to make the visualization as intuitive as possible so I can teach my peers on it.
Having said that, I'm not really that good at visualization of higher dimensions. Some users such as Wendy and quickfur are good at visualizing them. You can also try this site, quickfur does really good at making this subject more intuitive
http://eusebeia.dyndns.org/4d/index
- Secret
- Trionian
- Posts: 162
- Joined: Tue Jul 06, 2010 12:03 pm
Re: Some thoughts on the hypersphere.
The way I visualize n-spheres is by starting with the projection into (n-1)-dimensions, and the "inferring" nD by dimensional analogy.
For example, a 3D sphere projects into a 2D circle (well, technically, a disk -- a filled circle). Of course, a 3D sphere is certainly not "just a circle", because if you look at a picture of a sphere (which is the same as the projection of a sphere), you notice that it "bulges outward" in the center, and that half the sphere actually lies behind the circular projection image. So the shape of a 3D sphere is basically two 2D disks "sewn together" at their edges, and "inflated" so that they "bulge" into a sphere. If you drew a grid on the sphere, like this:
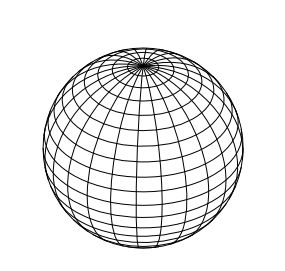
you'll notice that near the center of the image, the grid cells are closest to squares (or rectangles in this case). Near the edge of the circular image, they get increasingly distorted, because the curvature of the sphere is more pronounced there. They also appear more "squished", because they're increasingly seen from an angle.
What of a 4D sphere? It projects to a 3D sphere (or rather, a ball -- a filled sphere). But of course, it's not "just a 3D sphere", because a 4D viewer looking at a 4D sphere would see it "bulging outwards" at the center of the image, which, in this case, is the center of the 3D sphere. So a 4D sphere is basically the interiors of two 3D spheres, glued to each other at their boundaries, and "inflated" so that they bulge along the 4th axis into a 4D sphere.

So imagine if you will, the center of this sphere (where the lines converge) is "bulging outwards", not in the direction of the screen or any 3D direction, but in the 4th direction.
Near the center of the projection is where the shapes of the grid cells (which in this case are cuboidal blocks or pyramids) are least distorted; as you move outwards, they become more and more squished. This isn't very clear in the above image due to the distortions introduced by the convergence point, but it's clearer here:

The outermost layer of cells are the most "squished", signifying that that's where the curvature of the 4D sphere is most visible.
So there you have it, the 4D sphere.
Analogously, the 5D sphere can be visualized once you've mastered the 4D sphere: it basically projects to a 4D sphere where its center is "bulging outwards". This center is not the center you see in the images above (what you see in the images is just the surface of the 4D sphere), but the actual 4D center of the hypersphere. So imagine that center is "bulging outwards" in the 5th direction, and another copy of the 4D sphere bulging in the opposite direction, and there you have the 5D sphere.
You can do the same for the 6D sphere, the 7D sphere, etc..
For example, a 3D sphere projects into a 2D circle (well, technically, a disk -- a filled circle). Of course, a 3D sphere is certainly not "just a circle", because if you look at a picture of a sphere (which is the same as the projection of a sphere), you notice that it "bulges outward" in the center, and that half the sphere actually lies behind the circular projection image. So the shape of a 3D sphere is basically two 2D disks "sewn together" at their edges, and "inflated" so that they "bulge" into a sphere. If you drew a grid on the sphere, like this:

you'll notice that near the center of the image, the grid cells are closest to squares (or rectangles in this case). Near the edge of the circular image, they get increasingly distorted, because the curvature of the sphere is more pronounced there. They also appear more "squished", because they're increasingly seen from an angle.
What of a 4D sphere? It projects to a 3D sphere (or rather, a ball -- a filled sphere). But of course, it's not "just a 3D sphere", because a 4D viewer looking at a 4D sphere would see it "bulging outwards" at the center of the image, which, in this case, is the center of the 3D sphere. So a 4D sphere is basically the interiors of two 3D spheres, glued to each other at their boundaries, and "inflated" so that they bulge along the 4th axis into a 4D sphere.

So imagine if you will, the center of this sphere (where the lines converge) is "bulging outwards", not in the direction of the screen or any 3D direction, but in the 4th direction.
Near the center of the projection is where the shapes of the grid cells (which in this case are cuboidal blocks or pyramids) are least distorted; as you move outwards, they become more and more squished. This isn't very clear in the above image due to the distortions introduced by the convergence point, but it's clearer here:

The outermost layer of cells are the most "squished", signifying that that's where the curvature of the 4D sphere is most visible.
So there you have it, the 4D sphere.
Analogously, the 5D sphere can be visualized once you've mastered the 4D sphere: it basically projects to a 4D sphere where its center is "bulging outwards". This center is not the center you see in the images above (what you see in the images is just the surface of the 4D sphere), but the actual 4D center of the hypersphere. So imagine that center is "bulging outwards" in the 5th direction, and another copy of the 4D sphere bulging in the opposite direction, and there you have the 5D sphere.
You can do the same for the 6D sphere, the 7D sphere, etc..
- quickfur
- Pentonian
- Posts: 3024
- Joined: Thu Sep 02, 2004 11:20 pm
- Location: The Great White North
5 posts
• Page 1 of 1
Return to Higher Spatial Dimensions
Who is online
Users browsing this forum: No registered users and 19 guests
