And I've replaced your image links with direct links because imageshack is ridiculously full of ads. ~Keiji
A imagined story:
===============================================================================
...One day when I was eating I noticed an orange. This orange is bigger than other oranges. In fact it is more spherical than other oranges.
I grab a knife and slice it open...

===============================================================================
This is a sphere.

Looks 3D? Think again, it's in fact the 3 sphere (projection)
Rotate the sphere a bit, and the w axis is now visible

Viewing another 3 sphere edge on, results in the usual 2 sphere view plus the 3rd curvature collasped into the classical dounut shape projection (Area near the two thick vertical lines)

The 3quator and the poles of the 3 sphere.

>>>
A 3 sphere is the 4D analogue of the 2 sphere (the common 3D ball we all familiar with)
To slice the 3 sphere, apply dimension analogy:
-1 sphere (point)
A point can be sliced by emptiness into emptiness along emptiness, with emptiness as cross sections (emptiness corresponds to empty (-1) space required to make some maths complete)
0 sphere (line segment)
A line can be sliced into half along its mid point, with points as cross sections
1 sphere (circle)
A circle can be sliced into half along the diameter, with line segments of length d as cross sections
A maximum of 2 orthogonal cuts can be made to dice the circle into quarters
The quarters has the shape of a right angled triangle but with one side a curve (the surface of the circle)
2 sphere
A 2 sphere can be sliced into half along any great circles. And the cross sections are circles
A maximum of 3 orthogonal cuts can be made to dice the 2 sphere into 1/8 identical chunks
The chunks has the shape of a right angled tetrahedral shape with one curved face (the surface of the 2 sphere)
3 sphere
Similarly a 3 sphere can be sliced into half along any great 2 spheres.
Here are the various hemi 3 spheres obtained when one slice along the great 2 spheres in the x, z, y and w direction respectively

Similarly a maximum of 4 orthogonal cuts SHOULD be made to dice the 3 spheres into identical 1/16 chunks
The chunks (which the projection is not found elsewhere) are a pentachoroid composed of 4 cells of the same shape as the 1/8 chunks of the 2 sphere plus a "inflated tetrahedron" cell at the front (the surface of the 3 sphere)
Here are the 3-chunks

Another way to slice it is to
(for convenience, 2 spheres are referred as simply 'sphere' in this section)
1. Treat the 3 sphere (projection) as one sphere (squished into a spheriod in the projection) and stick it into the equator of another sphere so that the equator and one of the great circles of the "flattened" sphere intersects. (Similar to how one draw a sphere on paper, one draws a circle then mark the equator on the circle. depth thus can be inferred from the resulting image for those who can perceive 3D)
2. Choose an arbitary direction to slice, then mark 3 pairs of points anywhere on the unsquished sphere in the projection (note the points can be placed somewhere in 4D, which is done by moving the 3quator to a desired portion of of the large sphere, then mark the point anywhere on the resulting 3chord).
*3. 3 straight lines can be drawn from each pair of points and should be concurrent (intersecting at a single point). This marks the direction of the slicing plane and the poles of the spherical cross section to be obtained.
4. Connect any 4 coplanar points (lying on the same plane) to form an oval in the projection. Then choose any one pair of points directly opposite to each other on the oval and use it along with the remaining two points (which should also be directly opposite to each other) to draw another oval.
5. The two ovals (circles) should intersect at two points forming two intersecting great circles of a sphere (wireframe). Fill in the wireframe to obtain the cross sectional sphere.
6. Choose the portion of the projection to the left or right of the cross sectional sphere to discard.
7. Now the remaining portion in the projection along with the cross sectional sphere should yield the projection of the sliced chunk of the 3 sphere
(The above can be generalised to any dimensions.A n sphere requires n pairs of points forming concurrent lines to define the slicing plane. n-1 ovals can be drawn on the projection to form the n-1 great circles wireframe of the cross sectional n-1 sphere)
*It's meaingless if one cannot check whether the lines are concurrent USING THE PROJECTION ALONE and/or the above method cannot be generalized to any objects and surfaces. The slicing plane is undefined if at least one line is not concurrent
But I don't know how to develop a prove mathematically
With the 3 sphere visualized, you can easily construct the polychorons (4 polytopes) on a 3 sphere using anagolus rules in constructing their 3D conterparts on a 2 sphere.
e.g. An octahedron can be constructed by locating the 3 pairs of polear points along the 3 axes, then joint the four points on the equator to form a square and connect the 4 vetices of the equatorial square to the remaining two poles above and below the square respectively.
Similarly a 16 cell can be constructed by locating the 4 pairs of polar points on the 3 sphere. Joint the 6 points on the 3quator to form an octahedron. Then connect the 6 vertices of the 3quatorial octahedron to the remaining 2 poles ana and kata the octahedron respectively.
Here ilustrates a 16 cell drawn this way with the 3 sphere removed

These are 4 sphere and 5 sphere respectively, projected successively from its dimension to the 2D screen.


NOTE: I might be entirely wrong, cause I'm not expereinced enough to do the above mathematically nor to prove them mathematically
NOTE 2: The above ideas are result on my limited understanding of 4D plus TONS OF PAPERWORK
P.S. Imageshack doesn't allow me to upload for some reason ("no files were uploaded" error), thus i've to use facebook. IF someone manage to get into the album, mind help me rehost the pics to a more accessible place? (cause the virginbroadband does not allow me to upload them besides facebook)
P.S. 2: The facebook account above is my dummy account (old and unused anymore), thus its security and privacy is set to the lowest
P.S. 3: Due to the above problems, it took about 2 hours to get this post done



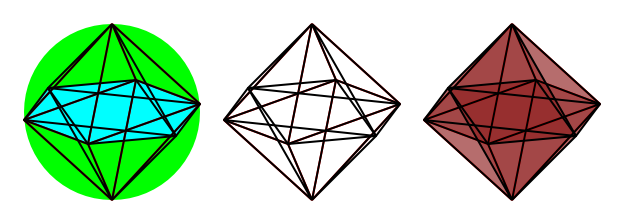
 It's fun.
It's fun.