cosine
7 posts
• Page 1 of 1
In trig functions,
co- relates to the complement (ie 90-x)
sine = height (opposite side of right angle triangle) gained for unit hypotomuse.
tan = tangent
secant = hyp/base = 1/cos
sup- relates to the supplement (ie 180-x)
versine = 1-sine (eg N-pole to lattitude) [also, suversine = sup+versine]
haversine = half of the versine.
chord = length of base of isocelese triangle, of angle x.
suchord = sup+chord.
The main trig functions i use are the chord and supchord(180/x)
co- relates to the complement (ie 90-x)
sine = height (opposite side of right angle triangle) gained for unit hypotomuse.
tan = tangent
secant = hyp/base = 1/cos
sup- relates to the supplement (ie 180-x)
versine = 1-sine (eg N-pole to lattitude) [also, suversine = sup+versine]
haversine = half of the versine.
chord = length of base of isocelese triangle, of angle x.
suchord = sup+chord.
The main trig functions i use are the chord and supchord(180/x)
The dream you dream alone is only a dream
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
the dream we dream together is reality.
\ ( \(\LaTeX\ \) \ ) [no spaces] at https://greasyfork.org/en/users/188714-wendy-krieger
-

wendy - Pentonian
- Posts: 2031
- Joined: Tue Jan 18, 2005 12:42 pm
- Location: Brisbane, Australia
When I first learned it we used the old soh, cah, toa trick. Given a triangle like the following:
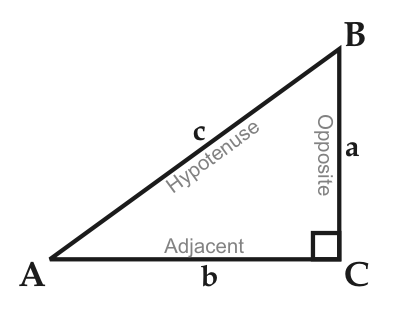
and the angle <BAC (which I will call X down below) then the you can understand the labels "opposite", "adjacent" and "hypotenuse"...the labeled opposite is just that, opposite from the angle <BAC. The one labeled adjacent is just that, right beside the angle <BAC. The one labeled hypotenuse is easy, it's the one across from the RIGHT angle, thus it's the longest line.
My soh, cah, toa rule then says that
sin(X)
= opposite / hypotenuse
(s = o/h...."soh")
cos(X)
= adjacent / hypotenuse
(c = a/h...."cah")
tan(X)
= sin(X)/cos(X)
= (opposite / hypotenuse) / (adjacent / hypotenuse)
= (opposite / adjacent)
(t = o/a...."toa")
Make sense?

and the angle <BAC (which I will call X down below) then the you can understand the labels "opposite", "adjacent" and "hypotenuse"...the labeled opposite is just that, opposite from the angle <BAC. The one labeled adjacent is just that, right beside the angle <BAC. The one labeled hypotenuse is easy, it's the one across from the RIGHT angle, thus it's the longest line.
My soh, cah, toa rule then says that
sin(X)
= opposite / hypotenuse
(s = o/h...."soh")
cos(X)
= adjacent / hypotenuse
(c = a/h...."cah")
tan(X)
= sin(X)/cos(X)
= (opposite / hypotenuse) / (adjacent / hypotenuse)
= (opposite / adjacent)
(t = o/a...."toa")
Make sense?
- houserichichi
- Tetronian
- Posts: 590
- Joined: Wed May 12, 2004 1:03 am
- Location: Canada
Re: cosine
papernuke wrote:What does the cosine mean? is it just an angle?
A more abstract answer to your question... you could think of it as a way to measure angles (though a change in sine of 0.1 isn't a constant change in angles). But, you run into problems in that you can only distinguish 180-degrees.
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
-houserichichi
cos(X)
= adjacent / hypotenuse
(c = a/h...."cah")
So that just means the the cosine of the angel X is the oppsotie end (a) divided by c?
and the same is for the sin(X) and tang(X)?
s = o/h...."soh")
- houserichichi
how can s=o/h equal "soh" isnt soh multiplication? or is that what the name/say it?
"Civilization is a race between education and catastrophe."
-H.G. Wells
-H.G. Wells
- papernuke
- Tetronian
- Posts: 612
- Joined: Sat Jul 08, 2006 6:33 pm
- Location: California, US of A
Here is another way to look at the sine and cosine functions.
Consider the unit circle (a circle with a radius of one unit centered at the origin of a Cartesian plane). Now take a line segment with one end at the origin and the other end somewhere on the unit circle. Think of it like a spinner.
This line segment forms an angle with the x-axis.It the spinner's end is to the right, then the angle is zero -- just by convention. You could pick any direction for this starting point, and it just so happens that we use that. Now if you move the spinner is a counterclockwise direction, the angle increases and keeps increasing until it come all the way around, full circle (360 degrees or 2pi radians).
If all that is clear, the rest is easy:
To obtain the value of the sine function and the cosine function for a given angle, turn the spinner to that angle. Then the y-coordinate of where the spinner lands on the circle is equal to the value of the sine, and the x-coordinate is equal the the value of the cosine.
Consider the unit circle (a circle with a radius of one unit centered at the origin of a Cartesian plane). Now take a line segment with one end at the origin and the other end somewhere on the unit circle. Think of it like a spinner.
This line segment forms an angle with the x-axis.It the spinner's end is to the right, then the angle is zero -- just by convention. You could pick any direction for this starting point, and it just so happens that we use that. Now if you move the spinner is a counterclockwise direction, the angle increases and keeps increasing until it come all the way around, full circle (360 degrees or 2pi radians).
If all that is clear, the rest is easy:
To obtain the value of the sine function and the cosine function for a given angle, turn the spinner to that angle. Then the y-coordinate of where the spinner lands on the circle is equal to the value of the sine, and the x-coordinate is equal the the value of the cosine.
- zero
- Trionian
- Posts: 139
- Joined: Wed Nov 07, 2007 5:45 am
- Location: Florida
papernuke wrote:-houserichichi
cos(X)
= adjacent / hypotenuse
(c = a/h...."cah")
So that just means the the cosine of the angel X is the oppsotie end (a) divided by c?
and the same is for the sin(X) and tang(X)?
s = o/h...."soh")
- houserichichi
how can s=o/h equal "soh" isnt soh multiplication? or is that what the name/say it?
nono...cosine is adjacent over hypotenuse. If you are trying to find the cosine of the angle that exists at the connection of the Hypotenuse line and the Adjacent line (I called that <BAC or, later, X) then
cos(X) = adj / hyp = b / c
sin(X) = opp / hyp = a / c
tan(X) = opp / adj = a / b
I was taught soh, cah, toa only to remember which three letters go together...pronounce them "so, kah, and toe-ah", they don't mean actual multiplications.
soh -> s = o / h
cah -> c = a / h
toa -> t = o / a
The one VERY important fact to remember is that hypotenuse is always across from the right angle and that the line labeled "opposite" is the one that is across from the angle you are working with. In my example I used <BAC so the line across from that is line "a". If, instead, we wanted to find cos(Y) where Y is the angle <ABC then "opposite" would be line "b" and "adjacent" would be line "a"....do you see why? Hypotenuse stays the same because the right angle didn't move.
Read the other responses too, as there's a lot more to trig than just simple number crunching like I'm making it out to be.
- houserichichi
- Tetronian
- Posts: 590
- Joined: Wed May 12, 2004 1:03 am
- Location: Canada
7 posts
• Page 1 of 1
Who is online
Users browsing this forum: No registered users and 0 guests
