Visualizations
10 posts
• Page 1 of 1
Visualizations
Understanding any geometry is apparently improved by visualizing it. Not that I am the first who has written a program to visualize geometry in various dimensions. But I've never seen the duocircle (or duocylinder or whatever you want to call the NSN-22) before. I'm very confused now.
Last edited by jensr2000 on Fri Feb 27, 2004 6:17 pm, edited 1 time in total.
- jensr2000
- Mononian
- Posts: 6
- Joined: Tue Feb 24, 2004 11:37 am
- Location: Berlin, Germany
I don't know where the NSN-22 notation comes from, but dispite what the glossary still says the duocircle is the four dimensional object:
x[sup]2[/sup] + y[sup]2[/sup] = R[sup]2[/sup]
z[sup]2[/sup] + w[sup]2[/sup] = R[sup]2[/sup]
while the duocylinder is this object lathed into the fifth dimension,
I don't know what is regularly used to denote x[sub]5[/sub] which ought to run from 0 to some length perpendicular to the duocircle above, so the duocylinder is:
x[sup]2[/sup] + y[sup]2[/sup] = R[sup]2[/sup]
z[sup]2[/sup] + w[sup]2[/sup] = R[sup]2[/sup]
x[sub]5[/sub] = 0 .. L
I've seen pictures uploaded by others then alkaline, seen no description yet how one can do that (some "sticky" posting on these perhaps alkaline(?))
Personally even pictures can tend to get somewhat foggy when the dimensions go beyond the third, perhaps you can post the formulae with the pictures.
.
x[sup]2[/sup] + y[sup]2[/sup] = R[sup]2[/sup]
z[sup]2[/sup] + w[sup]2[/sup] = R[sup]2[/sup]
while the duocylinder is this object lathed into the fifth dimension,
I don't know what is regularly used to denote x[sub]5[/sub] which ought to run from 0 to some length perpendicular to the duocircle above, so the duocylinder is:
x[sup]2[/sup] + y[sup]2[/sup] = R[sup]2[/sup]
z[sup]2[/sup] + w[sup]2[/sup] = R[sup]2[/sup]
x[sub]5[/sub] = 0 .. L
I've seen pictures uploaded by others then alkaline, seen no description yet how one can do that (some "sticky" posting on these perhaps alkaline(?))
Personally even pictures can tend to get somewhat foggy when the dimensions go beyond the third, perhaps you can post the formulae with the pictures.
.
- Aale de Winkel
- Trionian
- Posts: 182
- Joined: Wed Nov 12, 2003 2:34 pm
- Location: the Netherlands (Veghel)
Some pictures of this duocircle...
Here is a picture of several of these objects all the same size and shape but at different orientations.

Each of these are such that x<sup>2</sup> + y<sup>2</sup> = z<sup>2</sup> + w<sup>2</sup> = R<sup>2</sup>.
The top one (red) is oriented so that its x-axis goes straight into the screen, its y-axis goes to the left within each slice, its z-axis goes up, and its w-axis goes to the left across slices.
The center one (green) is oriented so that its x-axis goes straight into the screen, its y-axis goes to the left across slices, its z-axis goes up, and its w-axis goes to the left within each slice.
The final one (purple) is not axis aligned. It is rotated so that its x-axis points toward < 1, 2, 3, 5 >, its y-axis points toward < 2, -1, 0, 0 >, its z-axis points toward < 0, 0, 5, -3 >, and its w-axis points toward < 34, 68, -15, -25 >

Each of these are such that x<sup>2</sup> + y<sup>2</sup> = z<sup>2</sup> + w<sup>2</sup> = R<sup>2</sup>.
The top one (red) is oriented so that its x-axis goes straight into the screen, its y-axis goes to the left within each slice, its z-axis goes up, and its w-axis goes to the left across slices.
The center one (green) is oriented so that its x-axis goes straight into the screen, its y-axis goes to the left across slices, its z-axis goes up, and its w-axis goes to the left within each slice.
The final one (purple) is not axis aligned. It is rotated so that its x-axis points toward < 1, 2, 3, 5 >, its y-axis points toward < 2, -1, 0, 0 >, its z-axis points toward < 0, 0, 5, -3 >, and its w-axis points toward < 34, 68, -15, -25 >
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
Probably you 4d-visual insight is better then mine, I see here but some cylinder viewed from the side and from above, and some views on the crind (the 3d-intersection of two cylinder)
But it is probably my lacking visual insight, also polyhedrons polytwisters look to me like a twisted dodecahedron.
My intepretation of the formulae is that ever point on the x-y circle is a circle in the z-w plane and vice versa, this is simple to put into words, but hard to imagine dropping two dimension and putting a flatland picture to it I don't know.
But it is probably my lacking visual insight, also polyhedrons polytwisters look to me like a twisted dodecahedron.
My intepretation of the formulae is that ever point on the x-y circle is a circle in the z-w plane and vice versa, this is simple to put into words, but hard to imagine dropping two dimension and putting a flatland picture to it I don't know.
- Aale de Winkel
- Trionian
- Posts: 182
- Joined: Wed Nov 12, 2003 2:34 pm
- Location: the Netherlands (Veghel)
My intepretation of the formulae is that ever point on the x-y circle is a circle in the z-w plane and vice versa, this is simple to put into words, but hard to imagine dropping two dimension and putting a flatland picture to it I don't know.
As you go from left to right across the image above, you are seeing (two-dimensional projections of) three-dimensional slices of four-dimensional objects intersected with our three-space. The red one is being pushed through so that its w-axis is perpendicular to our three-space. The green one is being pushed through so that its y-axis is perpendicular to our three-space.
So, yes... technically, the red and green are simply sequences of cylinders (as that's what the intersection of this shape with our three-space happens to be when its w-axis is perpendicular to our three-space). The bottom one, however, is not just views of the crind. They look somewhat like it. Here's a crind:

In the picture of the duocircle above, there will be no cusp point, regardless of how one rotates it and pushes it through our three-space.
If you look across the slices of the red duocircle above, you will see that x<sup>2</sup> + y<sup>2</sup> = R<sup>2</sup> for each and every stage of the sequence where the object is pushed through our three-space. The x-axis goes into the screen, the y-axis goes to the left within each slice. If you look now at the heights of the cylinders as the item is pushed through our three-space, you will see that the height squared is the radius squared minus the squared distance from w=0.
If you look across the slices of the green duocircle above, you will see that z<sup>2</sup> + w<sup>2</sup> = R<sup>2</sup> for each and every stage of the sequence. The x-axis goes into the screen, the z-axis goes to the left within each slice, and the w-axis goes up in each slice. The y-axis is perpendicular to our three-space.
The reason we can see more slices of the red than the green is the same reason why the red cylinders on the ends are shorter than they are in diameter. Urgh.. I wish I could think of some better way to word that.
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
Something else I should have said...
My intepretation of the formulae is that ever point on the x-y circle is a circle in the z-w plane and vice versa, this is simple to put into words, but hard to imagine dropping two dimension and putting a flatland picture to it I don't know.
That's one way to think about it. The way you should think about it for the red duocircle above is that every w, the shape in (x,y,z) for that w is a cylinder whose height squared is the radius squared minus the square of the w coordinate.
The way to think about it for the green duocircle above is that for every y, the shape in (x,z,w) is a cylinder whose height squared is the radius squared minus the square of the x coordinate.
Or, more closely to what you said, if you took one of the images in the sequence of the red duocircle, that represents constant w. If, further, you sliced that piece with a horizontal cut, then you've just made a cut at a point in z-w. You end up with a circle in the x-y plane.
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
Yes, I see the red an green cylinder projections, (the red and green pictures).
The purple is a bit foggy, but probably the best one can do of the more general projection. If time permits I'll try to figure out by formulae what these are supposed to show, the red and green are very obvious z simply runs from -sqrt(R[sup]2[/sup] - w[sup]2[/sup]) to sqrt(R[sup]2[/sup] - w[sup]2[/sup]). The purple pictures form a quite curious set.
As said, I've poor 4d-visual insight
.
btw, in the other thread alkaline already mentioned the crind is officially called the Steinmetz Solid:
http://mathworld.wolfram.com/SteinmetzSolid.html
for details and picture
.
The purple is a bit foggy, but probably the best one can do of the more general projection. If time permits I'll try to figure out by formulae what these are supposed to show, the red and green are very obvious z simply runs from -sqrt(R[sup]2[/sup] - w[sup]2[/sup]) to sqrt(R[sup]2[/sup] - w[sup]2[/sup]). The purple pictures form a quite curious set.
As said, I've poor 4d-visual insight
.
btw, in the other thread alkaline already mentioned the crind is officially called the Steinmetz Solid:
http://mathworld.wolfram.com/SteinmetzSolid.html
for details and picture
.
- Aale de Winkel
- Trionian
- Posts: 182
- Joined: Wed Nov 12, 2003 2:34 pm
- Location: the Netherlands (Veghel)
Note that my homepage is still under construction, but here are the images and the program I was talking about.
http://www.geocities.com/jensruegenhagen
http://www.geocities.com/jensruegenhagen
- jensr2000
- Mononian
- Posts: 6
- Joined: Tue Feb 24, 2004 11:37 am
- Location: Berlin, Germany
Here's an animated version of the duo-circles that I pictured above rotating around a bunch.
Rotating duo-circles
I mentioned above that there wouldn't be anything like the cusp in the crind. I spoke way too soon. I was thinking only about the area in the center. It turns out, there are quite a few cusp points. But, they are like the cusp points at the "corners" of the crind above rather than like the ones in the center.
Rotating duo-circles
I mentioned above that there wouldn't be anything like the cusp in the crind. I spoke way too soon. I was thinking only about the area in the center. It turns out, there are quite a few cusp points. But, they are like the cusp points at the "corners" of the crind above rather than like the ones in the center.
Last edited by pat on Thu Mar 04, 2004 4:07 pm, edited 1 time in total.
- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
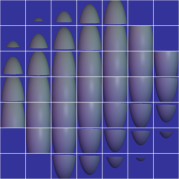
Here's some more cylinders...
Following are B<sup>2</sup> extruded into 5-d, B<sup>3</sup> extruded into 5-d, B<sup>4</sup> extruded into 5-d, and B<sup>5</sup>. All of them are in the same orientation and colored based on the normal vector at that point.







- pat
- Tetronian
- Posts: 563
- Joined: Tue Dec 02, 2003 5:30 pm
- Location: Minneapolis, MN
10 posts
• Page 1 of 1
Who is online
Users browsing this forum: No registered users and 36 guests
