Hi.gher. Space

by **quickfur** » Fri Jan 29, 2016 12:17 am

Today I started exploring diminishings of the 600-cell that feature dodecahedral cells. I started by cutting off two layers of cells to make a dodecahedral cell, then made two more similar cuts to obtain a linear chain of 3 dodecahedra along a great circle. Turns out that the dichoral angles between the dodecahedra is small enough that another dodecahedron would not fit along the same great circle; but the first and last dodecahedra can be connected to close the great circle by a pentagonal antiprism.

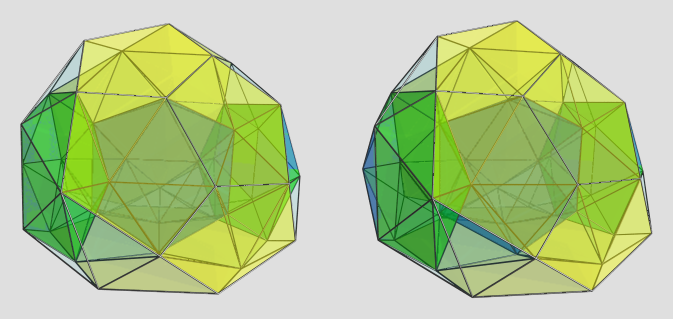
This sets the basic structure of this CRF. After that, I looked around the result a bit to see what else can be diminished to yield a more-or-less symmetrical structure. Around the pentagonal antiprism, it looked like deleting a circle of 10 vertices would produce a ring of teddies (tridiminished icosahedra) around it in alternating orientation. Furthermore, another 10 vertices can be deleted above 10 of the faces of the middle dodecahedron (where they are not shared with the adjacent dodecahedra), yielding two adjacent rings of icosahedral wedges (metabidiminished icosahedra) that encircle the two pentagonal faces shared between the middle dodecahedron and the two adjacent dodecahedra. The remaining gaps are filled by an alternating ring of 10 tetrahedra connected by their vertices. Each tetrahedron shares an edge with a great circle of edges that lies orthogonal to the plane of the 3-dodecahedron + antiprism ring.

The overall shape is a kind of blunt wedge, or trapezoidal shape with pentagonal symmetry. Here are some projections of it:

Side-view, showing the blunt-wedge shape:

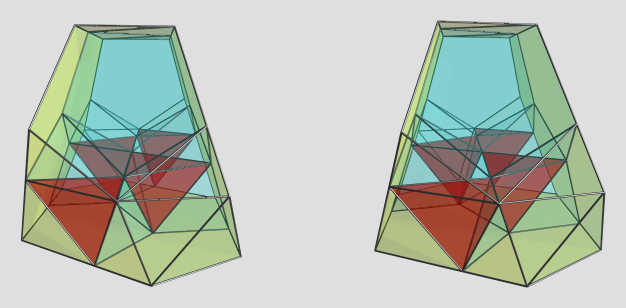
The "blunt edge" of the shape (projected to the top here) is the pentagonal antiprism; the other 3 sides are the 3 dodecahedra. The metabidiminished icosahedra lie between the red tetrahedra. There are actually 6 tetrahedra visible in this projection, but for clarity I didn't color the two that lie on the limb of the projection (they are at 90° to the 4D viewpoint). The far side of the polytope has the same structure but in skewed orientation, making a total of 10 tetrahedra.

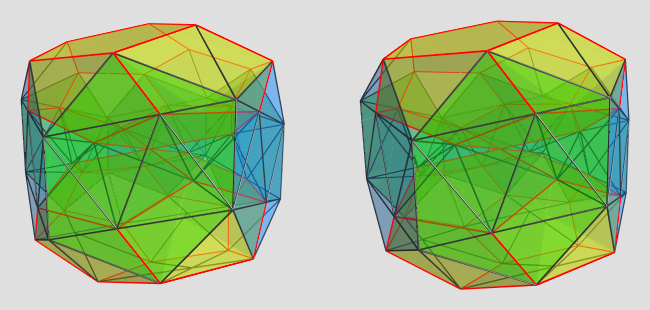
Projection centered on middle dodecahedron:

The big yellow dodecahedron is the one in the center. You can see parts of the other two dodecahedra as yellow pentagons on the top and bottom. The metabidiminished icosahedra are clearly seen, and the edges around outer faces of the tetrahedra trace out the bottom of the teddies that lie on the far side of the polytope from this viewpoint.

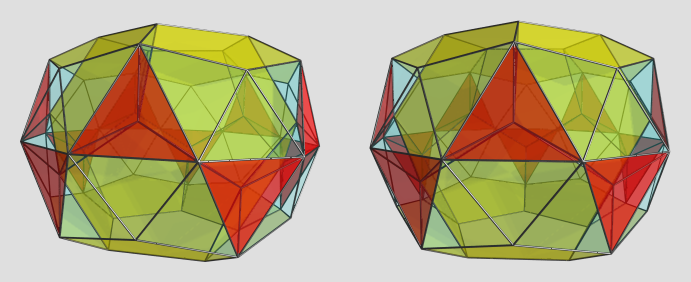
Projection centered on pentagonal antiprism:

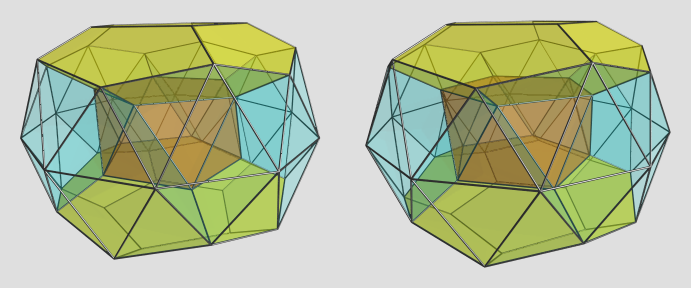
Here we see the pentagonal antiprism sandwiched between the other two dodecahedra. If you look carefully, you can see teddies attached to each of the triangular faces of the antiprism, with their bottoms pointing outwards.

This polytope has 60 vertices, 170 edges, 144 faces (100 triangles, 44 pentagons), and 34 cells (10 tetrahedra, 10 metabidiminished icosahedra, 10 tridiminished icosahedra, 3 dodecahedra, and 1 pentagonal antiprism).

Here are the coordinates of the 60 vertices (scaled such that the edge length is 2):

Code: Select all: # phi = (1+sqrt(5))/2 = golden ratio <0, 0, ±2*phi, 0> <0, ±2*phi, 0, 0> <0, ±1, ±phi, -phi^2> <0, ±phi, ±phi^2, -1> <0, ±phi^2, ±1, phi> <±1, 0, ±phi^2, phi> <±1, ±phi, 0, -phi^2> <±1, ±phi^2, ±phi, 0> <-phi, 0, 1, -phi^2> <phi, 0, -1, -phi^2> <-phi, ±1, phi^2, 0> <phi, ±1, -phi^2, 0> <±phi, ±phi^2, 0, -1> <-phi^2, 0, phi, -1> <phi^2, 0, -phi, -1> <±phi^2, ±1, 0, phi> <-phi^2, ±phi, 1, 0> <phi^2, ±phi, -1, 0> <±phi, ±phi, ±phi, phi>

by **Klitzing** » Fri Jan 29, 2016 4:07 pm

Ah, I understand what you are after here.

Just consider the lace city display of ex (600-cell) wrt. o5o2o5o subsymmetry. There you'll have:

Code: Select all: o5o o5o o5x x5o x5o o5o o5o f5o o5f o5f o5x o5x f5o f5o o5o x5x o5o o5f o5f x5o x5o f5o f5o o5f o5o o5o o5x o5x x5o o5o o5o

Then you cut off 3 times a 2-segmental cap, each uderneath an ex vertex, providing as sefa (sectioning facet underneath) these does (dodecahedra):

Code: Select all: x5o f5o o5f o5f o5x f5o f5o o5o x5x o5f o5f x5o f5o f5o o5f o5x

Finally you cut off the remaining single vertex from that former "outer circuit" (great circle) of 10 vertices, this time just a single segment of depth. - Without the former diminishings this then would result in a cut off of an ikepy (icosahedral pyramid) only. But now you just cut off a pappy (pyramid above a 5-antiprism). - Thus your final lace city here becomes:

Code: Select all: x5o f5o o5f o5f o5x f5o f5o x5x o5f o5f x5o f5o f5o o5f o5x

This projection then additionally provides that this multi-wedge has dihedral angles of 72° at the pentagons between the does and that it has dihedral angles of 108° at the pentagons between doe and pap (5-antiprism).

Nice find of yours, indeed!

--- rk

by **quickfur** » Fri Jan 29, 2016 4:22 pm

I also considered a different way of proceeding after the initial cuts that produce the 3 dodecahedra and antiprism. Instead of trimming the vertices around these cells to make diminished icosahedra, one could instead delete the great circle of 10 vertices that lie orthogonal to the plane of these cells, thereby creating a ring of 10 pentagonal antiprisms. In that case, we find that we obtain a diminishing of the grand antiprism containing 3 dodecahedra!

by **Klitzing** » Fri Jan 29, 2016 4:48 pm

Oops, it just occured to me, that you used (in that first mentioned one with pics) also several mibdis (metabidim. ikes) and teddis (tridim. ikes). That is, my just posted lace city is still wrong. As that one still contains their circumcenters as additional vertices. When those additionally are to be erased, then we are left with

Code: Select all: x5o f5o o5f o5x f5o x5x o5f x5o f5o o5f o5x

which then provides truely your vertex count (60).

So your CRF is a bit different from the mere multi-wedge, I'd just described (having 80 vertices instead).

--- rk

by **quickfur** » Fri Jan 29, 2016 11:05 pm

I found another interesting diminishing of the 600-cell today, along similar lines, sporting dodecahedral cells. This time, it's a more symmetrical one: it has 3 dodecahedra in a ring, sharing vertices, and 6 icosahedra in an orthogonal ring, sharing faces. Thus, it has a kind of 3,6-duoprism symmetry.

The construction again starts by diminishing two layers of vertices from the 600-cell to produce a dodecahedron. Next, instead of finding another cut that produces a dodecahedron sharing faces with the first one, we find a cut that produces a dodecahedron that only touches the first one at a vertex. This is uniquely determined, since at any other angle the second dodecahedron will share at least an edge. The angle between the two dodecahedra turns out to be exactly 60°, so a third cut is possible, with the third dodecahedron touching the first two at two of its antipodal vertices. This gives us the trigonal symmetry.

Each pentagonal face of the dodecahedra connect with pentagonal pyramids, with adjacent pentagonal pyramids interlocking in interesting ways.

Next, looking at the remaining surface of the 600-cell between these dodecahedra, we find that there's enough space squeeze in icosahedra along an orthogonal ring, sharing edges with the dodecahedra. It turns out that it's possible to delete 6 more vertices along this ring, producing 6 icosahedra sharing faces with each other. This gives us the hexagonal symmetry.

So this CRF has a nice 3,6-duoprism symmetry, and seems to be somewhat related to the snub 24-cell, which also has 6-membered rings of icosahedra sharing faces. It isn't a true diminishing of the snub 24-cell, because some of the dodecahedra's vertices do not lie on an inscribed snub 24-cell. Nevertheless, it does share a similar structure of one of the rings of 6 icosahedra.

Anyway, here are some pictures:

This is an orthogonal projection looking straight at one of the icosahedral cells. You can see how the 3 dodecahedra, in yellow, wrap tightly around the ring of icosahedra. Interfacing these two rings are pentagonal pyramids and tetrahedra. The tetrahedra form quite an intricate structure; there are 90 tetrahedra in total, with 30 tetrahedra in a ring system between each pair of dodecahedra. Tetrahedra from different rings are disconnected, except for a few that touch at their vertices. Within each ring, not all 30 tetrahedra are equivalent; there are at least two classes: those that share faces with two adjacent icosahedra, and those that snake around the pentagonal pyramids. I made a graph of their face connectivity, and it showed up as a 24-membered ring with 6 branches to isolated nodes (probably the tetrahedra that sit between two icosahedra).

Here's another projection, looking at one of the dodecahedral cells:

Due to the large number of visually-conflicting edges, I colored the edges of the dodecahedron red to make them easier to discern. You can see how the ring of icosahedra wrap around the 3-fold symmetry of the dodecahedron, sharing edges of alternating orientation.

Here's a look at the joint between two dodecahedra:

You can see how 3 pentagonal pyramids attached to one dodecahedron straddle 3 pentagonal pyramids attached to the second dodecahedron in an interesting alternating fashion, with a band of tetrahedra wrapping around them and interfacing with the outer ring of icosahedra.

In total, there are 75 vertices, 306 edges, 366 faces (330 triangles, 36 pentagons), and 135 cells (90 tetrahedra, 36 pentagonal pyramids, 6 icosahedra, and 3 dodecahedra).

Here are the coordinates:

Code: Select all: <0, 0, 0, -(1+sqrt(5))> <0, 0, ±1+sqrt(5), 0> <0, ±1+sqrt(5), 0, 0> <±1+sqrt(5), 0, 0, 0> <0, -1, (1+sqrt(5))/2, -(3+sqrt(5))/2> <0, 1, -(1+sqrt(5))/2, -(3+sqrt(5))/2> <0, -(1+sqrt(5))/2, ±(3+sqrt(5))/2, 1> <0, -(1+sqrt(5))/2, (3+sqrt(5))/2, -1> <0, (1+sqrt(5))/2, -(3+sqrt(5))/2, ±1> <0, (1+sqrt(5))/2, (3+sqrt(5))/2, 1> <0, -(3+sqrt(5))/2, ±1, (1+sqrt(5))/2> <0, -(3+sqrt(5))/2, 1, -(1+sqrt(5))/2> <0, (3+sqrt(5))/2, -1, ±(1+sqrt(5))/2> <0, (3+sqrt(5))/2, 1, (1+sqrt(5))/2> <-1, 0, ±(3+sqrt(5))/2, (1+sqrt(5))/2> <-1, 0, (3+sqrt(5))/2, -(1+sqrt(5))/2> <1, 0, -(3+sqrt(5))/2, ±(1+sqrt(5))/2> <1, 0, (3+sqrt(5))/2, (1+sqrt(5))/2> <-1, (1+sqrt(5))/2, 0, -(3+sqrt(5))/2> <1, -(1+sqrt(5))/2, 0, -(3+sqrt(5))/2> <-1, ±(3+sqrt(5))/2, (1+sqrt(5))/2, 0> <1, ±(3+sqrt(5))/2, -(1+sqrt(5))/2, 0> <-(1+sqrt(5))/2, 0, 1, -(3+sqrt(5))/2> <(1+sqrt(5))/2, 0, -1, -(3+sqrt(5))/2> <-(1+sqrt(5))/2, 1, ±(3+sqrt(5))/2, 0> <(1+sqrt(5))/2, -1, ±(3+sqrt(5))/2, 0> <-(1+sqrt(5))/2, ±(3+sqrt(5))/2, 0, 1> <-(1+sqrt(5))/2, (3+sqrt(5))/2, 0, -1> <(1+sqrt(5))/2, -(3+sqrt(5))/2, 0, ±1> <(1+sqrt(5))/2, (3+sqrt(5))/2, 0, 1> <-(3+sqrt(5))/2, 0, ±(1+sqrt(5))/2, 1> <-(3+sqrt(5))/2, 0, (1+sqrt(5))/2, -1> <(3+sqrt(5))/2, 0, -(1+sqrt(5))/2, ±1> <(3+sqrt(5))/2, 0, (1+sqrt(5))/2, 1> <-(3+sqrt(5))/2, ±1, 0, (1+sqrt(5))/2> <-(3+sqrt(5))/2, 1, 0, -(1+sqrt(5))/2> <(3+sqrt(5))/2, -1, 0, ±(1+sqrt(5))/2> <(3+sqrt(5))/2, 1, 0, (1+sqrt(5))/2> <±(3+sqrt(5))/2, -(1+sqrt(5))/2, 1, 0> <±(3+sqrt(5))/2, (1+sqrt(5))/2, -1, 0> <-(1+sqrt(5))/2, -(1+sqrt(5))/2, ±(1+sqrt(5))/2, (1+sqrt(5))/2> <(1+sqrt(5))/2, -(1+sqrt(5))/2, ±(1+sqrt(5))/2, ±(1+sqrt(5))/2>

by **Klitzing** » Sat Jan 30, 2016 11:44 am

And here follows now the incidence matix of that first fellow.
I'll use the following vertex type descriptions (provided at the right end of the matrix) as are shown now in this recap of its lace city:

Code: Select all: x5o A f5o o5f C E o5x F f5o B x5x D o5f x5o f5o o5f o5x | | | +- doe | | +------------- non-CRF para-bidim. id | +-------------------- f-pap +-------------------------------- pap

then it runs as follows:

Code: Select all: 10 * * * * * | 2 1 1 0 0 0 0 0 0 0 0 0 0 | 1 2 2 1 0 0 0 0 0 0 0 0 0 0 | 1 1 2 0 0 0 A * 10 * * * * | 0 1 0 2 1 2 0 0 0 0 0 0 0 | 0 3 0 1 2 2 1 0 0 0 0 0 0 0 | 1 0 3 1 0 0 B * * 10 * * * | 0 0 1 0 1 0 2 2 0 0 0 0 0 | 0 0 2 1 0 2 0 1 2 1 0 0 0 0 | 0 1 2 1 1 0 C * * * 10 * * | 0 0 0 0 0 2 2 0 2 2 0 0 0 | 0 0 0 0 1 2 2 2 2 0 2 1 0 0 | 0 0 2 2 2 0 D * * * * 10 * | 0 0 0 0 0 0 0 2 0 2 1 0 0 | 0 0 1 0 0 0 0 0 2 2 1 2 0 0 | 0 1 1 0 3 0 E * * * * * 10 | 0 0 0 0 0 0 0 0 0 0 1 2 2 | 0 0 0 0 0 0 0 0 0 2 0 2 1 3 | 0 1 0 0 3 1 F ------------------+----------------------------------------+-----------------------------------------+--------------- 2 0 0 0 0 0 | 10 * * * * * * * * * * * * | 1 1 1 0 0 0 0 0 0 0 0 0 0 0 | 1 1 1 0 0 0 1 1 0 0 0 0 | * 10 * * * * * * * * * * * | 0 2 0 1 0 0 0 0 0 0 0 0 0 0 | 1 0 2 0 0 0 1 0 1 0 0 0 | * * 10 * * * * * * * * * * | 0 0 2 1 0 0 0 0 0 0 0 0 0 0 | 0 1 2 0 0 0 0 2 0 0 0 0 | * * * 10 * * * * * * * * * | 0 2 0 0 1 0 0 0 0 0 0 0 0 0 | 1 0 2 0 0 0 0 1 1 0 0 0 | * * * * 10 * * * * * * * * | 0 0 0 1 0 2 0 0 0 0 0 0 0 0 | 0 0 2 1 0 0 0 1 0 1 0 0 | * * * * * 20 * * * * * * * | 0 0 0 0 1 1 1 0 0 0 0 0 0 0 | 0 0 2 1 0 0 0 0 1 1 0 0 | * * * * * * 20 * * * * * * | 0 0 0 0 0 1 0 1 1 0 0 0 0 0 | 0 0 1 1 1 0 0 0 1 0 1 0 | * * * * * * * 20 * * * * * | 0 0 1 0 0 0 0 0 1 1 0 0 0 0 | 0 1 1 0 1 0 0 0 0 2 0 0 | * * * * * * * * 10 * * * * | 0 0 0 0 0 0 1 1 0 0 1 0 0 0 | 0 0 1 1 1 0 0 0 0 1 1 0 | * * * * * * * * * 20 * * * | 0 0 0 0 0 0 0 0 1 0 1 1 0 0 | 0 0 1 0 2 0 0 0 0 0 1 1 | * * * * * * * * * * 10 * * | 0 0 0 0 0 0 0 0 0 2 0 2 0 0 | 0 1 0 0 3 0 0 0 0 0 0 2 | * * * * * * * * * * * 10 * | 0 0 0 0 0 0 0 0 0 1 0 0 1 1 | 0 1 0 0 1 1 pap-base-edges 0 0 0 0 0 2 | * * * * * * * * * * * * 10 | 0 0 0 0 0 0 0 0 0 0 0 1 0 2 | 0 0 0 0 2 1 pap-lacings ------------------+----------------------------------------+-----------------------------------------+--------------- 5 0 0 0 0 0 | 5 0 0 0 0 0 0 0 0 0 0 0 0 | 2 * * * * * * * * * * * * * | 1 1 0 0 0 0 2 3 0 0 0 0 | 1 2 0 2 0 0 0 0 0 0 0 0 0 | * 10 * * * * * * * * * * * * | 1 0 1 0 0 0 2 0 2 0 1 0 | 1 0 2 0 0 0 0 2 0 0 0 0 0 | * * 10 * * * * * * * * * * * | 0 1 1 0 0 0 1 1 1 0 0 0 | 0 1 1 0 1 0 0 0 0 0 0 0 0 | * * * 10 * * * * * * * * * * | 0 0 2 0 0 0 0 2 0 1 0 0 | 0 0 0 1 0 2 0 0 0 0 0 0 0 | * * * * 10 * * * * * * * * * | 0 0 2 0 0 0 0 1 1 1 0 0 | 0 0 0 0 1 1 1 0 0 0 0 0 0 | * * * * * 20 * * * * * * * * | 0 0 1 1 0 0 0 1 0 2 0 0 | 0 0 0 0 0 2 0 0 1 0 0 0 0 | * * * * * * 10 * * * * * * * | 0 0 1 1 0 0 0 0 1 2 0 0 | 0 0 0 0 0 0 2 0 1 0 0 0 0 | * * * * * * * 10 * * * * * * | 0 0 0 1 1 0 0 0 1 1 1 0 | 0 0 0 0 0 0 1 1 0 1 0 0 0 | * * * * * * * * 20 * * * * * | 0 0 1 0 1 0 0 0 1 0 2 2 | 0 0 0 0 0 0 0 2 0 0 2 1 0 | * * * * * * * * * 10 * * * * | 0 1 0 0 1 0 0 0 0 2 1 0 | 0 0 0 0 0 0 0 0 1 2 0 0 0 | * * * * * * * * * * 10 * * * | 0 0 1 0 1 0 0 0 0 1 2 2 | 0 0 0 0 0 0 0 0 0 2 2 0 1 | * * * * * * * * * * * 10 * * | 0 0 0 0 2 0 0 0 0 0 0 5 | 0 0 0 0 0 0 0 0 0 0 0 5 0 | * * * * * * * * * * * * 2 * | 0 1 0 0 0 1 0 0 0 0 0 3 | 0 0 0 0 0 0 0 0 0 0 0 1 2 | * * * * * * * * * * * * * 10 | 0 0 0 0 1 1 ------------------+----------------------------------------+-----------------------------------------+--------------- 10 10 0 0 0 0 | 10 10 0 10 0 0 0 0 0 0 0 0 0 | 2 10 0 0 0 0 0 0 0 0 0 0 0 0 | 1 * * * * * doe 5 0 5 0 5 5 | 5 0 5 0 0 0 0 10 0 0 5 5 0 | 1 0 5 0 0 0 0 0 0 5 0 0 1 0 | * 2 * * * * doe 2 3 2 2 1 0 | 1 2 2 2 2 4 2 2 1 2 0 0 0 | 0 1 1 2 2 2 1 0 2 0 1 0 0 0 | * * 10 * * * mibdi 0 1 1 2 0 0 | 0 0 0 0 1 2 2 0 1 0 0 0 0 | 0 0 0 0 0 2 1 1 0 0 0 0 0 0 | * * * 10 * * tet 0 0 1 2 3 3 | 0 0 0 0 0 0 2 2 1 4 3 1 2 | 0 0 0 0 0 0 0 1 2 1 1 2 0 1 | * * * * 10 * teddi 0 0 0 0 0 10 | 0 0 0 0 0 0 0 0 0 0 0 10 10 | 0 0 0 0 0 0 0 0 0 0 0 0 2 10 | * * * * * 1 pap

--- rk

by **Klitzing** » Sat Jan 30, 2016 1:32 pm

quickfur wrote:I found another interesting diminishing of the 600-cell today, along similar lines, sporting dodecahedral cells. This time, it's a more symmetrical one: it has 3 dodecahedra in a ring, sharing vertices, and 6 icosahedra in an orthogonal ring, sharing faces. Thus, it has a kind of 3,6-duoprism symmetry.

...

...

And here is the according lace city. The 3 dodecahedra are spotted immediately as the sides of the trigon. Moreover it is evident that those connect at vertices only. The central vertices (of the former ex) in this projection likewise are rejected. These were the tips of the 6 icosahedral pyramids.

Code: Select all: o3o o3f f3o f3x x3f o3F F3o x3f F3o o3F f3x f3o o3F F3o o3f o3o o3f f3x x3f f3o o3o

(as usual: |x| = 1, |f| = 1.618, |F| = |f|² = 2.618)

--- rk

by **Klitzing** » Tue Aug 16, 2016 2:46 pm

After being rather quiet in this forum these days, I tried to bring up a further interesting CRF to wake you up again.

To that reason I started with a dodecahedron (doe). So we have pentagons to adjoin. Here a good idea would be to use either gyroelongated pentagonal pyramids (gyepip, J11), metabidiminished icosahedra (mibdi, J62), or tridiminished ones (teddi, J63). The first ones would be not much interesting, as we would end in a way too simple hexacosachoron (ex) diminishing.

Therefore I tried the other ones. Those, when applied, then would break the symmetries of the pentagons. This is possible to be done systematically, when using the pyritohedral subsymmetry of doe.

When trying teddies this fails, because the omitted icosahedral (ike) vertices of one teddi would then still be required from the neighbouring one. But when using mibdies instead, we will get V-shaped gaps of pentagons at the 6 mutually orthogonal special edges. There then can be inserted one more mibdi each. That one then settles the overall curvature too. Thus we get back again to an ex diminishing. But that one looks not too familliar, as it uses pyritohedral symmetry in axial direction!

Therefore, the remainder surely can be filled with tetrahedra (tet) only. But on the other hand, the second set of mibdies just reaches as far as the opposite doe facet of ex. So we could fill the remainder with correspondingly fewer tets and 12 pentagonal pyramids (peppy) instead.

While thus having described that fellow already constructively, I furthermore wanted to understand that one by means of vertex layers. To that end we know already that ex can be described as point || ike || doe || f-ike || id || f-ike || doe || ike || point.
Thus we will have to chop off both outer layers down to the doe facet, that is use deep diminishings there. Next we want to place mibdies. Mibdies are in turn diminished ikes and thus further shallow diminishings of ex. Thus each such mibdi deletes one further vertex of ex directly above eauch pentagon of one of those does. In sum this deletes the full next layer (f-ike). Thereafter we aimed to place a further set of 6 mibdies atop those special edges of doe. This then deletes again one vertex each in the next layer above, that is, we delete an octahedral subset of those id vertices.

When applying this to the lace city of ex (here for sure that one in o2o2o2o symmetry)

Code: Select all: o2o -- point o2x f2o x2f f2o o2x -- ike x2o f2f o2F F2x o2F f2f x2o -- doe o2f F2o f2F F2o o2f -- f-ike o2o f2x x2F F2f Vo2oV F2f x2F f2x o2o -- id o2f F2o f2F F2o o2f -- f-ike x2o f2f o2F F2x o2F f2f x2o -- doe o2x f2o x2f f2o o2x -- ike o2o -- point

we would come out with the following lace city of the here described 2+12+6-diminishing of ex:

Code: Select all: x2o f2f o2F F2x o2F f2f x2o -- doe f2x x2F F2f F2f x2F f2x -- id \ fq-oct o2f F2o f2F F2o o2f -- f-ike x2o f2f o2F F2x o2F f2f x2o -- doe

Last but not least that resulting rectangular shape of the lace city, featuring one mibdi each on either side (as vertical column), is quite pleasing. Ain't it?

--- rk

by **Klitzing** » Thu Aug 18, 2016 5:21 pm

Thought about replacing the "doe + 3 mibdi around an edge" theme of the above figure by some "x3xPo + 3 tut", i.e. of replacing base / lacing pentagons by hexagons.

The relevant starting sequence of such a tower then is xuxo...-3-xoop...-P-oxux...-&#xt, where p = x(P,2) = 2 cos(pi/P).

For P=2 we then can finish right at that level, because of p=o here.
Sadly the outcome is already a known uniform, it just happens to be tip = x3x3o3o.
For P=3 we also can finish right there as well, because of p=x then.
Sadly that outcome also is known already to be uniform, as it then results in thex = x3x3o4o.
The case P=4 leads to a contradiction to CRF, because p=q here, and we don't have some xo..3oq..&#xt 3D-CRF.
The final case P=5 then has to be expanded way beyond that level.
My current estimate is a still un-closed tower xuxoooxf...-3-xoofxuxu...-5-oxuxuxfo...-&#xt,
which, if I got it right, so far incorporates 20+30+20 tut + 12 pap + 1+12 ti + 20 teddi + ...

Would anyone like to take the chance and try to close that P=5 fellow?
At least, when it could be closed somehow, it would be a true CRF, right because of those already contained teddies!

--- rk

by **Klitzing** » Thu Aug 18, 2016 5:34 pm

Forgot to mention first, that the recently described axially pyrohedral ex diminishing amounts in a total of 132 cells:
2 does + 18 mibdies (J62) + 12 peppies (J2) + 100 tets.

--- rk

by **Klitzing** » Tue Feb 14, 2017 10:57 pm

Half a year after the last post in this thread! And indeed quite silent within this forum in general in the last time. $:\$
So I thought it would be good to be revived.

Thought about placing triples of mibdies (J62's) onto neighbouring of pentagons of an id (icosidodecahedron). And atop the central triangle a teddi (J63). Continue with that with the remainder of id (which works) and then fill up this partial complex with tets (tetrahedra) up to the level of the tops of the teddies. There then a final ike (icosahedron) could be placed to close that CRF.

Even so this CRF just happens to be a special heptadeca-diminishing of the rotunda (hemiglome) of ex (hexacosachoron), it is kind of interesting as it implements a directed axially tetrahedral subsymmetry of the former directed axially icosahedral symmetry of that rotunda. And as such it then happens to be a chiral one as well. This chirality also can be seen from its following lace city display:

Code: Select all: x3o o3f f3o o3x o3f f3x demi(x3f) f3o o3o (F=ff) o3x x3f F3o f3f o3F f3x x3o

i.e. it also could be described as a diminished bistratic segment of ex, as ike || tet-dim-doe || id.
That tet-dim-doe (tetrahedrally diminished dodecahedron) in turn rasps 4 vertices of a doe (in tetrahedrally arrangement) down to the neighbouring vertices. Accordingly its faces are (fxxx) = fx&#x -trapezia and f3o triangles. Even so this medial section itself is not CRF (here: not Johnsonian), the total polychoron is CRF. The trapezia there happen to be according sections of the mibdies and the large regular triangles are sections of the teddies. The longer f-edges of that section in fact just occur as sections of the lacing pentagons.

Within the above lace city one vertex at the left end of the medial section is missing and every second vertex of that semiregular hexagon x3f. As this could be chosen in either of 2 alternating ways, this shows also the chirality. On the other hand it is known that the vertices of doe could be used for an inscribed chiral compound of 5 tets. One of these here has been selected for the diminishings. And in fact, the 4 missing vertices of that layer represent the centers of the teddies. While the centers of the 12 mibdies would represent a further layer, which in the above lace city was completely erased (when compared to that of ex).

The total count of cells of this CRF will be:
1 ike + 50 tets + 4 teddies + 12 mibdies + 1 id

Perhaps someone wants to render some nice pics of that polychoron?

--- rk

by **Klitzing** » Thu Feb 16, 2017 11:35 pm

... and then, there would be the possibility too, to diminish that fellow even further: to omit the opposite vertices of that already tetrahedrally diminished dodecahedronal section. That would make then a cubically diminished dodecahedronal section.

That is we could well consider: ike || cube-dim-doe || id, or in terms of lace cities either

Code: Select all: x3o o3f f3o o3x demi demi o3f (f3x) (x3f) f3o (F=ff) o3x x3f F3o f3f o3F f3x x3o

or alternatively that orientation

Code: Select all: o2x f2o x2f f2o o2x x2o o2F F2x o2F x2o (F=ff) (V=2f) o2o f2x x2F F2f Vo2oV F2f x2F f2x o2o

Again these diminishings at this layer will produce teddies. That is 8 in our new scenario. But this then would also further diminish the cells, which occured by the diminishings at the already fully omitted lower medial layer (the f-scaled icosahedral one). That is, the 12 mibdies there would become teddies too. - While the former 8 ones are vertical ones, these 12 now would be lying ones.

And, for sure, the count of remaining tetrahedra also decreases once more. In fact, the total count of cells now becomes:
1 ike,
20 teddies (J63),
30 tets,
1 id

And the overall directed axially chiral tetrahedral symmetry of the last time polychoron here would become a directed axially pyritohedral symmetry. And, for sure, that new polychoron is still a CRF!

--- rk

by **ndl** » Sun Jan 27, 2019 4:47 am

I don't have a fancy rendering program but here are some snapshots from Stella4D

Cube-Diminished:

: CubeDim Bistratic.JPG (66.58 KiB) Viewed 72953 times

by **ndl** » Sun Jan 27, 2019 4:49 am

Tetra-Diminished:

: TetraDim Bistratic.JPG (70.19 KiB) Viewed 72953 times

by **ndl** » Sun Jan 27, 2019 4:51 am

And the first Pyro-Diminished:

: Dim600.JPG (85.52 KiB) Viewed 72953 times

by **ndl** » Sun Jan 27, 2019 5:18 am

Another interesting thing to point out about quickfur's first diminishing, it's basically a pentagonal anti-prism ursachoron with an extra layer of vertices on top to make it CRF. I wonder if there are any more polyhedra that this can be done for?

by **Klitzing** » Sun Jan 27, 2019 2:37 pm

Wow, great stuff, ndt !!!
Now, nearly 30 months after their descriptive posts, those CRFs finally got rendered!

The according incmat files meanwhile are online awailable, for sure.
Those are, in the order of your pics: ike||cube-dim-doe||id, ike||tet-dim-doe||id, and doe||6-dim-id||f-ike||doe.

Within those renders the bottom/outermost cell surely never is being shown explicitely. But within the last render the next-to-outermost peppies also became omitted.

--- rk

by **ndl** » Mon Jan 28, 2019 4:03 am

Yes, stella4d by default hides the "front" cells in the projection.

by **ndl** » Sun Mar 03, 2019 4:18 am

Based on quickfur's first diminishing in this post, one could do the same thing with a mibdi or teddi in the middle, and 3 or 4 does. Meaning:

Mibdi || f-Mibdi || Metabipentadim-id || doe

or

teddi || f-teddi || tripentadim-id || doe

Also obviously this could be done with just single dim ike as well.

Here's a render of the teddi one:

: Teddi-dim ex.JPG (51.4 KiB) Viewed 72805 times

by **ndl** » Mon Mar 04, 2019 3:22 am

Alternatively, adding one more vertex for symmetry (for a total of 54), that above one could be described as a tetra doe-dim ex with add'l 14 vertices removed in the lining between the 4 does.

tet || pseudo inv f-tet || pseudo (f,x)-co || pseudo (x,f)-tut || pseudo (f,x)-tut || pseudo f-oct || inv tet

: Tetra Doe-Dim ex.JPG (46.16 KiB) Viewed 72797 times

by **Klitzing** » Tue Mar 05, 2019 1:16 pm

The first one looks to be the axial diminishing of ex down to the layers ike || f-ike || id || doe, which furthermore becomes tridiminished according to around-symmetry. Thus it could be spoken of as an "around-symmetrically tri-diminishing of a tetracontahexa-diminished hexacosachoron". The first part reduces to "arsted" within the according OBSA. For the latter part we have to detail the omitted layers of ex: .x.fo.o..3.o.ox.o..5.o.oo.x..&#xt - thus 46 = 1+20+12+12+1. So we could speak here of some dia-disdodeca-icosa-diminishing. Thus the total OBSA here might become "arsted diddidex".

Btw. cf. https://bendwavy.org/klitzing/explain/johnson.htm#axials and scroll down a bit. There you'll find already "arsted biscrox", a similar diminished rox, which further became around-symmetricaly tri-diminished. That one has been found already in 2016. (And probably is burried somewhere in this forum too.) - There I additionally introduced already OBSA-prefixes "arsd" (single diminishing), "arspabd" (parabidiminishing), "arsmabd" (metabidiminishing), and that "arsted" (tridiminishing).

The other one you brought up was given wrt. to the axial symmetry with tetrahedral around-symmetry, in fact it is x.o.o….o.x.fo3o.f.x....f.o.oo3o.o.f....x.f.ox&#xt - thus some 62=4+12+12+4+12+4+12+6-diminishing of ex, when simply considering the missing vertices. Obviously this becomes a bit clumbsy, if tried to convert directly into an OBSA, even without an "ars-…-d".

OTOH that one is not simply a tetra-doe-diminished ex, as your file name of the pic suggests. Rather its total cell count is 10 tets + 4 does + 6 mibdies + 8 teddies (not all of these are visible within your given front view). Thus you have in fact 4 deep diminishings (until the doe layer) plus 14=6+8 shallow diminishings (until the ike layer). So we might speak of some "hoddated ex" ((shallow-)hexa-octa-diminished deep-tetra-diminished hexacosachoron).

--- rk

by **ndl** » Wed Mar 20, 2019 1:44 am

I was analyzing doe-deep diminishings of ex and I found 4 different bidiminishings:

At antipodes (para?):
- No possible 3rd doe diminishings

Connected by face (meta?):
- Can have a 3rd doe connected to:
1 - para face
2 - meta face (can have 4th doe as well)
3 - vertex

Connected by vertex (?):
- Can have 3rd doe connected to para vertex (or face as mentioned)

Separated by pappy (ortho?):
- Can have 3rd doe in between (already mentioned above)

by **Klitzing** » Wed Mar 20, 2019 8:38 am

Well yes, that looks correct.

The doe-deep mono-diminished ex looks as lace city wrt. 5-fold perp symmetry:

Code: Select all: o5o o5o o5x x5o x5o o5o f5o o5f o5f o5x f5o f5o x5x o5o o5f o5f x5o f5o f5o o5f o5o o5x o5x x5o o5o o5o

or wrt. 3-fold perp-space symmetry

Code: Select all: o3o o3f f3x x3f f3o o3o f3o o3F F3o o3f o3x x3f F3o f3f o3F f3x x3o f3o o3F F3o o3f o3o o3f f3x x3f f3o o3o x3o o3f f3o o3x o3o

From those representations it becomes obvious that an alike second non-intersecting doe-deep diminishing can take place at the opposite vertex

Code: Select all: o5o o5o o5x x5o x5o f5o o5f o5f f5o f5o x5x o5f o5f f5o f5o o5f o5x o5x x5o o5o o5o

or at a vertex of the the one-but-last layer

Code: Select all: o5o o5o o5x x5o x5o o5o f5o o5f o5f o5x f5o f5o x5x o5f o5f f5o f5o o5f o5x x5o o5o

or at a vertex of the the two-but-last layer

Code: Select all: o3o o3f f3x x3f f3o o3o f3o o3F F3o o3f o3x x3f F3o f3f o3F f3x f3o o3F F3o o3o o3f f3x x3f x3o o3f f3o o3o

or at a vertex of the the three-but-last layer

Code: Select all: o5o o5o o5x x5o x5o o5o f5o o5f o5f o5x f5o f5o x5x o5o o5f o5f x5o f5o f5o o5f o5x

(An intersection at a vertex of the four-but-last layer (i.e. equatorial layer) would not be visualizable with 5-fold nor 3-fold perp space symmetry. But it would be possible with 2-fold perp space symmetry. None-the-less that one would come out to be already intersecting. Thus it is not of interest here, in the context of CRF.)

--- rk

by **mr_e_man** » Tue Oct 25, 2022 5:42 pm

How about rendering the 600-cell lunae?

by **quickfur** » Tue Oct 25, 2022 6:52 pm

mr_e_man wrote:How about rendering the 600-cell lunae?

I've already done those, but they're buried somewhere in the original 4D CRF thread which got split into multiple smaller threads, so you might have to do a little digging to find them.

by **mr_e_man** » Wed Oct 26, 2022 1:21 am

Excavation successful:
viewtopic.php?f=25&t=1468&start=420#p17873 (pictures)
viewtopic.php?f=32&t=1468&start=510#p18335 (discussion & naming, on through the next page)
viewtopic.php?f=32&t=1927&start=240#p20524
http://hi.gher.space/wiki/CRFP4DP/Dimin ... _600-cells

by **mr_e_man** » Wed Oct 26, 2022 3:14 am

Wait... Are there other lunae you haven't considered? Or would they be non-CRF?

You describe a bisection of the 600-cell by the vertex orthogonal to the cutting (hyper)plane; i.e. the normal vector. So a luna is described by two vertices. A view of the 600-cell centred on one vertex shows the vertices arranged symmetrically in groups, in increasing distance from the first vertex:

1 + 12 + 20 + 12 + 30 + 12 + 20 + 12 + 1

(Of course each group of vertices forms an ike or doe or id.)

You only considered the second vertex as being in one of the groups of size 12. What if the second vertex is in one of the groups of size 20 or 30?

by **mr_e_man** » Wed Oct 26, 2022 2:36 pm

Well, there was some study of the 1/6 and 2/6 lunae of the 600-cell (where the second vertex is in a group of size 20):

viewtopic.php?f=32&t=1948
https://bendwavy.org/klitzing/explain/johnson.htm#luna

But I don't see anything about the 1/4 luna of the 600-cell (where the second vertex is in the group of size 30, orthogonal to the first vertex).

I think this luna would have a bisected id with o2o symmetry; this is not regular-faced. Maybe replacing this with a bilbiro could make it CRF. One vertex of the bilbiro would be at the centre of the 600-cell.

Hi.gher. Space

Interesting 600-cell diminishings

Interesting 600-cell diminishings

Re: A 600-cell diminishing

Re: A 600-cell diminishing

Re: A 600-cell diminishing

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Re: Interesting 600-cell diminishings

Who is online