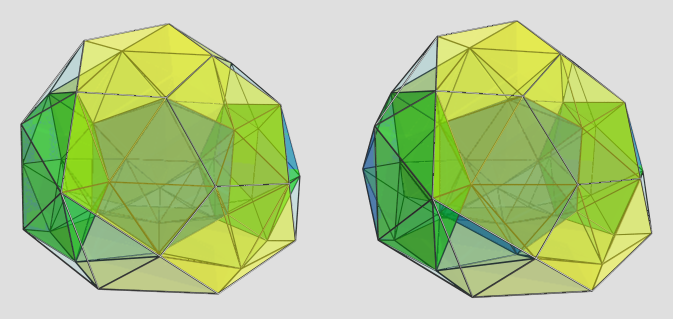
This sets the basic structure of this CRF. After that, I looked around the result a bit to see what else can be diminished to yield a more-or-less symmetrical structure. Around the pentagonal antiprism, it looked like deleting a circle of 10 vertices would produce a ring of teddies (tridiminished icosahedra) around it in alternating orientation. Furthermore, another 10 vertices can be deleted above 10 of the faces of the middle dodecahedron (where they are not shared with the adjacent dodecahedra), yielding two adjacent rings of icosahedral wedges (metabidiminished icosahedra) that encircle the two pentagonal faces shared between the middle dodecahedron and the two adjacent dodecahedra. The remaining gaps are filled by an alternating ring of 10 tetrahedra connected by their vertices. Each tetrahedron shares an edge with a great circle of edges that lies orthogonal to the plane of the 3-dodecahedron + antiprism ring.
The overall shape is a kind of blunt wedge, or trapezoidal shape with pentagonal symmetry. Here are some projections of it:
Side-view, showing the blunt-wedge shape:
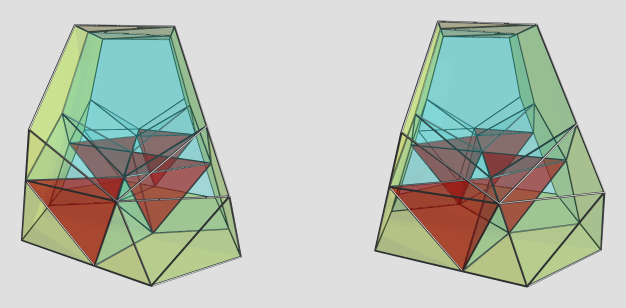
The "blunt edge" of the shape (projected to the top here) is the pentagonal antiprism; the other 3 sides are the 3 dodecahedra. The metabidiminished icosahedra lie between the red tetrahedra. There are actually 6 tetrahedra visible in this projection, but for clarity I didn't color the two that lie on the limb of the projection (they are at 90° to the 4D viewpoint). The far side of the polytope has the same structure but in skewed orientation, making a total of 10 tetrahedra.
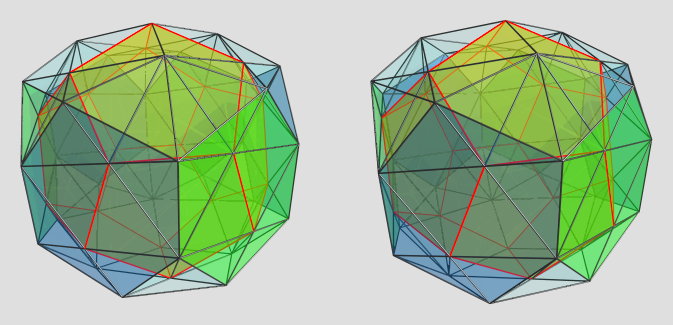
Projection centered on middle dodecahedron:
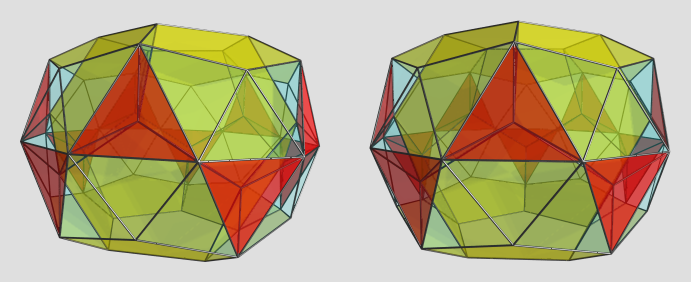
The big yellow dodecahedron is the one in the center. You can see parts of the other two dodecahedra as yellow pentagons on the top and bottom. The metabidiminished icosahedra are clearly seen, and the edges around outer faces of the tetrahedra trace out the bottom of the teddies that lie on the far side of the polytope from this viewpoint.
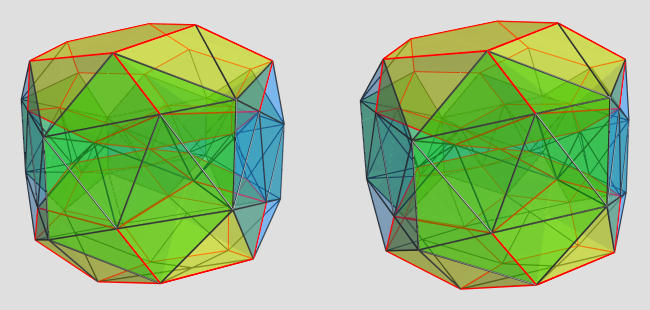
Projection centered on pentagonal antiprism:
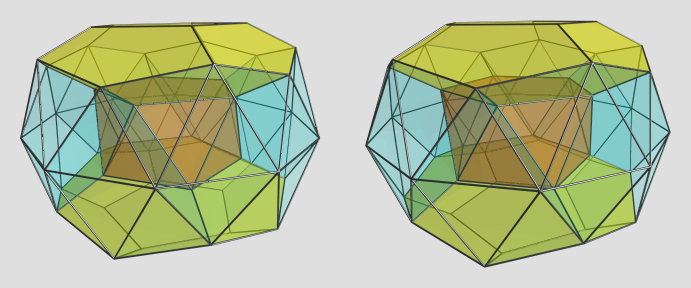
Here we see the pentagonal antiprism sandwiched between the other two dodecahedra. If you look carefully, you can see teddies attached to each of the triangular faces of the antiprism, with their bottoms pointing outwards.
This polytope has 60 vertices, 170 edges, 144 faces (100 triangles, 44 pentagons), and 34 cells (10 tetrahedra, 10 metabidiminished icosahedra, 10 tridiminished icosahedra, 3 dodecahedra, and 1 pentagonal antiprism).
Here are the coordinates of the 60 vertices (scaled such that the edge length is 2):
- Code: Select all
# phi = (1+sqrt(5))/2 = golden ratio
<0, 0, ±2*phi, 0>
<0, ±2*phi, 0, 0>
<0, ±1, ±phi, -phi^2>
<0, ±phi, ±phi^2, -1>
<0, ±phi^2, ±1, phi>
<±1, 0, ±phi^2, phi>
<±1, ±phi, 0, -phi^2>
<±1, ±phi^2, ±phi, 0>
<-phi, 0, 1, -phi^2>
<phi, 0, -1, -phi^2>
<-phi, ±1, phi^2, 0>
<phi, ±1, -phi^2, 0>
<±phi, ±phi^2, 0, -1>
<-phi^2, 0, phi, -1>
<phi^2, 0, -phi, -1>
<±phi^2, ±1, 0, phi>
<-phi^2, ±phi, 1, 0>
<phi^2, ±phi, -1, 0>
<±phi, ±phi, ±phi, phi>